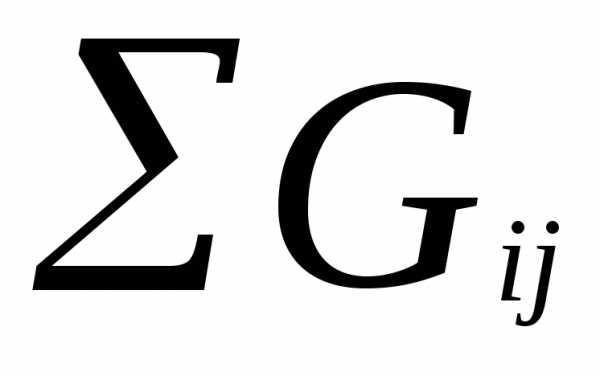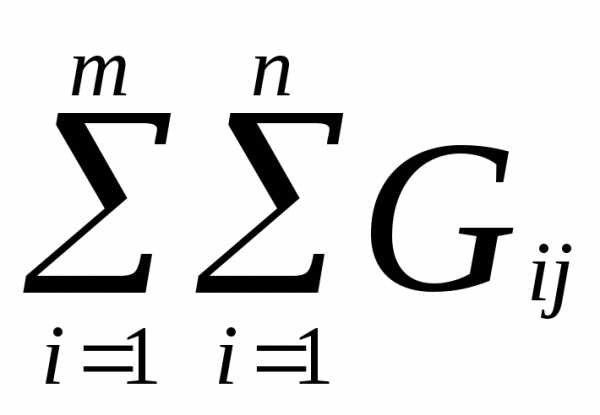Расчет весовых коэффициентов в сравнительном подходе

---

 Согласно требованиям ФСО, контролирующих органов необходимо производить обоснование всех расчетов и результатов в отчете по оценке. В настоящее время практически отсутствуют методики обоснования весовых коэффициентов в сравнительном подходе. Есть общие формулировки, что необходимо присваивать вес каждому аналогу в зависимости от произведенных корректировок, но при этом отсутствует конкретная информация как это сделать. В данной статье автор предлагает вариант распределения весовых коэффициентов, достаточно простым обоснованным способом. Описываемый в статье вариант определения весовых коэффициентов предлагается для метода прямого поэлементного сравнения аналогов с объектом оценки.

Обычно в сравнительном подходе составляется сравнительная таблица аналогов, где проставляют корректировки по различным параметрам рассчитанные тем или иным способом (уже на основании рыночных данных). В результате по каждому аналогу образуется сумма корректировок, которая может быть больше, меньше или равна нулю. На этом этапе Оценщику необходимо распределить веса по каждому аналогу в зависимости от внесенных корректировок по ним и обосновать их согласно ФСО.

Зачастую Оценщики прибегают к экспертному распределению весов с приведением, каких либо оснований.

Данную процедуру можно упростить, применив математический способ расчета весовых коэффициентов. Для этого необходимо рассчитать параметр, обратный удельному весу суммы корректировок по каждому аналогу в общей сумме корректировок аналогов (чем больше удельный вес, тем меньше весовой коэффициент и наоборот). Производить расчет предлагается по следующей формуле:

 

Очевидно, что  не линейная, иначе распределение весов было бы гораздо проще по прямой пропорции.

Рассмотрим пример расчета с использованием формулы (2),

	аналог 1	аналог 2	аналог 3	сумма
сумма корректировок	1	0	0	1
вес	20%	40%	40%	100%

Распределение весов показывает, что при двух стопроцентно идентичных аналогов оцениваемому объекту, первому аналогу с минимальной корректировкой присвоен вес в 20% и разница с другими аналогами составляет также 20%.

	аналог 1	аналог 2	аналог 3	сумма
сумма корректировок	11	10	10	31
Вес	31%	34%	34%	100%

В другом случае, различие в корректировках в 1 единицу дает разницу в 3% в весах. Это говорит о том, что аналоги, имеющие большую величину сумм корректировок одинаково плохи, и разница в весах между ними соответственно невелика.

Графически зависимость веса от суммы корректировок (при нулевых корректировках для трех аналогов) выглядит так,

 

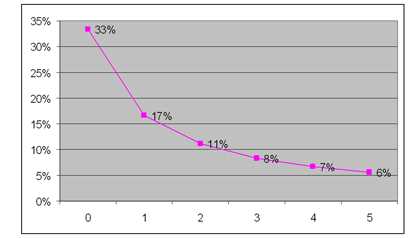
Из графика видно, что чем больше корректировка, тем меньше ее вес и при увеличении величин корректировок разница в весах снижается. Вид графика функции не меняется от величины корректировок.

Известно также, что величины корректировок могут быть как положительные, так и отрицательные, поэтому параметр S берется по модулю, так как значения корректировок, например -1 и +1 равнозначны. В случае, когда сумма корректировок (S) равна нулю, в формулу введен минимальный параметр 1, который дает определять вес при нулевых значениях сумм корректировок и избежать математической ошибки деления на ноль.

Таким образом, предлагаемая формула, по мнению автора, наиболее близко к истине объясняет распределение весов в зависимости от сумм корректировок по аналогам.

Приведенная формула была написана для сравнительного подхода при распределении весов по аналогам. Однако ее также можно применять и в других областях, где применяются аналогичные приемы расчетов.

 

Слепцов Сергей Валентинович

Член РОО

www.top-ocenka.com

Весовой коэффициент

Весовым коэффициентом называется число или степень числа, которая выражает значимость определенного предмета или явления. Например, оценивая перспективы вложения средств, инвестор анализирует различные экономические факторы и распределяет их по степени значимости. У наиболее значимого фактора будет самый высокий весовой коэффициент. Расчет весового коэффициента какого-либо явления может производиться только при наличии других явлений, с которыми оно будет сравниваться.

Значение весового коэффициента в экономической науке

Первое значение весового коэффициента состоит в его влиянии на целеполагание и финансовое планирование. Если у человека есть выбор между различными моделями поведения в финансовой сфере, он должен выбирать ту, весовой коэффициент аргументов которой больше, чем у других.

Второе значение – определение весового коэффициента позволяет составить прогноз о том, что произойдет в исследуемой области вследствие того или иного явления. Вероятнее всего будет происходить то событие, у составляющих (аргументов) которого больший весовой коэффициент. На основании прогнозов вырабатывается план действий, что особенно часто наблюдается в макроэкономике (экономические отношения на внутригосударственном и международном уровнях).

Третье значение – весовые коэффициенты обязательно используются при создании компании, которая нуждается в инвестиционной поддержке. Когда предприниматель обратится к инвесторам за помощью, он перечислит им причины, по которым стоит вкладывать деньги в его компанию, у каждой причины будет свой весовой коэффициент. Чем больше будет суммарное значение весового коэффициента, тем выше вероятность получения предпринимателем инвестиционной поддержки.

Четвертое значение – расчет весового коэффициента может быть подвержен изменениям с течением времени, по изменениям можно судить о переустройстве экономической системы. Ведь весовой коэффициент определенного фактора может повышаться или понижаться только в том случае, если будет расти или падать значимость других факторов, а это может происходить только в случае преобразований в экономике.

utmagazine.ru

Методы определения весовых коэффициентов.

Прием 1.

Для каждого частного критерия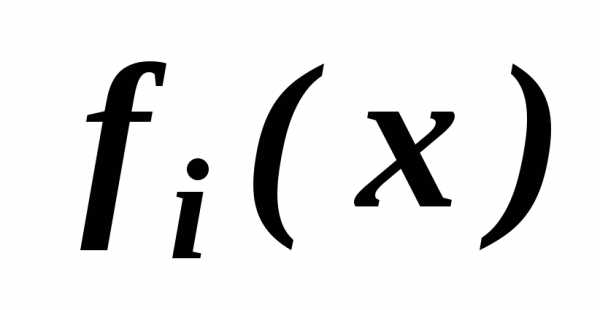

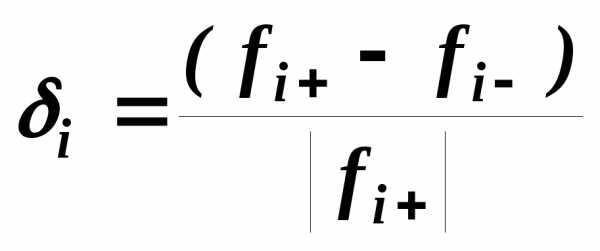
вычисляется коэффициент относительного разброса:

( 11.2.0 )

где

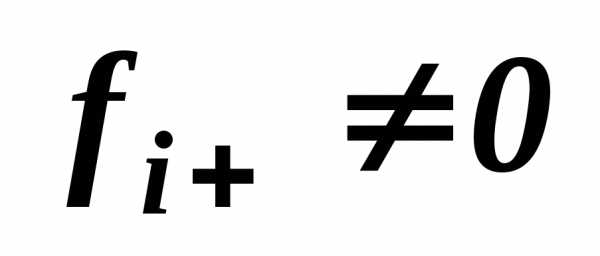, иначе прием 1 применять нельзя.

Для того, чтобы вычислить необходимо решить соответствующие задачи однокритериальной оптимизации. Не всегда это удается, поэтому в формуле ( 11.2 .0 ) допустимо использование оценок этих величин. Далее весовые коэффициенты вычисляются по формуле

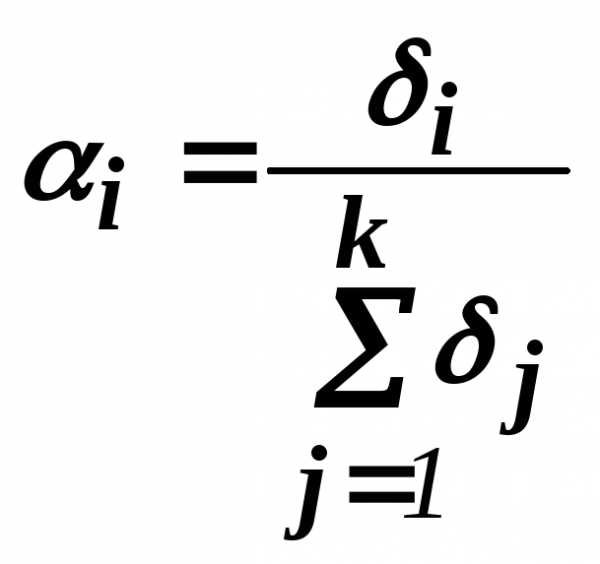(11.2.0 )

При таком подходе в обобщенном критерии «большой вес» имеют те критерии, у которых минимальное значение частного критерия сильно разнится от максимального. Действительно, если 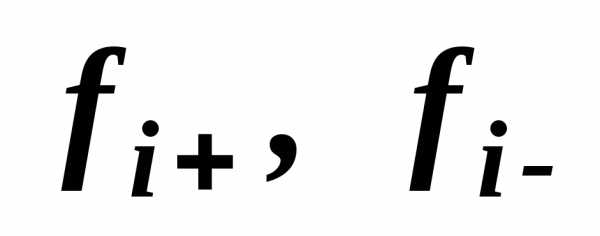— близки, то при любом

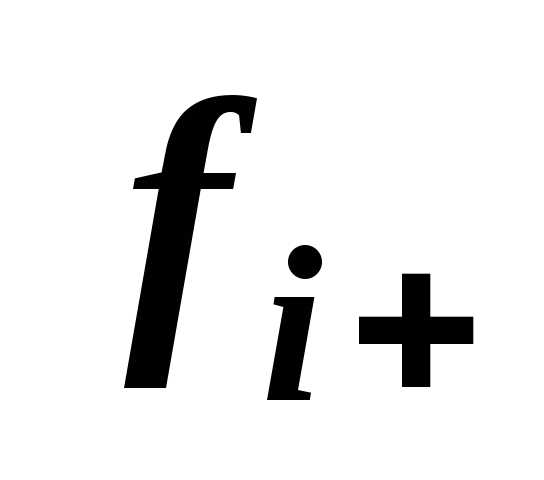полученное решение будет близко к. И, наоборот, чем больший разброс имеет некоторый критерий , тем с большим весом его необходимо взять в линейной свертке. В предельном случае, когда

, то есть такой критерий не следует включать в обобщенный.

Вернемся к примеру ( 11.1 .0 ) и применим к нему прием 1 :

Выше для этого примера мы получили общий вид решения:

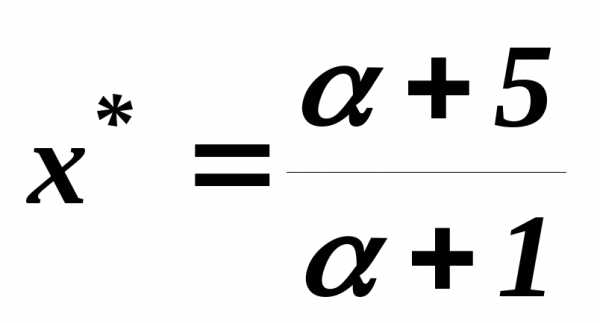в зависимости от .

Наконец получаем: .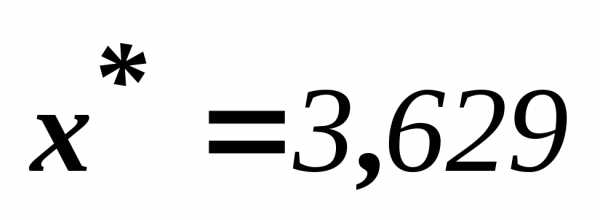

Получили одну из эффективных точек для задачи ( 11.1 .0 ).

Замечание 1.

Следует обратить внимание на то, что при таком подходе «важность» критерия полностью определяется поведением функции

на области.

Прием 2.

Может применяться при условии 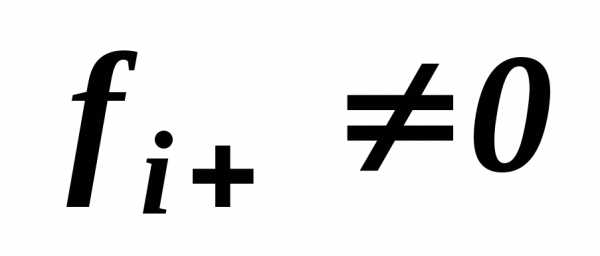. Вводятся в рассмотрение вспомогательные функции:

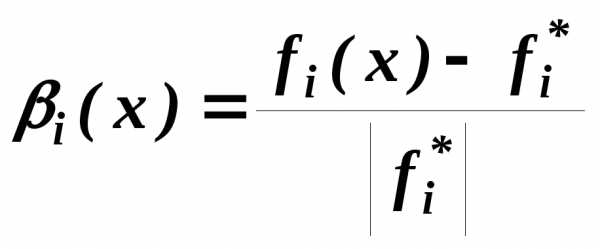
которые можно рассматривать как относительное отклонение частного критерия от его наименьшего значения.

Важность 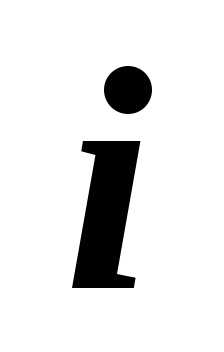— го критерия определяется через неравенство:

, где 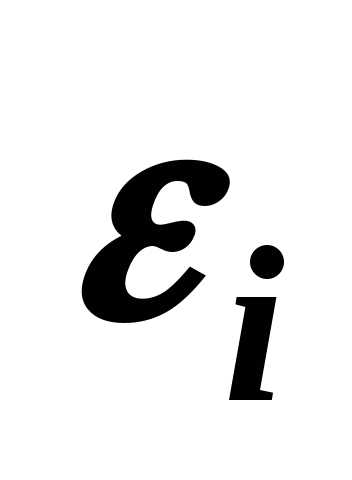задает постановщик задачи:

чем важнее критерий, тем меньше 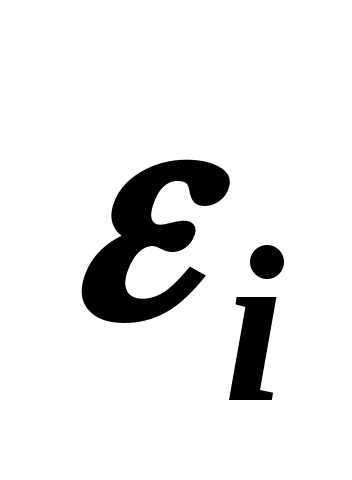. Затем для каждого критерия вычисляется радиус шара , имеющего

центром , являющуюся решением задачи:

,

внутри которого выполняются условия: .

Далее вычисляются по формуле:

.

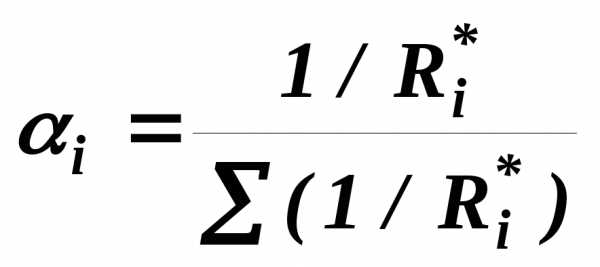При таком подходе важность критерия определяется двумя факторами:

Это является бесспорным достоинством метода. Проиллюстрируем на нашем примере ( 11.1 .0 ):

Назначим .

На этом этапе мы не даем ни одному из двух критериев никакого предпочтения.

.

В результате получили, что 1-й критерий оказался важнее 2-го.

Замечание.

Приемы 1, 2 имеют довольно ограниченное применение , так как в силу необходимости решения целой серии однокритериальных задач, кроме того определяющим является вид функции .

Прием 3. Использование попарных приоритетов.

В продолжение последнего замечания следует отметить, что часто не вид функции является решающим в определении важности критериев, а сама сущность проблемы, то есть степень важности одного критерия по сравнению с другим определяется не из математической постановки задачи ( 11.1 .0 ), а путем привлечения дополнительной информации.

Наиболее приемлемым подходом является попарное сравнение критериев по важности в количественном выражении.

Попарное сравнивание критериев по предпочтению между собой должно быть выражено числовыми оценками 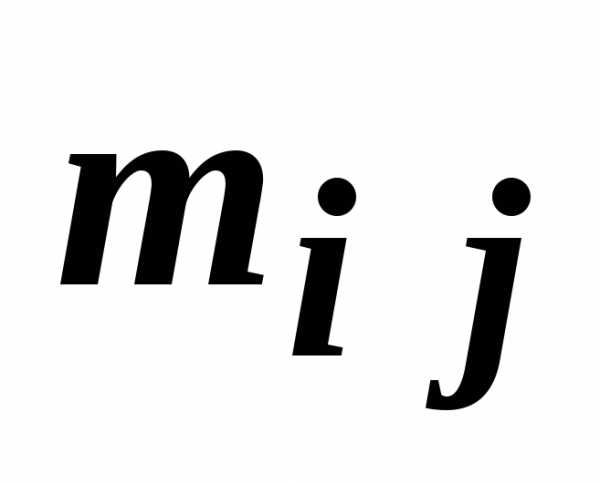в виде обыкновенной дроби. Например,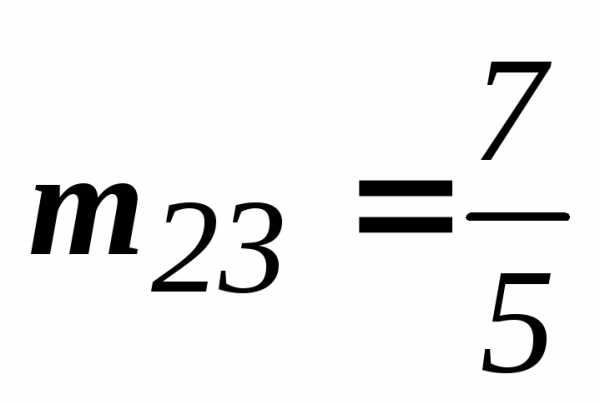означает, что второй критерий «важнее» третьего враза , а третий критерий «менее важен» второго тоже в раза .

По имеющейся информации о степени предпочтения, по важности каждой пары частных критериев составляется матрица размерности, где

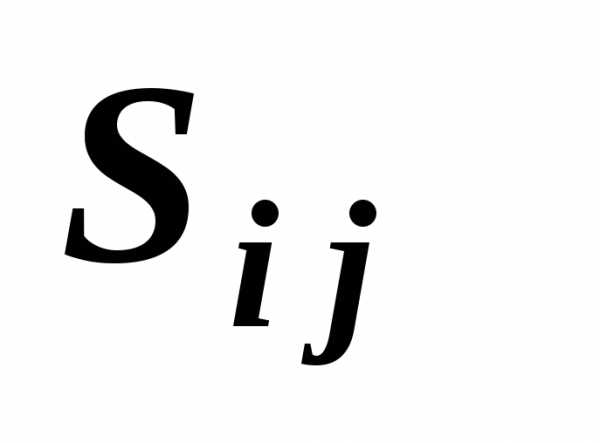равно числителю

равно знаменателю

Например, имеем трехкритериальную задачу, причем выяснили, что первый критерий важнее второго, третий критерий важнее второго, первый важнее третьего. В нашем случае первый критерий важнее третьего и второго, то есть следует ожидать, что наибольшим будет .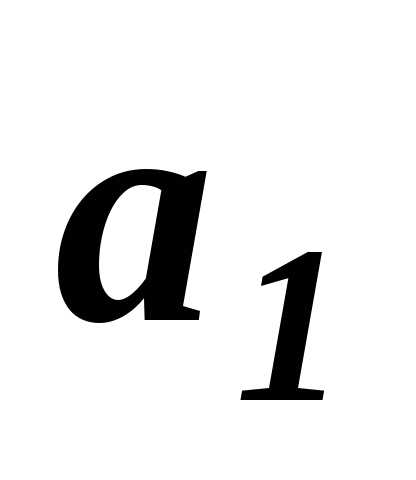

Зададимся конкретными данными:

.

.

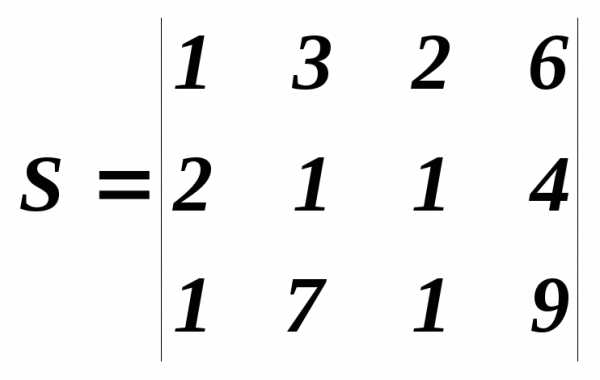
Вопреки ожиданиям, наибольшим получили .

Дело в том, что здесь сыграли роль именно количественные показатели:

третий критерий важнее второго в раз. При определении надо быть очень внимательным. Например, для 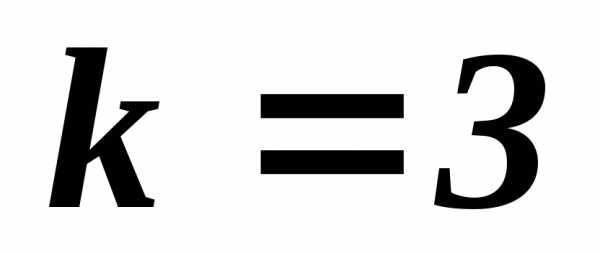, если мы четко знаем, что самым важным является первый критерий, затем второй, и, наконец, третий, то для определенияданным приемом можно воспользоваться, нодолжны в этом случае удовлетворять условиям: .

Вернемся к нашему примеру ( 11.1 .0 ) и представим в виде таблицы решения, полученные с помощью линейной свертки, применяя прием 3 при различных .

Прием 4. Использование интервальной информации.

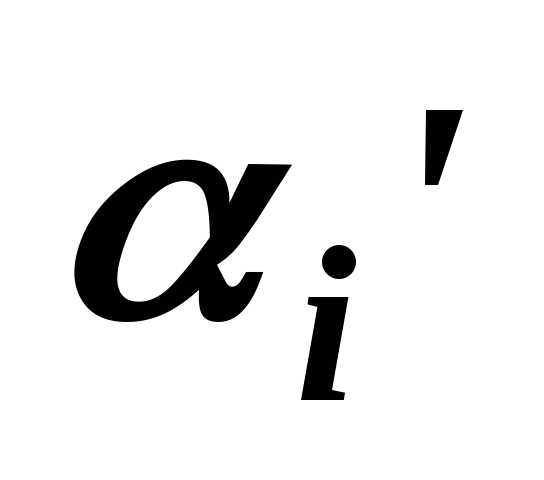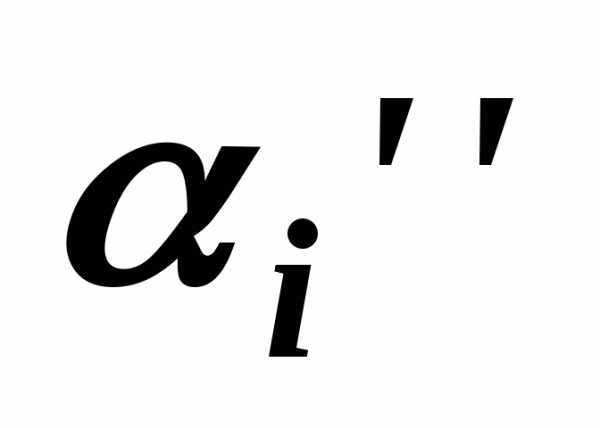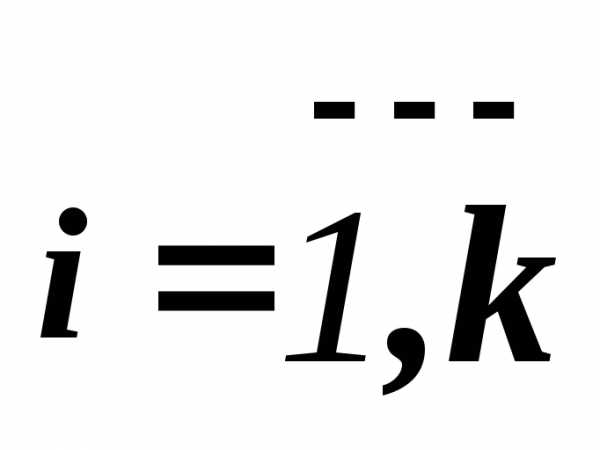Одним из подходов, наиболее отвечающим практике, является интервальное задание весовых коэффициентов , то есть задание,,, где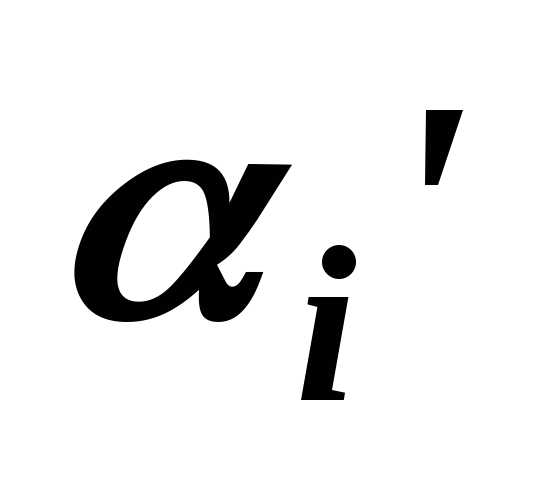,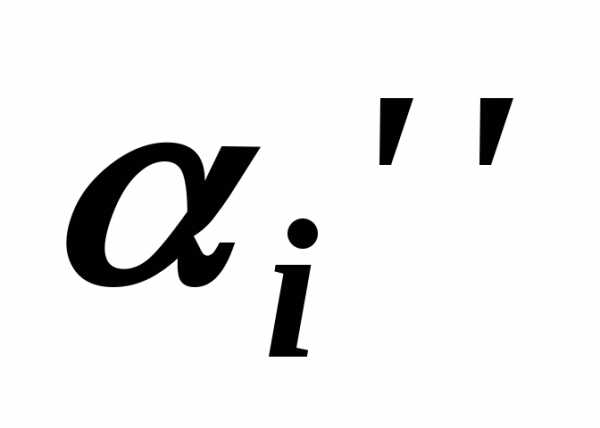— соответственно нижняя и верхняя граница для:.

С постановочной точки зрения этот подход предпочтительнее предыдущих.

Математически он приводит к решению следующей однокритериальной задачи с 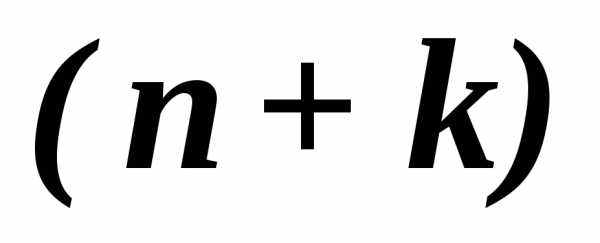переменными:

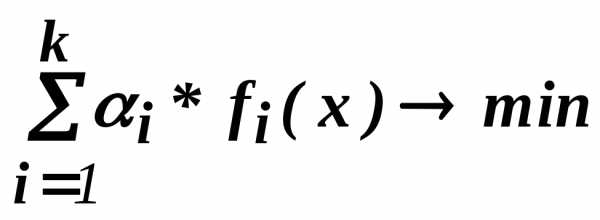
В качестве примера снова рассмотрим задачу ( 11.1 .0 ) при условиях :

Для этого необходимо решить такую задачу:

Такую задачу пришлось решать численно и получено:

Замечание.

Как и в предыдущих приемах , в общем случае, гарантий того, что получено эффективное решение, нет .

Прием 5. Теоретико-игровая модель выбора весовых коэффициентов.

В этом способе выбора весовых коэффициентов используют элементы матрицы :

где

— точка оптимума — того частного критерия.

Значения характеризуют влияние решенияна частный критерий.

Очевидно, что

, а

поскольку мы берем по абсолютной величине.

Строится матрица , она будет квадратной:

Эту матрицу рассматривают как матрицу платежей в игре двух лиц с нулевой суммой.

Каждой строке соответствуют оптимальные решения по каждому частному критерию, а столбцам соответствуют оптимальные значения частных критериев оптимальности.

Партию игры можно представить следующим образом:

первый игрок может выбрать одну из чистых стратегий , а второй игрок выбирает одну из чистых стратегий.

В этой игре «maxmin» равен 0, а «minmax» равен

то есть игра не имеет седловой точки.

Это означает, что оптимальное решение игры следует искать в форме смешанных стратегий, то есть:

для первого игрока каждая стратегия

выбирается с вероятностью ,

выбирается с вероятностью ,

…………………………………………………..

выбирается с вероятностью

.

Для второго игрока с вероятностями

выбирается с вероятностью ,

выбирается с вероятностью ,

…………………………………………………..

выбирается с вероятностью

.

Смешанная стратегия второго игрока может быть найдена из решения задачи линейного программирования, представленной в виде:

Решая эту задачу и получив значения находят значения:

.

В качестве примера снова рассмотрим задачу ( 11.1 .0 ):

Матрица принимает вид:

Решаем задачу вида:

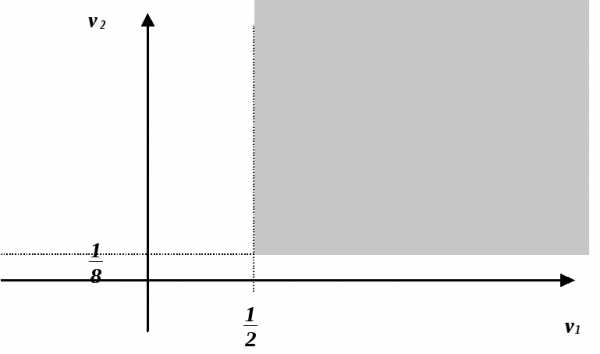
Графически решая ее получаем:

,

Следовательно:

Прием 6. Определение весовых коэффициентов по разности максимального и минимального элемента матрицы .

— это матрица предпочтений.

Используется матрица , построенная по алгоритму, изложенному в приеме 5.

где

Вычисляются:

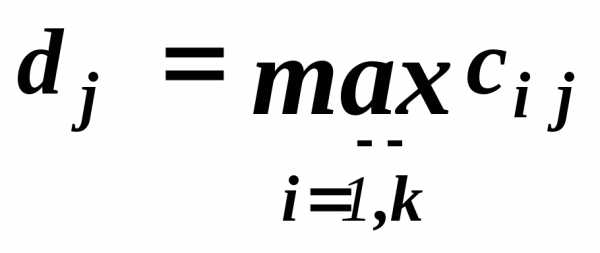
Далее вычисляются:

Значения таким образом вычисляют по формуле:

.

Вернемся к примеру ( 11.1 .0 ) и применим к нему прием 6 :

Матрица принимает вид:

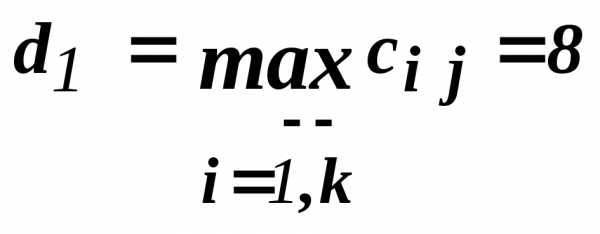
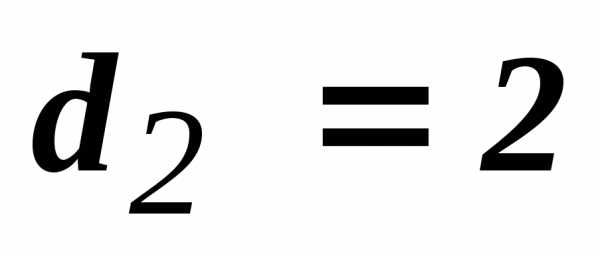
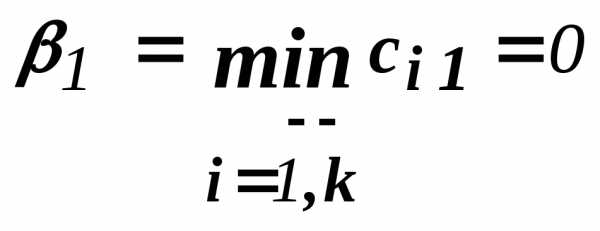
Далее:

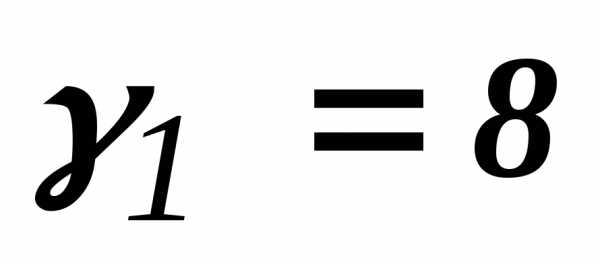
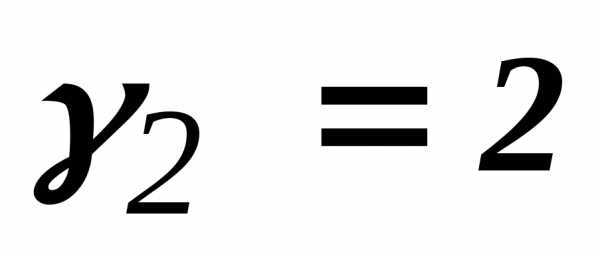
Следовательно:

Прием 7. Определение весовых коэффициентов при одинаковом приоритете частных критериев.

В этом способе выбора весовых коэффициентов определяется по формуле:

критерии равноправны.

studfiles.net

Весовые коэффициенты при расчете взвешенной скользящей средней

Скользящая средняя является одним из самых востребованных индикаторов в системах технического анализа: она чаще остальных используется в различных торговых системах и стратегиях. Существует несколько алгоритмов усреднения: простое среднее арифметическое и более сложные, такие как взвешенное скользящее среднее. Каждый из механизмов расчета даёт на выходе близкие, но всё же отличающиеся результаты. Тому, как эти незначительные отличия могут быть с успехом использованы трейдером в построении успешной торговой стратегии и посвящена данная статья.

Назначение скользящих средних

Многие популярные аналитические инструменты используют в работе усреднение данных в определённом временном периоде, а значит – полагаются на методологию расчета скользящей средней, так же известной как Mooving Average (MA). Сам индикатор отлично зарекомендовал себя как инструмент для определения направления тренда:

• если текущий уровень котировок выше, чем усреднённые значения цен за определённый период — имеется тенденция к росту;
• в обратной ситуации, когда цена котируется ниже, чем усредненное значение стоимости актива, можно говорить о наличии нисходящей тенденции.

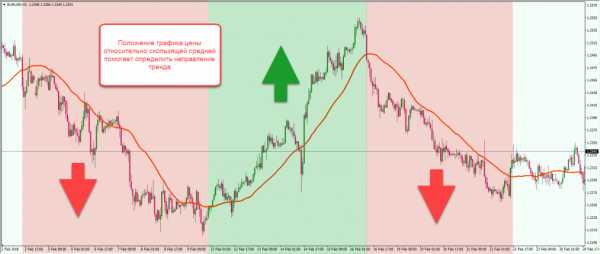
В трейдинге используется несколько методов усреднения исходных данных. Самый понятный из них представляет собой стандартный алгоритм расчета среднеарифметических значений, знакомый трейдерам со школьной скамьи. Этот метод позволяет получить простую скользящую среднюю, сложив цены закрытия каждой свечи внутри временного ряда заданной длины и поделив сумму на количество свечей в ряду (периоде). Схожим образом производится расчет экспоненциальных (EMA) и взвешенных (WMA) скользящих средних, но в этом случае алгоритм заслуживает отдельного пояснения, поскольку имеет ряд отличий.

Этапы вычисления среднего значения

Определение периода

Первым и общим параметром для всех типов расчетов скользящих средних является период. Он указывает, какое количество баров, начиная от последнего, будет участвовать в вычислении значения скользящей средней. «Скользящая» средняя получила свое название именно благодаря постоянному смещению области свечей, участвующих в расчете: появление каждого нового элемента графика приводит к сдвигу интервала сглаживания на 1 бар вправо.

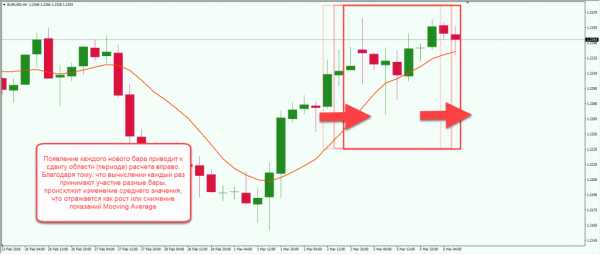
Этот принцип расчета периода используется во всех реализациях индикатора MA: взвешенных, экспоненциальных, сглаженных и простых.

Расчет средних значений скользящей

Чтобы определить среднее значение цены в периоде, в самом простом случае, необходимо найти среднеарифметическую величину по формуле:

где:

• SMA – простая скользящая средняя;
• P – цена каждого бара в периоде;
• N – период.

При простом расчете каждое значение цены внутри периода имеет одинаковый вес, что сказывается на графическом представлении индикатора – он становится менее чувствительным к сильным моментальным изменениям. Такая особенность приводит к запаздыванию реакции индикатора на начало тенденции, что не позволяет определить оптимальный момент для открытия и закрытия сделок. Алгоритм усреднения, при одинаковых весовых коэффициентах, не позволяет отфильтровать рыночный «шум» — незначительные колебания графика и линия SMA выглядит менее сглаженной.

Чтобы индикатор стал более информативным и чутко реагировал на сильное изменение рыночных условий, используется другой механизм усреднения – метод взвешенной скользящей средней.

Роль весовых коэффициентов

Величина вклада каждого значения из расчета простой скользящей средней может быть представлена в виде гистограммы:

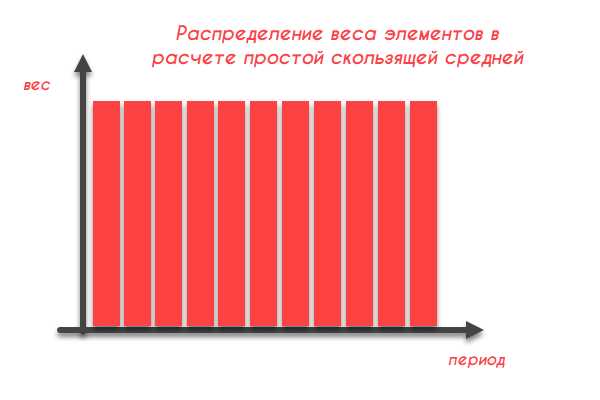
Здесь каждый элемент внутри периода имеет одинаковый вес с остальными, указывая, что для изменения усреднённой величины нужно очень сильное ценовое движение.

Чтобы повысить чувствительность необходимо снизить влияние первых свечей, и увеличить влияние последних элементов периода. Такой алгоритм позволит получить взвешенную скользящую среднюю, для которой значительные изменения котировок вызовут более быструю реакцию. Учёт влияния веса позволяет избежать ещё одного недостатка простой MA – чувствительность к «шуму»: незначительные ценовые колебания будут отфильтрованы расчетом, так как их абсолютная величина окажется близкой к средней величине, и они окажут меньшее влияние на изменение кривой скользящей средней.

Графическое представление распределения весов при расчете взвешенных скользящих средних представлено на следующем изображении:

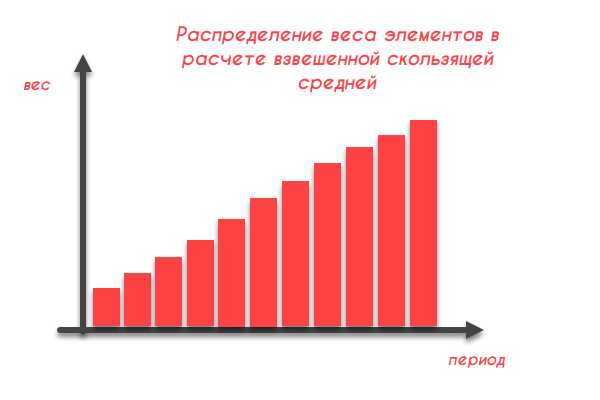
Алгоритм расчета взвешенной средней

Формула для определения величины взвешенной скользящей средней (WMA) имеет следующий вид:

здесь:

• WMA – взвешенная MA;
• N – период для расчета средних значений;
• W – удельный весовой коэффициент.

Принцип, позволяющий определить вклад весовых коэффициентов в расчет проще всего пояснить на примере. Если допустить, что требуется вычислить WMA для периода 15, то общий вес всех свечей будет равен единице (в абсолютном выражении – как сумма всех чисел ряда от 1 до 15), но вклады каждого из элементов окажутся неодинаковыми:

• вес первых трёх свечей в периоде составит: (1+2+3)/105 = 0,06;
• вес последних трёх значительно возрастёт: (13+14+15)/105 = 0,4.

Изменение котировки на один пункт относительно средней величины для последней свечи в периоде (это та свеча, что формируется в данный момент) оказывается более значимым для расчета, чем изменения, которые имели место в начале периода.

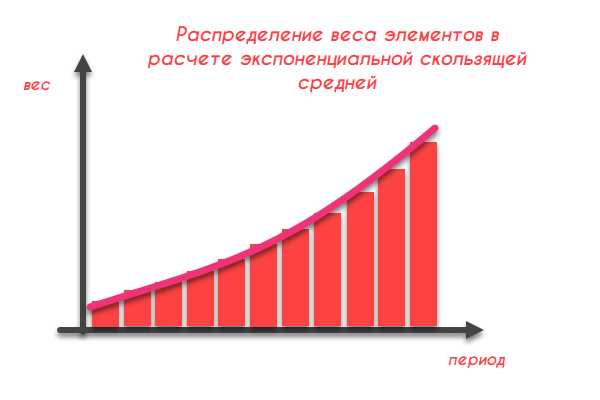
Экспоненциальное усреднение

В рассматриваемом выше примере распределение весовых коэффициентов имеет линейную зависимость от времени (периода), что подтверждается математически. В большинстве терминалов трейдерам доступен и частный случай – экспоненциальная версия Mooving Average, где, как следует из названия, распределение весов носит экспоненциальный характер.

Можно рассчитать все три рассматриваемых типа скользящих и убедиться в том, что при одинаковых исходных данных результаты не равны, но проще наложить эти кривые на график и сравнить достоинства и недостатки каждого способа усреднения.

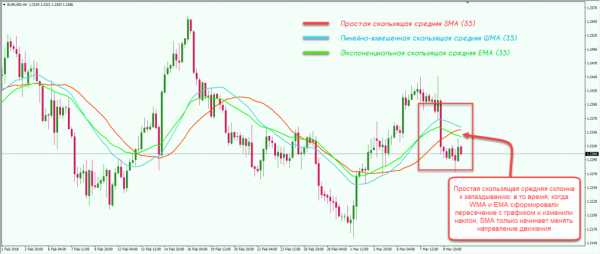
Из представленного графика видно, что линейно-взвешенный и экспоненциальный индикаторы обладают значительно меньшим запаздыванием относительно простого (SMA). Кривые, которые были рассчитаны с учетом весовых коэффициентов, на коротких отрезках получаются более сглаженными, резкие изменения цены оказывают меньшее влияние на общий результат расчета. WMA и EMA острее улавливают начало тенденций, но формируют больше точек пересечения с графиком.

Высокая подвижность взвешенных индикаторов приводит к тому, что источником более качественных торговых сигналов является простая скользящая средняя, что нивелируется значительным отставанием SMA от тренда, и в итоге не позволяет получить на выходе высокую эффективность торговой системы при опоре только на одну скользящую среднюю.

Использование в торговых системах

Для получения достоверных торговых рекомендуется использование большого количества индикаторов – до пяти WMA или EMA с различными параметрами периода. В таких стратегиях источником сигналов к входу в рынок выступает самый быстрый индикатор, по факту пересечения которого с другими линиями и принимают решения об открытии или закрытии сделок. В предложенном варианте стратегии используется 5 индикаторов:

1. Быстрая сигнальная линия WMA (8) – следует за графиком цены (красная).
2. Первое подтверждение WMA (20) – голубая.
3. Второе подтверждение WMA (35) – зелёная.
4. Среднесрочный тренд – WMA (50) – оранжевая.
5. Долгосрочный тренд – WMA(150) – синяя.

Вход осуществляется, когда сигнальная красная линия с периодом (8) осуществит последовательный пробой линий первого и второго подтверждения. В это время, оранжевая и синяя кривые должны указывать на направление тренда, совпадающие с направлением открытия сделки.

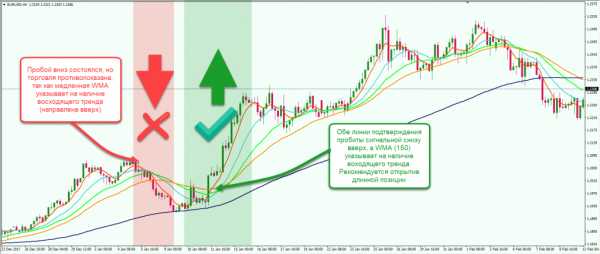
Использование весовых коэффициентов при расчете взвешенной скользящей средней позволяет получить отличные показатели доходности торговой системы благодаря значительному увеличению чувствительности индикатора. Вместе с тем, применение алгоритма усреднения с большим весом последних свечей в периоде приводит к формированию большого количества ложных пересечений, что требует внимательной настройки параметров остальных индикаторов для качественной фильтрации поступающих данных.

fx-invest.biz

Определение весовых коэффициентов показателей качества

Способ ранжирования. Эксперта просят расположить объекты экспертизы в порядке их предпочтения. Место, занятое при такой расстановке в ранжированном ряду, называется рангом. Значения весовых коэффициентов в таком случае рассчитывается по формуле:

,

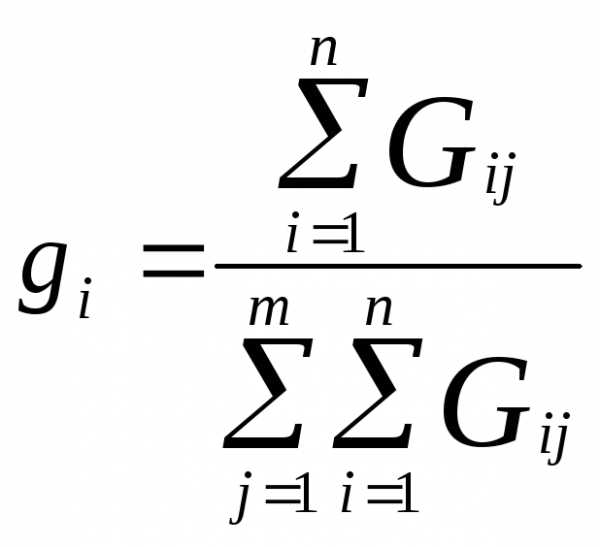где G_i,j– балл (ранг)j-го показателя, проставленныйi-м экспертом;n– количество экспертов,m– количество «взвешиваемых» показателей.

Способ попарного сопоставления. При этом способе эксперт получает таблицу, в которой по вертикали и горизонтали проставлены номера объектов экспертизы (показателей качества). Эксперту необходимо проставить в каждой клетке, относящейся к двум сравниваемым объектам (показателям), номер того объекта (показателя), который он считает наиболее важным. При попарном сопоставлении используется только верхняя часть таблицы. Расчет весовых коэффициентов производится по формуле:

,

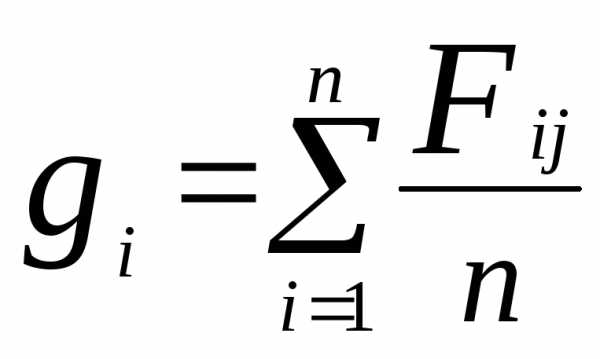где F_ij – частота предпочтенийi-м экспертомj—го объекта экспертизы, определяемая как:

,

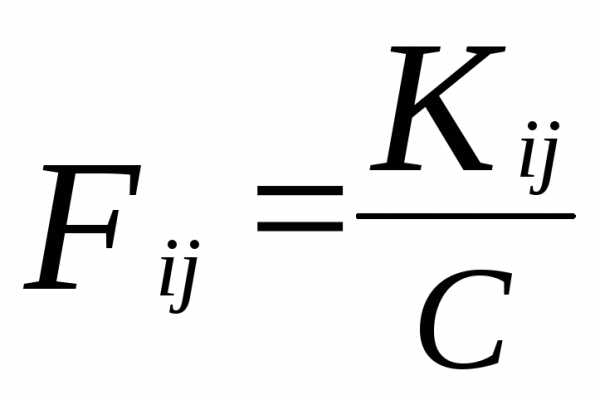где K_ij– число предпочтенийi-м экспертомj-го объекта экспертизы;С– общее число суждений одного эксперта, связанное с числом объектов экспертизыmсоотношением:

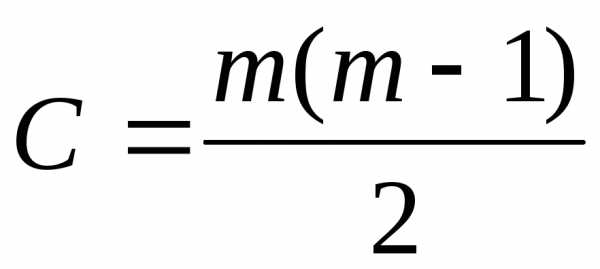
Способ двойного попарного сопоставления. При двойном попарном сопоставлении экспертом заполняется вся таблица, в которой по вертикали и горизонтали проставлены номера объектов экспертизы (показателей качества). В этом случае число суждений экспертов определяется по формуле:

.

Порядок выполнения работы

1. Выбрать самостоятельно объект экспертизы.

2. Определить, к какой группе и подгруппе относится объект, в зависимости от вида промышленной продукции, выбрать основные показатели качества, используя Приложение 21.

3. Выделить наиболее важные показатели, влияющие на качество продукции в целом (6-8 показателей), определить весовые коэффициенты способом ранжирования, результаты расчетов представить в таблице 3.

Таблица 3 – Определение весовых коэффициентов способом ранжирования

эксперты	1	2	3	4	5
показатели качества
1
2
3
4
5
6
7
8

4. Определить весовые показатели способом попарного сопоставления. Составить экспертную группу из 4-х человек. Для каждого эксперта заполнить таблицу 4 (сколько экспертов, столько и таблиц). Рассчитать коэффициенты K_ij,С,F_ij, g_j.

Таблица 4 – Мнение эксперта №

№ объекта экспертизы	1	2	3	4	5	6	7	8
1
2
3
4
5
6
7
8

studfiles.net

Весовые коэффициенты — Энциклопедия по экономике

Когнитивная и мотивационная компоненты оценки продукта потребителями. Шкалы оценки свойств и их оцифровка. Два подхода к комплексной оценке потребительских свойств. Дифференцированная оценка. Модель Розенберга и модель с идеальной точкой. Два варианта модели Розенберга. Сравнительная характеристика, позиционирование и конкурентоспособность товара. Аналитические модели для сравнительной характеристики. Проблемы выбора признаков, шкал и весовых коэффициентов. Задача снижения размерности.  [c.326]
На наш взгляд, было бы целесообразно конституировать особый вид собственности на природные ресурсы, который не подрывал бы территориального единства России, но придавал большой вес (весовой коэффициент) субъектам, субъектам субъектов федерации и т. д. Каждый на закрепленном законом основании должен чувствовать себя тем  [c.108]

Рассуждая в обратном направлении, из такого распределения платежей за недра логично сделать вывод о сущности признаваемой в настоящее время собственности на недра с весовым коэффициентом Уф недра принадлежат всем гражданам России, с коэффициентом Wp — гражданам только данной республики, с WM — жителям района, где расположен этот участок недр. Вообще говоря, такая трактовка не лишена здравого смысла чем ближе живешь, тем больше от этого природного объекта зависишь, тем больше заботишься о нем, тем большими правами по отношению к этому объекту обладаешь.  [c.110]

Затем члены экспертной группы дали свои оценки относительной значимости каждой из пяти рассматривавшихся групп показателей. Эти оценки также были усреднены в целом по всей группе экспертов в виде весовых коэффициентов сравнительной значимости показателей каждой данной группы o j. И наконец, был рассчитан итоговый интегральный критерий эффективности проекта в целом  [c.143]

Группы показателей Усредненная оценка 6j в баллах Весовой коэффициент сравнительной значимости группы показателей tj J6J  [c.146]

Таблица 11 Весовой коэффициент признака р (экспертная оценка)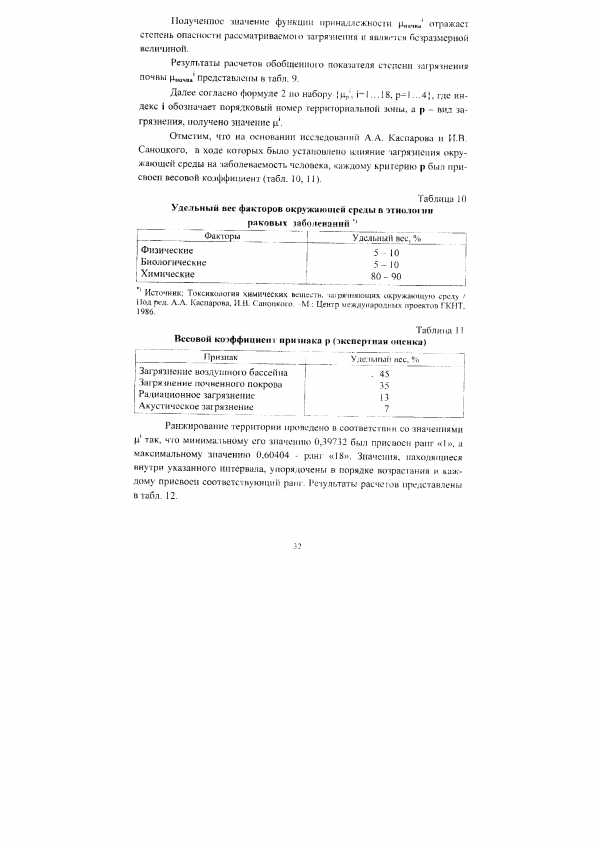

При этом весовые коэффициенты учитывают значимость отдельных групп средств и обязательств с точки зрения сроков поступления средств и погашения обязательств.  [c.54]

Весовые коэффициенты могут быть установлены эмпирически или экспертным методом.  [c.54]

В Методике финансового анализа [ 2 ] эмпирически выведены границы применения весовых коэффициентов и условно приняты  [c.54]

K1,k2,…kn — весовые коэффициенты показателей, определяемые экспертным путем.  [c.65]

Обобщающий показатель финансовой устойчивости предприятия (Z) вычисляется как сумма указанных отношений, взятых с различными весовыми коэффициентами [2]  [c.69]

По мере накопления информации о банкротстве предприятий появится возможность с учетом отраслевых особенностей вносить коррективы в значения весовых коэффициентов и нормативные значения отдельных  [c.69]

Как было показано во второй главе данной работы, в обобщающий (интегральный) показатель финансовой устойчивости предприятия рентабельность производственных фондов входит с наибольшим весовым коэффициентом, т.е. во многом определяет финансовое положение предприятия. Это и обусловливает необходимость тщательного анализа эффективности использования производственных фондов и прежде всего основного капитала (средств труда).  [c.84]

Для указанной оценки может быть (с учетом местных условий) использована методика, широко применяемая в странах с развитой рыночной экономикой, в частности, в США. В соответствии с ней в расчет синтетического (обобщающего) показателя финансовой устойчивости предприятия принимается пять основных финансовых отношений, обладающих наибольшими возможностями прогнозирования, с различными весовыми коэффициентами, определяющие степень их влияния на финансовую устойчивость предприятия.  [c.118]

В число членов формулы финансовой устойчивости предприятия Z показатель рентабельности предприятия Ро входит с наибольшим весовым коэффициентом, что предопределяет существенное значение уровня рентабельности производственных фондов в финансовой устойчивости предприятия.  [c.118]

Изменение прибыли (т.е. ее увеличение или уменьшение) под влиянием различных факторов может быть учтено в расчетах величины обобщающего показателя финансовой устойчивости предприятия. Как следует из формулы расчета данного показателя, рост прибыли будет способствовать увеличению отношения балансовой прибыли к общим активам предприятия (Хз). С учетом весового коэффициента данного отношения (3.3) влияние прироста прибыли за счет какого-либо фактора на изменение величины обобщающего показателя финансовой устойчивости предприятия определится расчетом по формуле  [c.129]

В табл. б также представлены весовые коэффициенты исполь-  [c.62]

Общепризнанный условный прием заключается в объявлении учетной единицей свободного дохода в руках правительства. Тогда можно показать, что соответствующая ставка дисконтирования может быть приблизительно получена из средневзвешенной социальной ставки предпочтения во времени и альтернативной стоимости капитала, используя в качестве весовых коэффициентов те части поступлений от государственного проекта, которые, в среднем, реинвестируются.  [c.99]

Чтобы оценивать затраты и выгоды различно в зависимости. от доходов затронутых проектом лиц, в АЗВ используют «весовые коэффициенты доходов или потребления», основанные, на относительном уровне дохода или потребления затронутого лица. Эти весовые коэффициенты рассчитываются исходя из предполагаемой «предельной полезности дохода или потребления». Эта «предельная полезность определяет, как быстро убывает ценность дополнительной единицы дохода (потребления) по мере возрастания дохода (потребления). Чем выше скорость этого убывания, тем меньший весовой коэффициент присваивается получениям и расходам лиц из групп с высоким доходом.  [c.104]

Весовые коэффициенты определяются по формуле  [c.104]

Весовые коэффициенты определяются по формуле/79/  [c.97]

На четвертом этапе оцениваются предложенные критерии, группируются и отсеиваются те из них, которые не нашли поддержки у большей части экспертов. В основу методологии выявления значимых факторов был положен анализ Парето. Диаграмма Парето (рис.2.3) предназначена для определения вклада различных факторов, влияющих на достижение конечной цели инновационного проекта, и для вычисления весовых коэффициентов. При анализе используются принципы кумулятивного накопления данных и принцип отсекания, основанный на том, что 20% причин обуславливают 80% воздействия. Для организации Парето-анализа коллективу экспертов необходимо провести голосование.  [c.11]

Групповой показатель (G) объединяет единичные показатели (g.) по однородной группе параметров (технических, экономических, эстетических) с помощью весовых коэффициентов (я.), определенных экспертным путем  [c.109]

Этап 3. Все элементы матрицы координат возводятся в квадрат. Если задача решается с учетом разного веса показателей, то полученные квадраты умножаются на величину соответствующих весовых коэффициентов (К), установленных экспертным путем, после чего результаты складываются по строкам (табл. 13. 30)  [c.319]

Каждому из загрязняющих веществ присваивается весовой коэффициент р в зависимости от принадлежности к тому или иному классу опасности веществоДугносящиеся к наиболее опасному классу, имеет максимальную весовую долю в общем объеме загрязнения по каждому рассматриваемому признаку. В табл. 1 показан механизм определения весовых коэффициентов загрязняющих атмосферу и почву веществ.  [c.6]

Структуризация каждого из критериев Рр проводится в соответствии с его значимостью каждому критерию присваивается весовой коэффициент ар в зависимости от степени влияния на здоровье человека на основании исследований Каспарова А.А. и Саноцкого И.В.  [c.8]

В зависимости от принадлежности к тому или иному классу опасности каждому из загрязняющих веществ был присвоен весовой коэффициент. По набору значений цвозд 1=1.. .18, ]-1…4 , согласно формуле 1, был получен обобщенный показатель загрязненности воздушной среды Н-вочд по каждой территориальной зоне (табл. 8).  [c.29]

Отметим, что на основании исследований А.А. Каспарова и И.В. Саноцкого, в ходе которых было установлено влияние загрязнения окружающей среды на заболеваемость человека, каждому критерию р был присвоен весовой коэффициент (табл. 10, 11).  [c.32]

В тех случаях, когда погрешности СО, входящих в комплект, не оданаковы, то соответствующим измерениям приписьшают различный вес Р,, который обратно пропорционален квадрату характеристики погрешности ЛА,. С этой целью для каждого из т СО вычисляют весовой коэффициент  [c.47]

Для упрощения вычислений оценок существует программа GRAFUL , позволяющая строить на экране комплексную графическую модель, вводить связи и весовые коэффициенты. Авторские права на разработку программы принадлежат Центру наукоемкого инжиниринга Санкт-Петербургского государственного политехнического университета. Получаемая в результате вычислений оценка, например 0,7, означает, что в сравнении с идеальным проектом, принятым за 1, данный объект заслуживает внимания. Если полученная оценка составит, к примеру 0,2, это означает, что нет необходимости в затратах времени и средств на данный проект, по крайней мере, без дополнительного осмысления возможных последствий.  [c.64]

economy-ru.info

7.4. Метод распределения весовых коэффициентов

Гражданский кодекс Российской Федерации. Ч. 1. – М: — Омега-Л, 2005.

Федеральный стандарт оценки №1 «Общие понятия оценки, подходы к оценке и требования к проведению оценки (ФСО N I)», утвержден приказом Минэкономразвития Рос­сии от 20 июля 2007 года N 256.

15. Федеральный стандарт оценки №2 «Цель оценки и виды стоимости (ФСО N 2)», утвержден приказом Минэкономразвития России от 20 июля 2007 года N 255.

16. Федеральный стандарт оценки №3 «Требования к отчету об оценке (ФСО N 3)», утвержден приказом Минэкономразвития России от 20 июля 2007 года N 254.

Федеральный стандарт оценки №4 «Определение кадастровой стоимости объек­тов недвижимости (ФСО № 4), утвержден приказом Минэкономразвития России N 508 от 22.10.2010 Европейские стандарты оценки 2009;

Федеральный стандарт оценки № 5 «Виды экспертизы, порядок ее проведения, требования к экспертному заключению и порядку его утверждения (ФСО № 5)», утвержден приказом Минэкономразвития России от «4» июля 2011 г. № 328;

Федеральный стандарт оценки № 6 «Требования к уровню знаний эксперта саморегулируемой организации оценщиков (ФСО № 6)» )», утвержден приказом Минэкономразвития России № 628 от 07.11.2011 г.;

Методические рекомендации по определению рыночной стоимости земельных участков. Утверждено распоряжением Минимущества России от 06.03.2002 № 568-Р. С. 3.

Федеральный закон РФ «О государственной регистрации прав на недвижимое имущество и сделок с ним» от 02.07. 98 года № 125-ФЗ

Закон РФ «Об оценочной деятельности в Российской Федерации» от 29.07.98г. №135-ФЗ

Асаул, А.Н. Экономика недвижимости / А.Н. Асаул. – СПб.: Питер, 2007. – 624 с.

Горемыкин, В.А. Экономика недвижимости. 4-е изд. / В.А. Горемыкин. – М.: Высшее образование, 2007. – 656 с.

Иванова Е.Н. Оценка стоимости недвижимости: учебное пособие / под ред. проф. М.А. Федотовой. – М: КНОРУС, 2007. – 344 с.

Озеров, Е. С. Экономика и менеджмент недвижимости. – СПб.: Издательство «МКС», 2003 — 422 с.

Оценка недвижимости: тесты, задачи, практические ситуации: учебное пособие / под ред. И.В. Грановой. – СПб: Питер, 2002. – 254 с.

Оценка рыночной стоимости недвижимости: учебное пособие / под ред. В.М. Рутгайзера. – М.: Дело, 2007. – 448 с.

Оценка недвижимости: учебник / под ред. проф. А.Г. Грязновой, проф. М.А. Федотовой. – М: Финансы и статистика, 2004. – 496 с

Смагин, В.Н. Экономика недвижимости: учебное пособие / под ред. В.Н. Смагина, В.А. Киселевой. – 2-е пзд., перераб. и доп. – М.: Эксмо, 2008. – 240 с.

Теория и практика оценки для целей девелопмента и управления недвижимостью / С.П. Коростелев. – М.: Маросейка, 2009. – 416 с.

Тесты и задачи по оценочной деятельности: учебное пособие / под ред. В.Е.Есипова, Г.А. Маховиковой, В.В.Тереховой. – СПб: Питер, 2002. – 128 с.

Тэпман, Л.Н. Оценка недвижимости: учебное пособие для вузов / под ред. проф. В.А. Швандара. – М.: ЮНИТИ-ДАНА , 2004. – 303 с.

studfiles.net