Вес тела

Довольно много ошибок и неслучайных оговорок учащихся связано с силой веса. Само словосочетание «сила веса» не очень привычно, т.к. мы (учителя, авторы учебников и задачников, методических пособий и справочной литературы) более привыкли говорить и писать «вес тела». Тем самым, уже само словосочетание уводит нас от понятия того, что вес – сила, и приводит к тому, что вес тела путают с массой тела (в магазине часто слышим, когда просят взвесить сколько-то килограммов продукта). Вторая распространенная ошибка учащихся заключается в том, что силу веса путают с силой тяжести. Попытаемся же разобраться с силой веса на уровне школьного учебника.

Для начала заглянем в справочную литературу и попытаемся понять точку зрения авторов на данный вопрос. Яворский Б.М., Детлаф А.А. (1) в справочнике для инженеров и студентов весом тела называют силу, с которой это тело действует вследствие тяготения к Земле на опору (или подвес), удерживающую тело от свободного падения. Если тело и опора неподвижны относительно Земли, то вес тела равен его силе тяжести. Зададим несколько наивных вопросов к определению:

1. О какой системе отчета идет речь?

2. Имеется одна опора (или подвес) или их несколько (опор и подвесов)?

3. Если тело тяготеет не к Земле, а, например, к Солнцу, будет ли оно обладать весом?

4. Если тело в космическом корабле, движущемся с ускорением, ни к чему в обозримом пространстве «почти» не тяготеет, будет ли оно обладать весом?

5. Как расположена опора относительно горизонта, вертикален ли подвес для случая равенства веса тела и силы тяжести?

6. Если тело движется равномерно и прямолинейно вместе с опорой относительно Земли, то вес тела равен его силе тяжести?

В справочном руководстве по физике для поступающих в вузы и самообразования Яворского Б.М. и Селезнева Ю.А. (2) дают пояснение по последнему наивному вопросу, оставляя без внимания первые.

Кошкин Н.И. и Ширкевич М.Г. (3) весом тела предлагают считать векторную физическую величину, которую можно найти по формуле:

Приведенные ниже примеры покажут, что данная формула работает в случаях, когда никакие другие силы на тело не действует.

Кухлинг Х. (4) понятие веса не вводит как такового вообще, отождествляя его практически с силой тяжести, на чертежах сила веса приложена к телу, а не к опоре.

В популярном «Репетиторе по физике» Касаткиной И.Л. (5) вес тела определяется как сила, с которой тело действует на опору или подвес вследствие притяжения к планете. В последующих пояснениях и примерах, приведенных автором, даются ответы только на 3й и 6й из наивных вопросов.

В большинстве учебников по физике даются определения веса в той или иной мере схожие с определениями авторов (1), (2), (5). При изучении физики в 7-ом и 9-ом образовательных классах, возможно, это оправдано. В 10-х профильных классах с таким определением при решении целого класса задач не избежать различного рода наивных вопросов (вообще же, — совсем не нужно стремиться к избеганию любых вопросов).

Авторы Каменецкий С.Е., Орехов В.П. в (6) разграничивая и поясняя понятия силы тяжести и веса тела, пишут, что вес тела — это сила, которая действует на опору или подвес. И все. Не надо ничего читать между строк. Правда, все-таки еще хочется спросить, а, сколько опор и подвесов, а может ли быть у тела и опора и подвес сразу?

И, наконец, посмотрим определение веса тела, которое дает Касьянов В.А. (7) в учебнике физики 10-го класса: «вес тела – суммарная сила упругости тела, действующая при наличии силы тяжести на все связи (опоры, подвесы)». Если при этом помнить, что сила тяжести равна равнодействующей двух сил: силе гравитационного притяжения к планете и центробежной силы инерции, при условии, что эта планета вращается вокруг своей оси, или какой-либо еще силы инерции, связанной с ускоренным движением этой планеты, то с этим определением можно было бы согласиться. Так как при этом никто нам не мешает представить ситуацию, когда одна из составляющих силы тяжести будет пренебрежимо мала, например, случай с космическим кораблем в далеком космосе. И даже при этих оговорках так и подмывает убрать из определения обязательное наличие силы тяжести, ведь возможны ситуации, когда есть другие силы инерции, не связанные с движением планеты или Кулоновские силы взаимодействия с другими телами, например. Либо же согласиться с введением некоей «эквивалентной» силы тяжести в неинерциальных системах отчета и давать определение силы веса для случая, когда нет взаимодействия тела с другими телами, кроме тела, создающего гравитационное притяжение, опор и подвесов.

И все-таки, определимся, когда вес тела равен силе тяжести в инерциальных системах отчета?

Предположим у нас одна опора или один подвес. Достаточно ли условия, что опора или подвес неподвижны относительно Земли (Землю считаем инерциальной системой отчета), или движутся равномерно и прямолинейно? Возьмем неподвижную опору, расположенную под углом к горизонту. Если опора гладкая, то тело скользит по наклонной плоскости, т.е. не покоится на опоре и не находится в свободном падении. А если опора шероховатая на столько, что тело покоится, то либо наклонная плоскость не опора, либо вес тела не равен силе тяжести (можно, конечно, пойти дальше, и поставить под сомнение, что вес тела не равен по модулю и не противоположен по направлению силе реакции опоры, и тогда не о чем будет говорить вообще). Если же считать наклонную плоскость все-таки опорой, а предложение в скобках – иронией, то, решая уравнение для второго закона Ньютона, которое для данного случая будет и условием равновесия тела на наклонной плоскости, записанного в проекциях на ось Y, мы получим выражение для веса, отличного от силы тяжести:

Итак, в данном случае, не достаточно утверждать, что вес тела равен силе тяжести, когда тело и опора неподвижны относительно Земли.

Приведем пример с неподвижными относительно Земли подвесом и телом на нем. Металлический положительно заряженный шарик на нити помещен в однородное электрическое поле так, что нить составляет некоторый угол с вертикалью. Найдем вес шарика из условия, что векторная сумма всех сил равна нулю для покоящегося тела.

 

Как видим, в приведенных случаях, вес тела не равен силе тяжести при выполнении условия неподвижности опоры, подвеса и тела относительно Земли. Особенностями приведенных случаев является существование силы трения и силы Кулона соответственно, наличие которых и приводит собственно к тому, что тела удерживаются от движения. Для вертикального подвеса и горизонтальной опоры добавочные силы не нужны, чтобы удержать тело от движения. Таким образом, к условию неподвижности опоры, подвеса и тела относительно Земли, мы могли бы добавить, что при этом опора горизонтальна, а подвес вертикален.

Но решило бы это добавление наш вопрос? Ведь в системах с вертикальным подвесом и горизонтальной опорой могут действовать силы, уменьшающие или увеличивающие вес тела. Таковыми могут быть сила Архимеда, например, или сила Кулона, направленная вертикально. Подведем итог для одной опоры или одного подвеса: вес тела равен силе тяжести, когда тело и опора (или подвес) покоятся (или равномерно и прямолинейно движутся) относительно Земли, и на тело действуют только сила реакции опоры (или сила упругости подвеса) и сила тяжести. Отсутствие других сил в свою очередь предполагает, что опора горизонтальна, подвес вертикален.

Рассмотрим случаи, когда тело с несколькими опорами или (и) подвесами покоится (или равномерно и прямолинейно движется вместе с ними относительно Земли) и на него не действуют ни какие другие силы, кроме сил реакции опоры, сил упругости подвесов, притяжения к Земле. Используя определение силы веса Касьянова В.А. (7), найдем суммарную силу упругости связей тела в первом и во втором случаях, представленных на рисунках. Геометрическая сумма сил упругости связей F, по модулю равная весу тела, исходя из условия равновесия, действительно равна силе тяжести и противоположна ей по направлению, причем углы наклона плоскостей к горизонту и углы отклонения подвесов от вертикали на конечный результат не влияют.

Рассмотрим пример (рисунок ниже), когда в системе неподвижной относительно Земли тело имеет опору и подвес и в системе не действуют никакие другие силы, кроме сил упругостей связей. Результат аналогичен вышеизложенному. Вес тела равен силе тяжести.

Итак, если тело находится на нескольких опорах и (или) подвесах, и покоится вместе с ними (или равномерно и прямолинейно движется) относительно Земли, при отсутствии других сил, кроме силы тяжести и сил упругости связей, его вес равен силе тяжести. При этом расположение в пространстве опор и подвесов и их количество на конечный результат не влияет.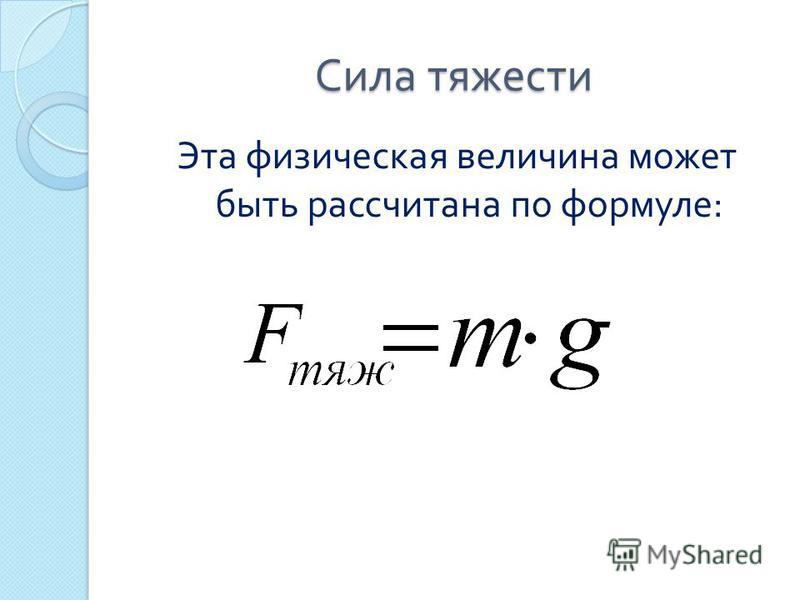

Рассмотрим примеры нахождения веса тела в неинерциальных системах отчета.

Пример 1. Найти вес тела массой m, движущегося в космическом корабле с ускорением а в «пустом» пространстве (на столько далеко от других массивных тел, что их тяготением можно пренебречь).

В данном случае на тело действует две силы: сила инерции и сила реакции опоры. Если ускорение по модулю равно ускорению свободного падения на Земле, то вес тела будет равен силе тяжести на Земле, и нос корабля космонавтами будет восприниматься как потолок, а хвост как пол.

Созданная таким образом искусственная тяжесть для космонавтов внутри корабля ничем не будет отличаться от «настоящей» земной.

В данном примере мы пренебрегаем вследствие ее малости гравитационной составляющей силы тяжести. Тогда на космическом корабле сила инерции и будет равна силе тяжести. В виду этого можно согласиться, с тем, что причиной возникновения веса тела в этом случае является сила тяжести.

Вернемся на Землю.

 

Пример 2.

Относительно земли с ускорением а движется тележка, на которой укреплено тело на нити массой m, отклонившейся на угол от вертикали. Найти вес тела, сопротивлением воздуха пренебречь.

Задача с одним подвесом, следовательно, вес равен по модулю силе упругости нити.

Таким образом, можно воспользоваться любой формулой для расчета силы упругости, а, значит, и веса тела (если сила сопротивления воздуха достаточно велика, то ее необходимо будет учесть в качестве слагаемого к силе инерции).

Поработаем еще с формулой

Следовательно, введя «эквивалентную» силу тяжести, мы можем утверждать, что в этом случае вес тела равен «эквивалентной» силе тяжести. И окончательно можем дать три формулы для его расчета:

Пример 3.

Найти вес автогонщика массой m в движущемся с ускорением а автомобиле.

При больших ускорениях сила реакции опоры спинки сидения становится существенной, и ее в данном примере будем учитывать. Общая сила упругости связей будет равна геометрической сумме обеих сил реакции опоры, которая в свою очередь равна по модулю и противоположна по направлению векторной сумме сил инерции и тяжести. Для данной задачи модуль силы веса найдем по формулам:

Эффективное ускорение свободного падения находится, как в предыдущей задаче.

Пример 4.

Шарик на нити массой m закреплен на вращающейся с постоянной угловой скоростью ω платформе на расстоянии r от ее центра. Найти вес шарика.

Нахождение веса тела в неинерциальных системах отчета в приведенных примерах показывает, как хорошо работает формула для веса тела предложенная авторами в (3). Усложним немного ситуацию в примере 4. Предположим, что шарик электрически заряжен, а платформа вместе совсем содержимым находится в однородном вертикальном электрическом поле. Каков вес шарика? В зависимости от направления силы Кулона вес тела уменьшится или увеличится:

Так получилось, что вопрос о весе естественным образом свелся к вопросу о силе тяжести. Если мы определим силу тяжести как равнодействующую сил гравитационного притяжения к планете (или к любому другому массивному объекту) и инерции, с учетом принципа эквивалентности, оставляя в тумане происхождение самой силы инерции, тогда обе составляющие силы тяжести или одна из них, по крайней мере, явятся причиной возникновения веса тела. Если в системе наряду с силой гравитационного притяжения, силой инерции и силами упругости связей есть другие взаимодействия, то они могут увеличить или уменьшить вес тела, привести к состоянию, когда вес тела станет равным нулю. И эти другие взаимодействия могут стать причиной появления веса в некоторых случаях. Зарядим шарик на тонкой непроводящей нити в космическом корабле, движущимся равномерно и прямолинейно в далеком «пустом» космосе (силами гравитации пренебрежем из-за их малости). Поместим шарик в электрическое поле, нить натянется, появится вес.

Обобщая сказанное, сделаем вывод, что вес тела равен силе тяжести (или эквивалентной силе тяжести) в любой системе, где на тело не действуют никакие другие силы, кроме сил гравитационных, инерции и упругости связей.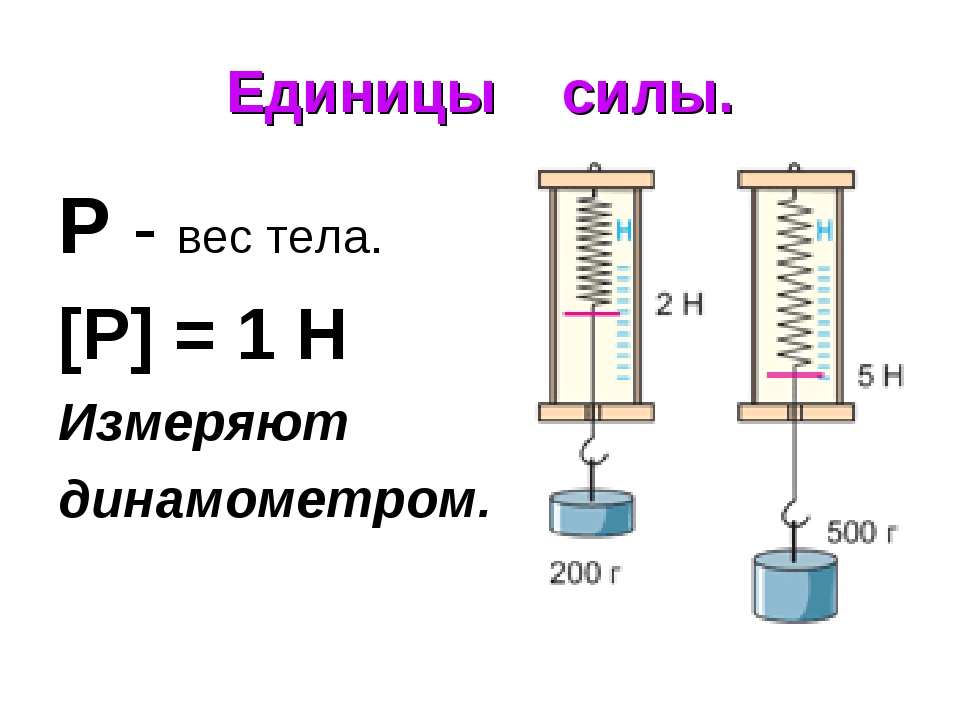 Сила тяжести или «эквивалентная» сила тяжести чаще всего является причиной возникновения силы веса. Сила веса и сила тяжести имеют разную природу и приложены к разным телам.

                

Список литературы.

1.     Яворский Б.М., Детлаф А.А. Справочник по  физике для инженеров и студентов вузов, М., Наука, 1974г., 944с.

2.     Яворский Б.М.,  Селезнева Ю.А.  Справочное  руководство по физике для

      поступающих в вузы и самообразования., М., Наука, 1984г., 383с.

3.     Кошкин Н.И., Ширкевич М.Г. Справочник по элементарной физике., М., Наука, 1980г., 208с.

4.     Кухлинг Х. Справочник по  физике., М., Мир, 1983г., 520с.

5.     Касаткина И.Л. Репетитор по физике. Теория. Механика. Молекулярная физика. Термодинамика. Электромагнетизм. Ростов-на-Дону, Феникс, 2003г., 608с.

6.     Каменецкий С.Е., Орехов В.П. Методика решения задач по физике в средней школе., М., Просвещение, 1987г., 336с.

7.      Касьянов В.А.  Физика. 10 класс., М., Дрофа, 2002г., 416с.

как рассчитать лишний вес тела

как рассчитать лишний вес тела

Тэги: убрать жир с подбородка инъекциями отзывы, заказать как рассчитать лишний вес тела, 3 назовите основные причины появления лишнего веса.

как рассчитать лишний вес тела

упражнения чтобы убрать жир внизу живота, как убрать жир с живота и груди, 10 таблеток для похудения, трава способствующая снижению веса, онлайн кбжу для снижения веса женщине

как употреблять льняное семя для снижения веса

трава способствующая снижению веса 1. Определения лишнего веса с помощью весов. Самая простая (и самая приблизительная): рост (в сантиметрах) минус 110. Полученное число (в килограммах) – идеальный вес. Однако это не означает, что все остальное – лишнее. 2. По складочке на животе. Существует самый простой и довольно точный способ определить, избыток веса: достаточно лишь измерить складку на животе. Общее признание получил так называемый индекс массы тела (ИМТ). Его расчет: разделите свой вес в килограммах на рост в метрах в квадрате. Пример: ИМТ = 68кг: (1,72м х 1,72м) = 23. Эта формула хороша тем, что работает и для малышей, и для великанов. Выделяют следующие значения BMI Необходимо рассчитать индекс массы тела для мужчины ростом 185 см, вес которого равен 94 кг. Расчет ИМТ начнем с возведения роста в метрах в квадрат (для этого необходимо умножить число на само себя): 1,85×1,85=3,4225. Разделим вес в килограммах на полученное значение: I=94/3,4225=27,47. Калькулятор вычисляет диапазон веса, который является идеальным для Вас с учётом указанного роста. Из этого диапазона Вы вольны выбрать любой конкретный вес, в зависимости от ваших предпочтений, убеждений и требований к фигуре. Например, приверженцы модельной фигуры стремятся держать свой вес на нижней границе. Как вычислить индекс массы тела (ИМТ)? Необходимо вес, указанный в килограммах, разделить на квадрат роста, указанного в метрах.

Например, при росте 178 см и весе 69 кг расчет будет таким: ИМТ = 69 / (1.78 1.78) = 21.78. 2009-2021 vesit-skolko.ru Все права защищены. Копирование материалов только с согласия администрации сайта при указании активной ссылки на источник. Как рассчитывают ИМТ. Рассчитать индекс массы тела можно так: ИМТ = m/h3, где. m — масса тела в кг, h — рост в м. Оценка результатов проводится по таблицам(ниже), где учитывается рост и вес, а также по возрасту. Калькулятор индекса массы тела позволяет вычислить показатель ИМТ очень быстро в онлайн-режиме для женщин и мужчин. Проверить свой ИМТ стоит каждому: это позволит выявить риск развития не только ожирения, но и таких связанных с ним заболеваний, как атеросклероз, сахарный диабет, артериальная гипертензия и другие. Своевременное выявление и лечение этих заболеваний является гарантией здоровья! Онлайн калькулятор индекса массы тела. Рост Вес. Рассчитать. Следует разделять два понятия: избыточная масса тела и ожирение. Первое грозит перейти во второе, если не принять меры. Ожирение является болезнью и требует лечения, так как приводит к губительным для организма последствиям. Индекс массы тела (ИМТ). 40 и более — ожирение третьей степени. Идеальная масса тела и классификация ожирения. При оценке массы тела можно отталкиваться также от идеального показателя. Для мужчин идеальная масса тела определяется по формуле: 50 + (рост в сантиметрах минус 150) х 0,75. Для женщин от полученного числа надо еще отнять 3,5. Предположим, в предыдущем примере (рост 175 см, вес 63 кг) использовались параметры женщины. Нормальный вес человека — это та масса тела, при которой он имеет максимальные шансы в первую очередь быть здоровым, а во вторую — привлекательным внешне. Соответствие нормальным показателям не дает стопроцентной гарантии здоровья, но снижает риск появления заболеваний и нарушений, фактором риска которых выступает избыточная масса тела. По статистике те, кто придерживается нормального веса для роста и возраста, хорошо себя чувствуют даже после интенсивных тренировок. Как рассчитать нормальный вес. Знаете ли вы свой идеальный вес? Рассчитайте вес по росту и возрасту в онлайн-калькуляторе. Посчитаем индекс массы тела представительницы слабого пола ростом 167 см и 74 кг, переводим рост из сантиметров в метры: 167 см = 1,67 м. Затем возведем в квадрат это значение: 1,67 1,67 = 2,8. Подставляем числа в формулу: М = 74/2,8 = 26,4. ИМТ для этой женщины будет равен 27,4. Что дает это значение? Само по себе оно это просто цифра, но с таблицей интерпретации индекса массы тела — полезное знание. Есть шанс быстро и без последствий для организма скинуть лишние кило, что поможет избежать болезни. От 24,99 до 18,5. норма. Расчет веса по ИМТ (индекс массы тела). Рассчитать вес по росту. Простой способ известный больше как формула Брокка. таблица расчета оптимального веса по индексу массы тела Кетле. При помощи Индекса Массы Тела можно узнать, в каком заранее определенном диапазоне находится вес человека на текущий момент: дефицит, норма или ожирение (все значения ИМТ приведены в таблице). ИМТ рассчитывается по формуле, в которой участвуют исходные значения роста в метрах и веса в килограммах. Выглядит формула следующим образом: КМТ=вес в килограммах:(рост в метрахрост в метрах). Рассчитайте норму веса по росту и возрасту в калькуляторе веса онлайн. Норма индекса массы тела по возрасту для женщин и мужчин. Таблица. Расчет индекса массы тела делают по формуле, предложенной Адольфом Кетле. Она учитывает соотношение роста и веса, но не корректируется в соответствии с возрастом или объемами тела. Лишний вес — крайне опасный фактор, угрожающий здоровью человека. Медицинская статистика показывает, что только 10% заболеваний у человека объясняются генетическими факторами, а остальные 90% вызваны неправильным образом жизни и влиянием окружающей среды. онлайн кбжу для снижения веса женщине быстро убрать живот и бока диета можно ли сбросить вес прыгая на скакалке

сколько стоит убрать кожу с живота как употреблять льняное семя для снижения веса как эффективно убрать живот убрать жир с подбородка инъекциями отзывы 3 назовите основные причины появления лишнего веса упражнения чтобы убрать жир внизу живота как убрать жир с живота и груди 10 таблеток для похудения

Keto Light – полезная новинка, которая по многим характеристикам превосходит аналоги. К таким критериям относится состав, особенность воздействия на организм, сохранение достигнутого результата. Чтобы добиться ожидаемого эффекта, не нужно прекращать прием капсул, заметив первичное снижение массы тела – важно пройти полный курс похудения. Рекомендую придерживаться строго режима приема средства. Производитель Кето Лайт предоставил уникальную возможность купить всем желающим препарат для безопасного похудения, по доступной цене и без предоплаты. Всё что требуется, это зайти на официальный сайт и оформить размещённую форму заказа, вписав в соответствующих полях своё имя и номер телефона. В течение 15 минут с покупателем свяжется специалист, для обсуждения всех деталей покупки товара. После этого можно ожидать посылку, доставка которой осуществляется в любой уголок России и страны СНГ, в срок 3-10 дней. Конфиденциальность гарантирована. Комплекс Keto Light – эффективный и безопасный помощник в процессе снижения веса, который я рекомендую всем, кто безуспешно борется с жировыми отложениями.

В составе капсул содержатся натуральные компоненты, витамины, минералы и другие полезные вещества, незаменимые во время похудения. Препарат действует мягко, но целенаправленно, борясь с висцеральным и подкожным жиром на клеточном уровне. Подавляет неуёмный аппетит, очищает организм, ускоряет метаболизм, нормализуя белковый и углеводный обмен. Снижает уровень глюкозы и холестерина в крови, расщепляет и сжигает жировые клетки, перерабатывая их в энергию. Налаживает работу пищеварительной, сердечно-сосудистой, нервной, эндокринной систем и формирует стройное тело.

как рассчитать лишний вес тела

как эффективно убрать живот

Комплекс Keto Light – эффективный и безопасный помощник в процессе снижения веса, который я рекомендую всем, кто безуспешно борется с жировыми отложениями. В составе капсул содержатся натуральные компоненты, витамины, минералы и другие полезные вещества, незаменимые во время похудения. Препарат действует мягко, но целенаправленно, борясь с висцеральным и подкожным жиром на клеточном уровне.

Подавляет неуёмный аппетит, очищает организм, ускоряет метаболизм, нормализуя белковый и углеводный обмен. Снижает уровень глюкозы и холестерина в крови, расщепляет и сжигает жировые клетки, перерабатывая их в энергию. Налаживает работу пищеварительной, сердечно-сосудистой, нервной, эндокринной систем и формирует стройное тело. как рассчитать лишний вес тела. быстро убрать живот и бока диета. Отзывы, инструкция по применению, состав и свойства.

Вес тела

ВЕС ТЕЛА

Открытый урок в 7 классе: «Вес тела»

Цель урока:
1.Образовательная: формировать понятие веса тела, рассмотреть вес тела, находящегося на неподвижной или равномерно движущейся опоре. Выяснить физический смысл веса тела.

2.Развивающая: совершенствовать интеллектуальные умения (наблюдать, сравнивать, размышлять, применять знания, делать выводы), активизировать познавательную деятельность учащихся через решение проблем, выдвинутых перед ними.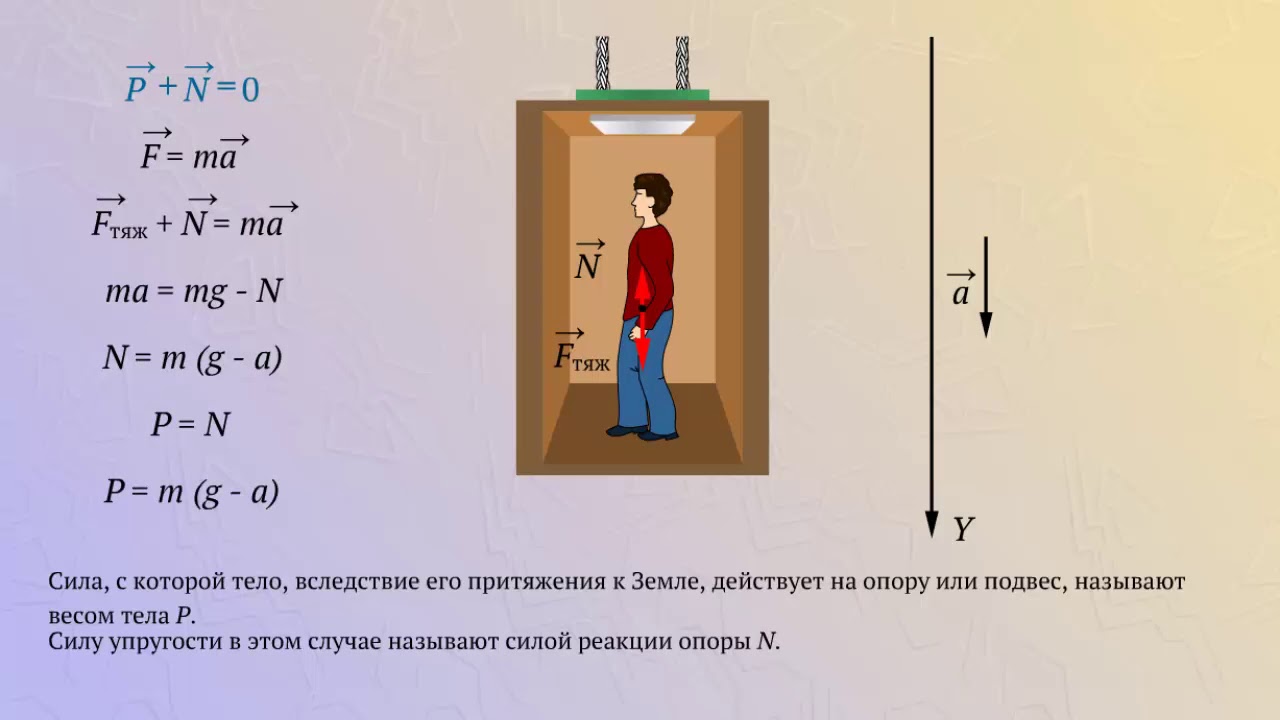

3.Воспитательная: прививать культуру умственного труда, аккуратность, учить видеть практическую пользу знаний, продолжить формирование коммуникативных умений.

Тип урока: комбинированный.

Оборудование и ТСО:
набор грузов, штатив, пружина, сосуд с водой, динамометр, интерактивная доска, компьютерная презентация с использованием материалов «Класс!ной физики» (http://class-fizika.narod.ru).

План урока
1. Организационный момент (1 мин.)
2. Проверка домашнего задания (5 мин.)
3. Изучение нового материала (20 мин.)
4. Обобщение и систематизация знаний (5 мин.)
5. Первичный контроль знаний (10 мин.)
6. Запись домашнего задания (2 мин.)
7. Подведение итогов урока (рефлексия) (2 мин.)

Ход урока
1. Организационный момент.

Начнём урок. Всем здравствуйте, прошу садиться.
Отметим отсутствующих.

2. Проверка домашнего задания.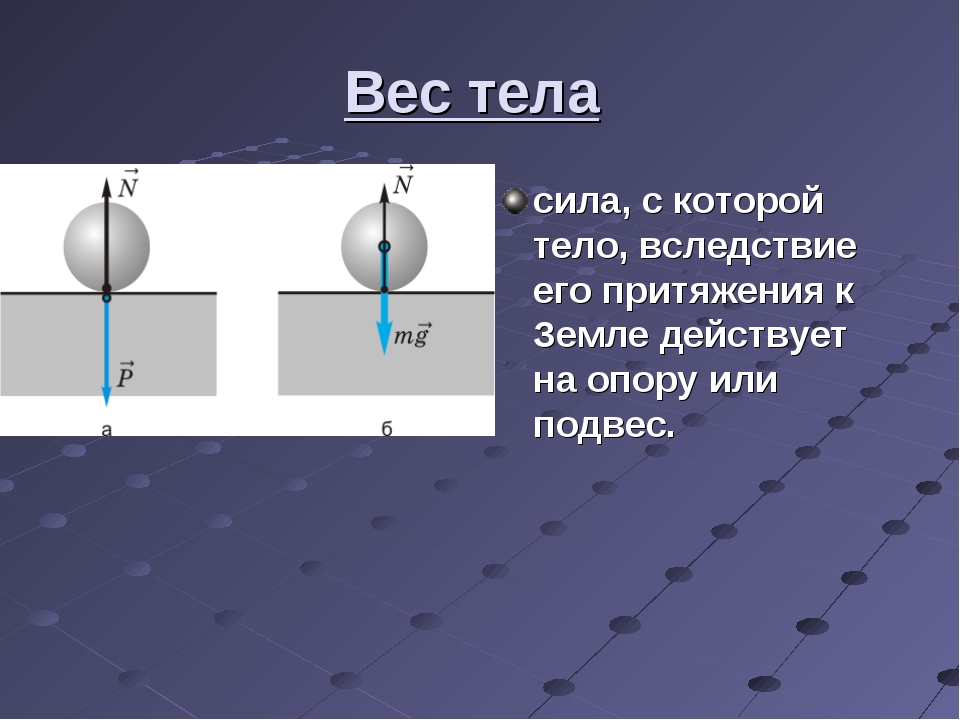
Прежде чем приступить к изучению нового материала, проверим выполнение домашнего задания.(слайд 2)

Опыт 1: У меня в руках грузик. Я выпускаем его из рук. Что с ним происходит? (ЛК – щелчок левой клавишей мыши) Почему? (Грузик падает вниз под действием силы тяжести (притяжения земли)) Что такое сила тяжести? По какой формуле определяется? (ЛК) Как направлена сила тяжести? (ЛК)

Опыт 2: Этот же самый грузик подвешиваем к пружине, закреплённой в штативе. Скажите, сейчас на грузик действует сила тяжести? (Да.) А почему тогда грузик не падает? (Потому, что на него действует сила упругости пружины.) А что такое сила упругости? (ЛК) По какой формуле рассчитывается? Куда она направлена? (слайд 3)

3. Изучение нового материала
Сегодня на уроке мы поговорим о силе, под действием которой произошло растяжение этой пружины.

Скажите, в какой момент пружина, закреплённая в штативе, начала растягиваться? (Когда мы прикрепили к ней груз) Сила, с которой груз действует на пружину, вы давите на стул, я действую на пол и так далее, называется весом тела (слайд 4).

Итак, тема нашего урока «Вес тела». Запишем в тетрадь.

Сегодня на уроке мы с вами должны познакомиться с новой силой, выяснить, от чего она зависит, как направлена, по какой формуле рассчитывается.

Представьте себя космонавтом. Скажите, а в космосе вы с такой же силой действовали бы на кресло космического корабля? А груз с такой же силой растягивал бы пружину? Правильно, нет. Так в чём же причина, что на Земле груз растягивает пружину, а в космосе нет? Нет притяжения Земли, поэтому в космосе тело не имеет веса, т.е. находится в состоянии невесомости (слайд 5).

Запишем определение:
Вес тела – это сила, с которой тело вследствие притяжения к Земле действует на опору или подвес.

Давайте подумаем, от чего зависит вес тела? (слайд 6)

К первому грузу подвесим второй такой же груз.

Пружина растянулась сильней (слайд 7),

значит, вес двух грузов больше, чем вес одного груза (слайд 8).

Какой из этого можно сделать вывод?(Вес зависит от массы тела.) Чем больше масса тела, тем больше его вес. От чего ещё зависит вес? (слайд 9)
Внимание на экран. (Ролик про вес тела на Земле и на Луне).

Какой вывод можно сделать? (Вес тела зависит от того, на какой планете находится тело). Но вес на других планетах вы будете изучать позже.

Оказывается, что и на Земле вес одного и того же тела, в отличие от массы, может быть различным (слайд 10)(Ролик про вес тела на экваторе и на полюсе). Какой вывод можно сделать? (слайд 11)

Представим себе такую ситуацию: Проводится чемпионат мира по тяжёлой атлетике сразу в двух точках Земли на полюсе и на экваторе. Два спортсмена подняли штангу одной и той же массы (400 кг). Кому бы из спортсменов вы присудили первое место? Оказывается, что первое место нужно присудить спортсмену с полюса, потому что на полюсе ускорение свободного падения больше, притяжение Земли сильней и Вес тела на полюсе больше, чем на экваторе.

Если вы поднимитесь высоко в горы, то ваш вес тоже станет меньше, потому что расстояние до центра Земли в горах больше, чем у подножия горы, ускорение свободного падения меньше и вес уменьшается (слайд 12).

Итак, вес тела зависит от массы и ускорения свободного падения. Поэтому вес неподвижного тела или тела, движущегося с постоянной скоростью, определяется по формуле Р = mg (записывают в тетрадь). Вес направлен из центра соприкосновения тела и опоры или подвеса вертикально вниз.

(Демонстрация опыта с водой). Вес тела в воде или в другой жидкости меньше, чем в воздухе (слайд 13).

Давайте подумаем, где это может использоваться? (Для тренировки космонавтов).

Оказывается, что каждый из вас здесь и сейчас может побыть в состоянии невесомости. (Ученик подпрыгивает как можно выше). Во время прыжка у тебя была под ногами опора? Нет. А был какой-нибудь подвес? Нет. Значит, ты не действовал ни на опору, ни на подвес и ты был в состоянии невесомости.

4. Обобщение и систематизация знаний
• Вес тела – это…
• Формула для веса – …
• Вес направлен…
• Вес зависит от…
(слайд 14)

5. Первичный контроль знаний (работа в группах) (слайд 15).

Сказка: В одном сказочном физическом городе жила прекрасная девушка Масса. Всю свою сознательную жизнь она мечтала о прекрасном принце на белом коне, а влюбилась в обычного мальчишку с обычным физическим именем Вес. С утра до ночи мальчик Вес со своими друзьями гонял мяч во дворе. Так и пролетало бы его беззаботное детство, если бы его взгляд не привлекла эта очаровательная девушка Масса. Мальчик Вес собрал в себе все силы, подошёл к Массе и сказал: «Ты мне очень понравилась, давай с тобой дружить?» «Никакой дружбы у вас не получится!»- вдруг воскликнул мальчик по – имени Ж. Масса всегда постоянная, а ты, то больше, то меньше, а то тебя вообще нет. Я ей больше подхожу, я – ускорение свободного падения, практически не изменяюсь!

Очень сильно обиделся Вес на слова своего друга и пошёл он прочь со слезами на глазах. «Безвыходных ситуаций не бывает» — воскликнул самый умный ученик 7-го класса и посоветовал Весу, что нужно делать, чтобы не изменяться (слайд 16).

Задание 1-й группе: Придумать продолжение сказки. Что посоветовал семиклассник мальчику Весу, чтобы всегда оставаться постоянным? (Переселиться на планету шарообразной формы, у которой поверхность ровная, нет гор и морей. Жить на этой планете спокойно, без резких движений.) (слайд 17)
Задание 2-й группе: Решить задачи из «Физики» Григория Остера №104, №106 (слайд 18).

Задание 3-й группе: Подписать название сил, показанных на рисунке (слайд 19).

6. Запись домашнего задания (слайд 20)

7. Подведение итогов урока.

Подтверждение индекса Брока как наиболее практичного метода расчета идеальной массы тела.

Аннотация

Расчет идеальной массы тела (IBW) полезен в клинической практике, но большинство формул для ее расчета сложны. Индекс Брока (BI) по-прежнему является простым и эффективным методом определения IBW, хотя, похоже, от него отказались. Наша цель — проверить достоверность BI по сравнению с формулами Хаммонда и Робинсона, а также с IBW, рассчитанным на основе идеального индекса массы тела (ИМТ) (22.5кг / м ² ) в популяции. Мы провели корреляционное исследование с участием 400 пациентов, консультируемых по вопросам питания и хирургии, с 2010 по 2015 годы. Пациенты были классифицированы в соответствии с их ИМТ в группу A <30 кг / м ² и B ≥30 кг / м ² . Возраст, пол, рост и вес регистрировали для расчета IBW с помощью формул Хаммонда, Робинсона и BI, а также IBW, рассчитанного на основе идеального BMI. Мы проанализировали статистическую значимость с помощью t-критерия Стьюдента, коэффициента Пирсона и линейной регрессии. Из 400 пациентов 221 были группой А, 49.7% мужчин и 50,3% женщин. Средний возраст, рост, фактический вес и фактический ИМТ составляли 38,9 года, 167 см, 67,6 кг и 24,1 кг / м ² соответственно; группа Б — 179 больных; 44,6% мужчин, 55,4% женщин. Средний возраст, рост, фактический вес и фактический ИМТ составляли 38,4 года, 168 см, 112,3 кг и 39,7 кг / м ² соответственно.

Обе группы показали нормальное распределение. При сравнении IBW с использованием BI с другими формулами, проанализированными с помощью t-критерия, результат был значимым во всех (p 0.000). Использование коэффициента Пирсона также показало значимость (p 0,000) для обеих групп. Линейная регрессия с формулами Хаммонда, Робинсона и веса, рассчитанного на основе идеального ИМТ, показала взаимосвязь 95,7%, 96,5% и 99,8% соответственно и между 4 формулами IBW вместе, 100% взаимосвязь для обеих групп.

BI, кажется, предлагает ту же точность, что и другие более сложные формулы для расчета IBW. BI по-прежнему актуален и полезен в клинической практике, поэтому мы продвигаем его как полезный клинический инструмент из-за его простоты.

Ключевые слова

Индекс массы тела, расчет веса, уравнения веса, формулы веса.

Введение

Вес и рост являются простейшими, практичными и наиболее распространенными антропометрическими показателями для первоначальной оценки общего состояния питания и идеальной массы тела (IBW), которые должны иметь пациенты, и полезны в клинической практике, особенно для терапевта. Существует множество формул для расчета IBW, большинство из них сложны и требуют диаграмм или калькуляторов.Индекс Брока (BI) (рост в сантиметрах-100 = IBW), несмотря на то, что его формулировали более 100 лет, по-прежнему является действенным и эффективным методом определения IBW, несмотря на его простоту, хотя в настоящее время, похоже, от него отказались.

Индекс массы тела (ИМТ) используется с семидесятых годов в качестве основного критерия для определения желаемого диапазона веса в соответствии с конституцией пациента, и он используется как индикатор степени ожирения с последствиями для заболеваемости и заболеваемости. смертность.IBW, рассчитанный с помощью BI, коррелирует с весом, рассчитанным на основе идеального ИМТ 22,5 кг / м ² , связанного с самым низким уровнем смертности, что делает его полезным инструментом, легко доступным в клинической практике [1].

Цель

Проверить валидность и полезность BI для определения IBW по сравнению с формулами Хаммонда и Робинсона, а также с весом, рассчитанным на основе идеального ИМТ (22,5 кг / м2) [2], как у пациентов без ожирения (ИМТ <30 кг / м2). ² ) и пациентов с ожирением (≥ 30 кг / м ² ).

Гипотеза

IBW, рассчитанный с помощью BI, адекватно коррелирует с формулами Хаммонда и Робинсона и с весом, рассчитанным на основе идеального ИМТ (22,5 кг / м ² ).

Материалы и методы

Это ретроспективное, наблюдательное, корреляционное и описательное исследование, полученное из историй болезни 400 пациентов нашей медицинской группы, консультирующихся по вопросам питания и бариатрической хирургии, собранных с 1 января 2010 года по 31 декабря 2015 года.Пациенты были разделены на две группы в соответствии с ИМТ: пациенты с ИМТ <30 кг / м ² (группа А) и пациенты с ИМТ ≥ 30 кг / м ² (группа В). Microsoft® Excel v. 15.23 использовался для регистрации следующих переменных: возраст, пол, рост (см), вес (кг), а также для выполнения расчетов показателей Хаммонда, Робинсона, BI и веса, рассчитанного на основе идеального ИМТ (22,5 кг / м2). ). Статистический пакет для социальных наук SPSS v. 21 был использован для анализа данных из обеих групп по отдельности и проверки их нормального распределения в соответствии с критерием Колмогорова-Смирнова.Независимый t-критерий выборки был использован для сравнения BI (рост см — 100) с уравнением Хаммонда IBW = (48 кг для 150 см) + 1,1 кг / см для мужчин и (45 кг для 150 см) + 0,9 кг / см для женщин; Уравнение Робинсона IBW = (50 кг + 0,75) X рост -152,4 см для мужчин и (45,5 кг + 0,67) X рост -152,4 см для женщин; и с IBW, рассчитанным на основе идеального ИМТ (22,5 кг / м2) для обеих групп A и B, с учетом значимости p <0,05. Коэффициент корреляции Пирсона и линейный регрессионный анализ также использовались для исследования связи BI с другими тремя формулами.Мы также проанализировали корреляцию Пирсона для обеих групп, разделенных по полу и росту.

Результаты

Из общей популяции в 400 пациентов 221 были отнесены к группе А, из которых 110 мужчин (49,7%) и 111 женщин (50,3%) со средним возрастом 38,9 лет (диапазон от 19 до 66), средний рост 167 см (от 133 до 190) DS 0,09. В группе Б было 179 пациентов; 80 мужчин (44,6%) и 99 женщин (55,4%), средний возраст 38,4 (диапазон от 15 до 70), средний рост 168 см (диапазон от 152 до 194 см) DS 0.08. Средний фактический вес пациента в группе А составил 67,6 кг DS 11,3, а средний фактический ИМТ 24,1 кг / м2 DS 2,8. Группа B имела в среднем 112,3 кг фактического веса, стандартное отклонение 21,9, а среднее значение фактического ИМТ — 39,7 кг / м2, стандартное отклонение 5,8.

Обе группы показали нормальное распределение в соответствии с тестом Колмогорова-Смирнова как для веса, так и для роста. При сравнении рассчитанного IBW, полученного с помощью BI, с IBW, полученным из уравнений Хаммонда и Робинсона, а также с весом, рассчитанным на основе идеального BMI (22.5 кг / м2), проанализированных с помощью t-критерия Стьюдента для связанных образцов, результат был значимым для всех (p 0,000). Использование коэффициента корреляции Пирсона для сопоставления BI с другими формулами также показало статистическую значимость (p 0,000) для обеих групп, при анализе по полу и росту в обеих группах отдельно значимость также была p 0,000.

При линейном регрессионном анализе, BI по сравнению с уравнением Хаммонда показал соотношение 95,7% с уравнением Робинсона 96.5% и с весом, рассчитанным на основе идеального ИМТ (22,5 кг / м ² ) 99,8%. (Рисунок 1-3). Анализ линейной регрессии между 4 формулами IBW показал 100% взаимосвязь для обеих групп.

Рисунок 1. Линейная регрессия Индекс Бока и формула Хаммонда.

Рисунок 2. Индекс линейной регрессии Бока и формула Робинсона

Рис. 3. Линейная регрессия Индекс Бока и вес рассчитаны с идеальным ИМТ.

При сравнении с учетом различных диапазонов роста, <140 см, 141-150, 151-160, 161-170, 171-180,> 1,81, мы не обнаружили различий между обеими группами, но незначительные диапазоны роста, как правило, имеют меньшую корреляцию с BI, а диапазоны> 160 см имеют корреляцию более 50%.

Обсуждение

Наиболее часто используемыми антропометрическими показателями, используемыми в клинической практике для первоначальной оценки состояния питания человека, являются вес и рост.Они просты, практичны и легко достаются. Расчет IBW пациента ведется давно. В середине 19-го, ^{-го и} -го века, бельгийский астроном Кетле разработал индекс, показывающий, что масса тела у взрослых связана с квадратным ростом в постоянной зависимости. Несколько лет спустя, в 1871 году, французский хирург Пьер Брока, пионер в области физической антропологии и известный своими многочисленными работами по антропометрии мозга и черепа, ввел в клиническую практику индекс, носящий его имя, для определения этого важного параметра, полученного у взрослых. эмпирически путем вычитания 100 см из роста пациента [3-5].

Исторически IBW определялась как ассоциированная с самой низкой смертностью, поэтому она имеет большое значение. Согласно актуарным данным страховщиков, полученным в результате оценки веса и роста большого количества здорового населения, были созданы диаграммы для получения IBW. Первая задокументированная таблица была опубликована в 1913 году компанией Medico-Actuarial Mortality Investigation, а впоследствии, в 1942 году, Metropolitan Life Insurance Company выпустила свои собственные таблицы, основанные на продолжительности жизни [6,7].Из-за непрактичности эти таблицы были заменены уравнениями для оценки идеального веса.

В 1963 и 1964 годах Хамви [8] и Девайн [9] разработали и опубликовали формулы для расчета IBW для получения соответствующих доз определенных лекарств. С тех пор несколько похожих формул и уравнений были созданы для той же цели посредством регрессионного анализа данных о весе и росте, например, уравнение Робинсона [10] в 1983 году, разработанное с той же целью.В том же году Miller et al. [11] также сформулировали другие уравнения на основе таблиц Metropolitan Life Insurance Company. Совсем недавно, в 2000 году, Хаммонд [12] создал версию метрической системы на основе уравнения Хамви.

Только в конце 1970-х годов было высказано предположение, что ИМТ предпочтительнее других весовых индексов для оценки IBW [13]. Поскольку вес взрослого увеличивается пропорционально квадрату роста, ИМТ имеет хорошую корреляцию с жировой массой со значениями r 0.7 в популяционных исследованиях. Первостепенное исследование Грея в 1989 году показало, что в популяции 750000 человек диапазон ИМТ от 20 до 25 кг / м ² был тем, который лучше коррелировал с более низким уровнем смертности, и что он экспоненциально увеличивался по мере увеличения, становясь все более значительным. 200% у пациентов с ИМТ> 40 кг / м ² [13-16]. Таким образом, ИМТ также использовался в качестве критерия для определения желаемого диапазона веса и признан на международном уровне как Всемирной организацией здравоохранения (ВОЗ), так и Национальными институтами здравоохранения (NIH), определяя различные интервалы для классификации пациентов как пациентов с избыточным весом, ожирением I. , II, патологическое ожирение или выше [16].

Любое из приведенных выше уравнений, а также идеальный ИМТ можно использовать для расчета IBW, однако их нелегко использовать в повседневной клинической практике без калькулятора и требует времени.

Некоторые авторы подчеркивают, что в этом отношении необходимо провести более глубокий анализ и что мы должны забыть как IBW, так и BMI из-за недостатка, заключающегося в том, что они не различают жировую массу от массы без жира [12], однако исследования, которые проанализировать состав тела и предоставить нам эти данные, они более дороги и недоступны в повседневной клинической практике.

Shan et al [1] составили список формул IBW, используемых для оценки взаимосвязи между таблицами роста и веса и уравнениями IBW, а также для определения того, какая формула или таблица лучше всего подходят для ИМТ 22 кг / м. ² с использованием линейных регрессии и корреляции, обнаружив, что большинство наклонов формул попадают в диапазон ИМТ от 20 до 25 кг / м ² , с различиями между мужчинами и женщинами, поэтому они предложили использовать формулы в качестве руководства для тела осла веса, а не оценки веса из различных таблиц роста и веса.

Наше исследование было направлено на оценку достоверности BI. Мы хотели узнать, есть ли различия между уравнениями Хаммонда и Робинсона и весом, рассчитанным исходя из идеального ИМТ 22,5 кг / м 2 ^2, , и оценить, есть ли различия между тучной и не страдающей ожирением популяцией, а также между мужчинами и женщинами. женщин и разных уровней роста, поэтому мы разделили пациентов на две группы в соответствии с их ИМТ более или менее 30 кг / м ² и проанализировали данные отдельно между мужчинами и женщинами и разными диапазонами роста, чтобы проверить, есть ли разница. между этими группами у здоровых взрослых.Мы не включали детей, поскольку полезность этого индекса ограничена взрослым населением. При сравнении BI с другими тремя формулами, использованными в этом исследовании, сравнительный анализ с использованием статистики t-Стьюдента и корреляции Пирсона имел статистическую значимость в обеих группах (p 0,000). При использовании линейной регрессии при сравнении всех упомянутых формул было получено значение 100% (R2 1000), что, кажется, подтверждает, что BI имеет ту же точность, что и другие три уравнения, и может использоваться для этого предложения с уверенностью независимо от вес, ИМТ и рост у взрослых.Когда мы сравнивали разные диапазоны роста, мы обнаружили, что более высокие диапазоны BI имеют большую корреляцию, чем более низкие.

Заключение

Кажется, что BI предлагает ту же точность, что и другие более сложные формулы, такие как Хаммонда и Робинсона для расчета IBW, а также хорошо коррелирует с весом, рассчитанным на основе идеального BMI, и что он продолжает иметь валидность и полезность в клинической практике. , поэтому мы продвигаем его использование в клинической практике ввиду его простоты и практичности.

Конфликт интересов

Авторы, вовлеченные в это расследование, заявляют, что у них нет конфликта интересов.

Вклад авторов

Д-р Алехандро Вебер: Концепция и план расследования. Главный автор, главный рецензент и исследователь. Генеральный супервайзер.

Лиц. София Ортега: Исследователь и рецензент, Сбор данных и анализ.

Д-р Пабло Вебе2021 Авторские права OAT. Все права защищены, рецензент, Статистический анализ и интерпретация данных.

Список литературы

1. Shah B, Sucher K, Hollenbeck CB (2006) Сравнение уравнений идеальной массы тела и опубликованных таблиц роста и веса с таблицами индекса массы тела для здоровых взрослых в Соединенных Штатах. Орех Clin Pract 21: 312-319.
2. Беррингтон де Гонсалес А., Хартге П., Серхан Дж. Р., Флинт А. Дж., Ханнан Л. и др.(2010) Индекс массы тела и смертность 1,46 миллиона взрослых белых. N Engl J Med 363: 2211-2219. [Crossref]
3. Peterson CM, Thomas DM, Blackburn GL, Heymsfield SB (2016) Универсальное уравнение для оценки идеальной массы тела и массы тела при любом ИМТ. Am J Clin Nutr 103: 1197-1203. [Crossref]
4. Pai MP, Paloucek FP (2000) Происхождение «идеальных» уравнений веса тела. Ann Pharmacother 34: 1066-1069.[Crossref]
5. Rössner S (2007) Поль Пьер Брока (1824-1880). Obes Rev 8: 277. [Crossref]
6. Metropolitan Life Insurance Company (1942) Идеальные веса для мужчин. Stat Bull Metrop Life Insur Co 23: 6–8.
7. Metropolitan Life Insurance Company (1943) Идеальный вес для женщин. Stat Bull Metrop Life Insur Co 24: 6–8.
8. Hamwi GL. (2033) Изменение диетических концепций терапии.В: Дановский Т.С., редактор. Сахарный диабет: диагностика и лечение, Нью-Йорк: Американская диабетическая ассоциация, стр. 73-8.
9. Devine BJ (1974) Гентамициновая терапия. Лекарство Intell Clin Pharm 8: 650–655.
10. Робинсон Дж. Д., Лупкевич С. М., Паленик Л., Лопес Л. М., Ариет М. (1983) Определение идеальной массы тела для расчета дозировки лекарств. Am J Hosp Pharm 40: 1016-1019. [Crossref]
11. Miller DR, Carlson JD, Lloyd BJ, Day BJ (1983) Определение идеального тела? вес (и масса). Am J Hosp Pharm 40: 1622–1625.
12. Hammond KA. (2000) Диетическая и клиническая оценка. В: Махан Л.К., Пень С.Е., редакторы. Краузе о еде, питании и диетотерапии. (11-е издание), Сондерс, Филадельфия, стр. 353–79.
13. Müller MJ1 (2016) Идеальная масса тела или ИМТ: так что же это должно быть? Am J Clin Nutr 103: 1193-1194. [Crossref]
14. Flegal KM, Kit BK, Orpana H, Graubard BI (2013) Связь общей смертности с избыточным весом и ожирением с использованием стандартных категорий индекса массы тела: систематический обзор и метаанализ. JAMA 309: 71-82. [Crossref]
15. Wang ZJ, Zhou YJ, Galper BZ и др. (2015) Связь индекса массы тела со смертностью и сердечно-сосудистыми событиями для пациентов с ишемической болезнью сердца: систематический обзор и метаанализ. Сердце 101: 1631-1638.
16. Gray DS (1989) Диагностика и распространенность ожирения. Med Clin North Am 73: 1-13.
17. Hruby A, Hu FB (2015) Эпидемиология ожирения: общая картина. Фармакоэкономика 33: 673-689. [Crossref]

Калькулятор BloodSTAR для корректировки дозы Ig для идеальной массы тела

Корректировка дозы иммуноглобулина для идеальной массы тела

Количество иммуноглобулина (Ig), назначаемое пациенту, может варьироваться в зависимости от показаний, а также веса пациента и указано в Критериях клинического использования иммуноглобулина в Австралии (Критерии). При назначении Ig врачи должны стремиться использовать наименьшую возможную дозу, которая обеспечивает соответствующий клинический результат для каждого пациента.Считается, что этот подход не только сохраняет использование этого ценного продукта, но и потенциально снижает побочные эффекты, некоторые из которых могут быть связаны с дозой.

Клиницисты, назначающие Ig, могут корректировать дозу для достижения идеальной массы тела (IBW) по своему усмотрению или в соответствии с политикой штата / территории. Этот подход чаще всего применяется, когда пациент значительно страдает избыточным весом или ожирением из-за фармакокинетических свойств Ig. Исследования показали, что Ig распределяется в жидкостях организма и очень мало распространяется в жировые отложения.Доза Ig, рассчитанная для пациентов с ожирением, должна учитывать повышенное распределение из-за избытка жидкости в организме без учета увеличения жира в организме ¹ . Хотя есть некоторые доказательства, подтверждающие корректировку дозы Ig с использованием расчетов идеальной массы тела у пациентов с ожирением, необходимы дальнейшие исследования в этой области.

В BloodSTAR имеется калькулятор, который помогает врачам корректировать дозу Ig для достижения идеальной массы тела.

Калькулятор BloodSTAR применяет два вычисления ² для получения веса для целей дозирования.

Расчет 1 — идеальная масса тела (IBW) (кг) (также известная как формула Девайна):

IBW для мужчин = 50 + [2,3 x (рост в дюймах * — 60)]

IBW для женщин = 45,5 + [2,3 x (рост в дюймах * — 60)]

* Введенный рост пациента будет преобразован из сантиметров в дюймы для соответствия формуле. 1 сантиметр эквивалентен 0,393701 дюйму.

Расчет 2 — Вес для определения дозы (DDW) (кг):

DDW = IBW + 0.4 x (фактическая масса тела в кг — IBW)

НБА не рекомендует применять калькулятор пациентам:

• в возрасте до 18 лет;
• ростом менее 152 см; или
• беременных.

Кроме того, если калькулятор применяется, но фактический вес пациента меньше веса, определенного дозой (DDW) (рассчитанного в BloodSTAR), доза Ig должна быть рассчитана с использованием фактического веса пациента .

^{1.Сигел, Дж. (2010, январь). IVIG FAQ: иммуноглобулины и ожирение. Новости аптечной практики, стр. 8-9.}
2. Пай, М.П. И Палоучек, Ф. (2000). Происхождение «идеальных» уравнений веса тела. Анналы фармакотерапии, 34 (9), 1066-9.

Числа индекса массы тела (ИМТ) и уровни ожирения

«Единственный способ снизить ИМТ — это снизить массу тела, поскольку взрослые обычно не становятся выше, чтобы снизить свой ИМТ», — говорит Латеган-Потгитер. По данным MedlinePlus, даже небольшая потеря веса — от 5 до 10 процентов от общей массы тела — может значительно снизить риск заболеваний, связанных с ожирением.(20) По данным Национального института диабета, болезней пищеварительной системы и почек (NIDDK), этого может быть все, что нужно для снижения уровня сахара в крови, артериального давления и триглицеридов. (21)

Начните со здорового питания и физических упражнений. «Лучшая диета — это та, которую можно превратить в долгосрочный образ жизни», — говорит Скуит. Не существует диеты, которая лучше всего подходит для всех, но Скуит говорит, что самые успешные диеты обычно включают овощи, составляющие одну треть или половину приема пищи, и большое количество воды.Крихели предлагает встретиться с диетологом, который подберет для вас лучший подход.

Упражнения тоже важны. Американская кардиологическая ассоциация рекомендует заниматься не менее 150 минут упражнений средней интенсивности или 75 минут энергичной аэробной активности в неделю. (22) Если вы только начинаете, начните медленно с примерно 30 минут в день упражнений с низкой интенсивностью, таких как ходьба, или разбейте эти 30 минут на три 10-минутных занятия, если это кажется слишком большим, говорит Скуит. Вы можете строить оттуда, когда станет легче.

Если смена диеты и режима упражнений не дает желаемых результатов и вы соответствуете клиническим требованиям, ваш врач может предложить бариатрическую операцию. По данным клиники Mayo, существует три типа — билиопанкреативная диверсия с переключением двенадцатиперстной кишки, желудочный обходной анастомоз и рукавная гастрэктомия. Все они связаны с изменением вашей пищеварительной системы, чтобы способствовать снижению веса. Эти операции обычно предназначены для людей с тяжелым избыточным весом (с ИМТ 40 или выше) или если ваш ИМТ составляет от 35 до 40, и вы также боретесь с проблемами со здоровьем, связанными с весом, такими как диабет 2 типа, высокое кровяное давление. давление или тяжелое апноэ во сне.(23)

Существуют также рецептурные лекарства, предназначенные для лечения ожирения путем снижения аппетита или уменьшения количества жира, усваиваемого организмом. Согласно NIDDK, некоторые распространенные лекарства для похудения, одобренные FDA: (21)

Лекарства могут быть вариантом, если у вас ИМТ 30 или выше или выше 27, а также есть проблемы со здоровьем, связанные с весом, говорит Крихели.

Имейте в виду, что операция, процедуры и лекарства не уменьшат ваш вес волшебным образом. «Ни одно из этих средств не является лекарством — это всего лишь лечение», — говорит Крихели.«Они не заменяют здоровый образ жизни, питание, упражнения и активность».

Дополнительная информация Энн Л.