«Формула» гоночного шлема: есть ли прорехи?
- Катя Москвич
- bbcrussian.com
Фелипе Масса надеется вернуться в форму к новому сезону
Автогонщик команды Ferrari Фелипе Масса вернется на трассу уже в следующем сезоне, заявил в интервью bbcrussian.com представитель пресс-службы компании Лука Коладжанни.
По словам Коладжанни, Масса следил за последним Гран-при в Бельгии и победой своего напарника по команде Кими Райкконена по телевизору из Майами. Там он в понедельник прошел медицинское обследование у известного нейрохирурга Стива Олви.
Именно после благоприятного прогноза врачей руководство Ferrari решилось объявить, что мир автоспорта не потеряет одного из сильнейших гонщиков и Масса вернется в команду уже в 2010 году.
Бразильцу еще предстоит перенести операцию на черепе, однако в интервью пресс-службе Ferrari он сообщил, что успешный медосмотр его чрезвычайно обнадежил. «Я очень рад этим результатам», — признался гонщик. «После небольшой операции я наконец вернусь в спортзал, чтобы войти в форму, а потом начну тренироваться на картинге».
«Я очень рад этим результатам», — признался гонщик. «После небольшой операции я наконец вернусь в спортзал, чтобы войти в форму, а потом начну тренироваться на картинге».
Коладжанни также рассказал, что Масса постоянно поддерживает связь с командой и болеет за своего напарника Райкконена, который принес в воскресенье первую победу Ferrari в этом году. «Фелипе очень обрадовался победе Кими, ведь он отлично знает, как мы хотели выиграть хотя бы одну гонку в этом настолько трудном для нас сезоне», — сказал Коладжанни.
Несбывшиеся надежды
В прошлом году Масса окончил сезон в ранге вице-чемпиона, да и в течение прошлых лет Ferrari была, пожалуй, самой успешной командой «Формулы-1».
Однако этот сезон, в связи с новым регламентом, определенным Международной федерацией автоспорта FIA, оказался полон сюрпризов. Болиды нужно было конструировать практически с нуля, и вперед вырвались молодые команды вроде Brawn GP и Red Bull, а Ferrari сначала оказалась немного не у дел.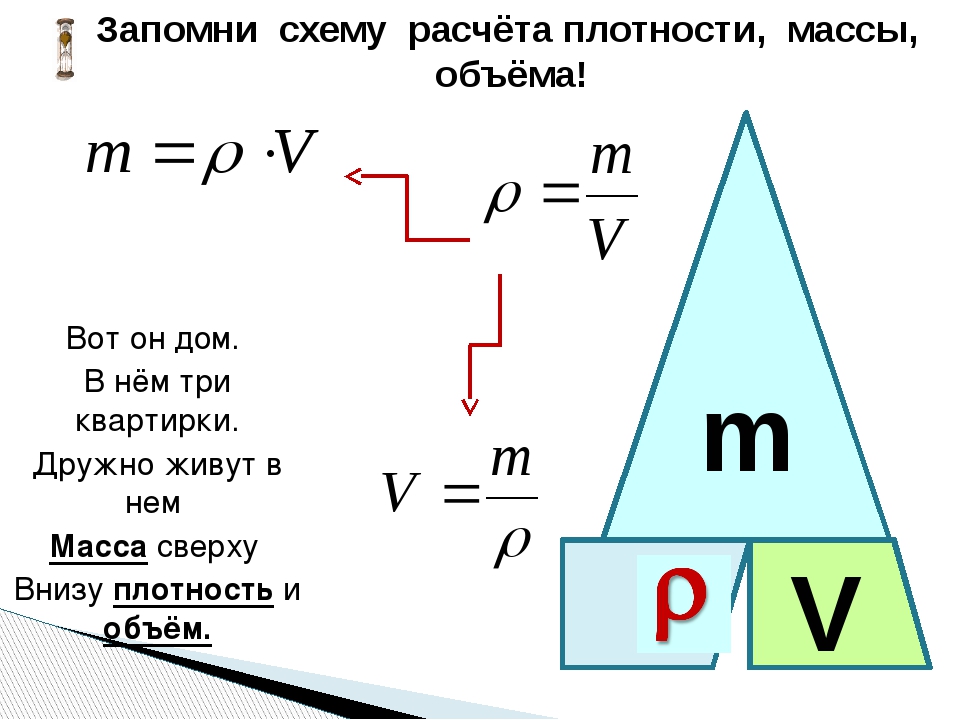
Но талант 28-летнего Массы никуда не исчез, ведь не зря в январе этого года глава «Формулы-1» Берни Экклстоун выразил надежду, что пилот в нынешнем сезоне получит заслуженный титул чемпиона.
Однако этому не суждено сбыться. Злополучная пружина, отскочившая от болида Рубенса Баррикелло на трассе в Будапеште, пробила шлем гонщика Ferrari и врезалась ему в голову на скорости 260 км/ч.
Результатом этой аварии стали тяжелая черепная травма, ряд сложнейших операций и то, что Масса вынужден сидеть перед телевизором, а не принимать участие в гонках — в первый раз за последние шесть лет.
Сразу после аварии Экклстоун заявил, что необходимо улучшить меры безопасности головной защиты автогонщиков: «Возможно, мы сможем поучиться у других видов спорта. Например, вратарям в хоккее необходим хороший обзор, и все же забрала их касок достаточно прочны, чтобы выдержать попадание летящей, как пуля, шайбы».
Тем не менее, Коладжанни полагает, что даже если Массу и спас его шлем, «стандарты безопасности всегда можно улучшить».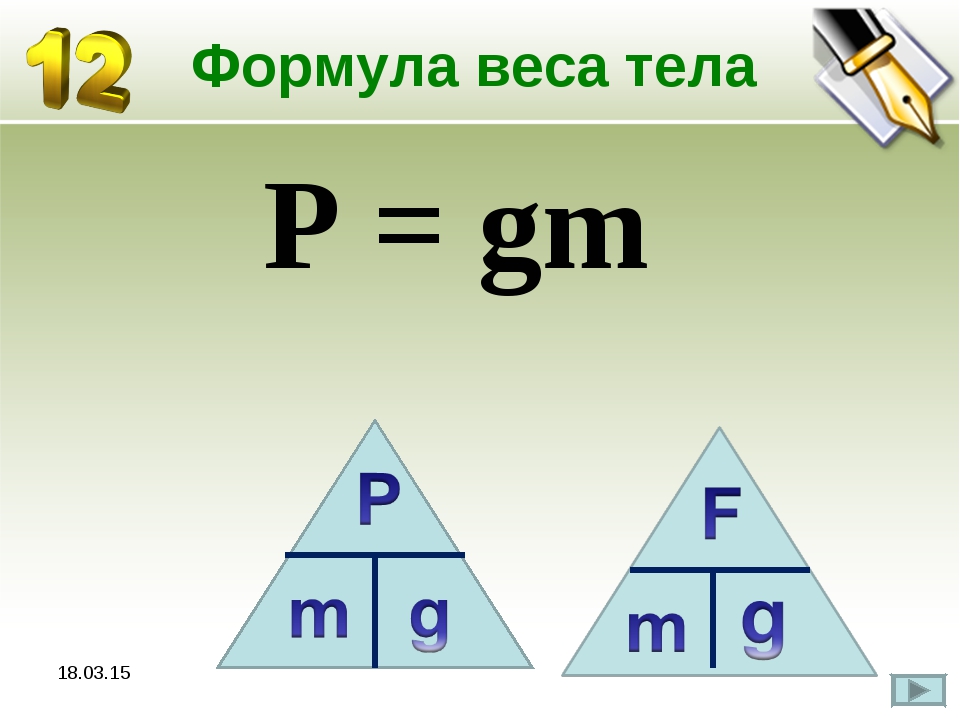
«Бразильский волшебник»
Подпись к фото,По мнению инженеров, сплошной кокпит слишком видоизменит традиционно открытый болид
Согласно пресс-релизу FIA, нынешние системы головной защиты прочнее их предшественников. Модель, которая была у гонщика Ferrari в момент аварии, изготовлена из прочного углепластика и была введена в эксплуатацию четыре года назад.
Ее образец был разработан согласно требованиям FIA 2004 года, ужесточенных после смерти знаменитого «Бразильского волшебника» Айртона Сенны.
То, что произошло с Массой, неприятно перекликается с аварией Сенны 15 лет назад: на пятом круге трассы Сан-Марино сломанный рычаг подвески на огромной скорости пробил его шлем, болид бразильца потерял управление и влетел в бетонную стену заграждения. Некоторое время спустя Сенны не стало.
Это происшествие заставило FIA призадуматься, и головные защиты были усовершенствованы. Однако авария, произошедшая с Массой, а также трагическая смерть 18-летнего пилота «Формулы-2» Генри Сертиса, случившаяся за несколько дней до этого, вновь вывели вопрос о безопасности пилотов в число актуальных.
По сообщению пресс-службы FIA, президент федерации Макс Мосли распорядился, чтобы комитет безопасности этой организации приготовил детальный отчет об обеих авариях и предложил рекомендации касательно улучшения мер безопасности в «Формуле-1».
Регламент FIA менялся уже не раз, и, согласно ему, видоизменялась форма болидов – вокруг кокпита и шасси появлялись различные нововведения, предназначенные для большей безопасности пилота.
В начале 2000-х команды начали устанавливать технологию HANS — систему защиты головы и шеи, благодаря которой значительно снижается нагрузка и вероятность повреждений шеи при сильных перегрузках и авариях. С 2008 года FIA сделала использование HANS обязательным.
Эксперты полагают, что именно благодаря этой технологии остался жив поляк Роберт Кубица, когда попал в аварию на трассе в Монреале в 2007 году. Будь она установлена, возможно, HANS могла бы спасти и Роланда Раценберга, который за день до гибели Сенны во время квалификаций врезался в отбойник на скорости 314 км/ч и вскоре скончался, так и не придя в сознание.
Безопасность и традиции
У Массы была и система HANS, и всевозможные защитные ограждения вокруг кокпита, благодаря которым, врезавшись в стену автопокрышек, пилот не получил еще больших переломов.
Однако его голова, хоть и в шлеме, осталась уязвимой, и именно поэтому некоторые эксперты полагают, что было бы разумней сделать сплошные кабины, чтобы гонщик полностью находился внутри машины. Но многие с этим не согласны, утверждая, что в этом случае у пилотов ухудшится обзор, а при аварии будет сложнее выскочить — или быть вытащенным — из болида.
Кроме того, есть еще одно возражение: как отметил один из инженеров команды Red Bull, сплошной кокпит настолько видоизменит традиционно открытую машину, что «Формула-1» потеряет свою индивидуальность.
А индивидуальность для многих любителей этого вида спорта даже важнее, чем безопасность.
IV. Определение массы вредных (загрязняющих) веществ, сброшенных со сточными водами и поступивших иными способами в водные объекты / КонсультантПлюс
IV.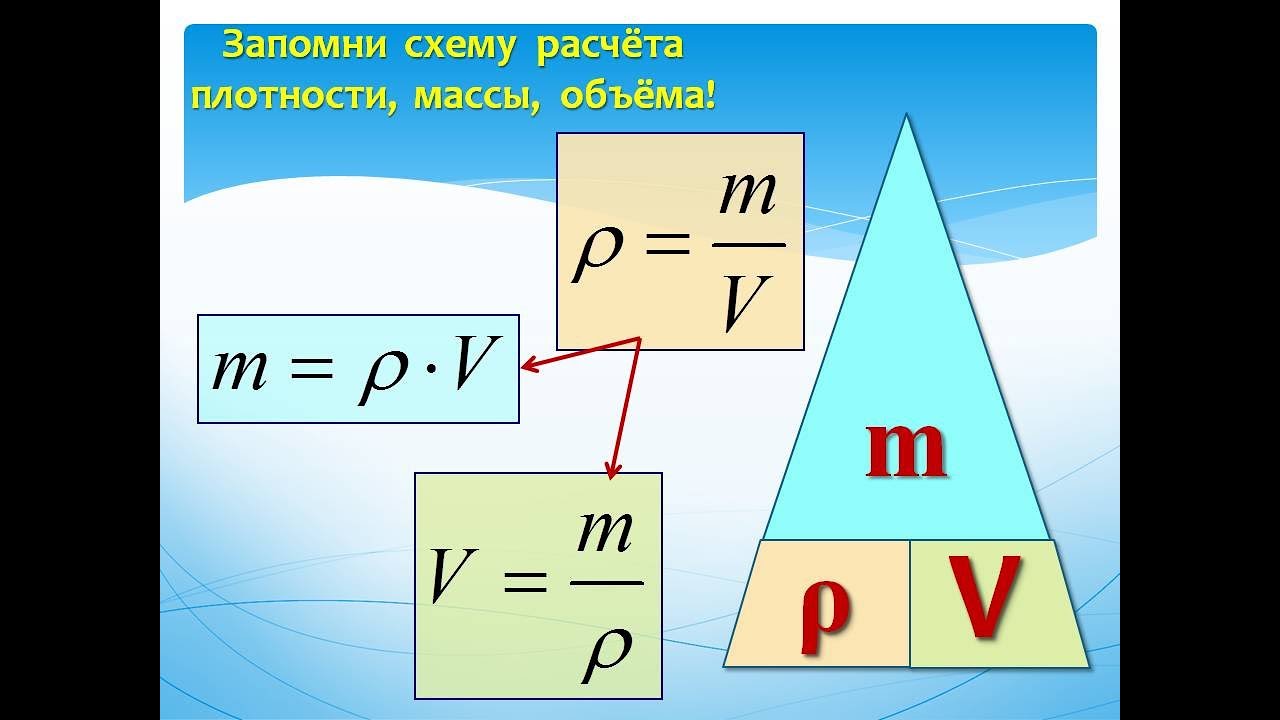 Определение массы вредных (загрязняющих) веществ,
Определение массы вредных (загрязняющих) веществ,
сброшенных со сточными водами и поступивших иными способами
в водные объекты
22. Масса сброшенного вредного (загрязняющего) вещества в составе сточных вод и (или) загрязненных дренажных (в том числе шахтных, рудничных) вод определяется по формуле N 10:
(в ред. Приказа Минприроды России от 31.01.2014 N 47)
-6
M = Q x (С — С ) x T x 10 , (10)
i фi дi
где: M — масса сброшенного i-го вредного (загрязняющего) вещества, т;
i
i — загрязняющее вещество, по которому исчисляется размер вреда;
Q — расход сточных вод и (или) загрязненных дренажных (в том числе шахтных, рудничных) вод, с превышением содержания i-го вредного (загрязняющего) вещества определяется по приборам учета, а при их отсутствии — расчетным путем в соответствии с методами расчета объема сброса сточных вод и их характеристик, м3/час;
(в ред. Приказа Минприроды России от 31.01.2014 N 47)
Приказа Минприроды России от 31.01.2014 N 47)
С — средняя фактическая за период сброса концентрация i-го вредного
фi
(загрязняющего) вещества в сточных водах и (или) загрязненных дренажных (в
том числе шахтных, рудничных) водах, определяемая по результатам анализов
аккредитованной лаборатории как средняя арифметическая из общего количества
результатов анализов (не менее 3-х) за период времени T, мг/дм3;
С — допустимая концентрация i-го вредного (загрязняющего) вещества в
дi
пределах норматива допустимого (предельно допустимого) сброса или лимита
сброса при его наличии на период проведения мероприятий по снижению сбросов
вредных (загрязняющих) веществ в водные объекты, мг/дм3.
Допустимая концентрация i-го вредного (загрязняющего) вещества в пределах норматива допустимого (предельно допустимого) сброса или лимита на сбросы при его наличии для организаций, осуществляющих водоотведение в соответствии с Федеральным законом «О водоснабжении и водоотведении», вносящих плату за негативное воздействие на окружающую среду, применяется с коэффициентом, равным 1,4 (кроме случаев аварийного и залпового сброса сточных вод).
(абзац введен Приказом Минприроды России от 26.08.2015 N 365)
В случае, если установлено, что фоновая концентрация i-го вредного (загрязняющего) вещества в воде водного объекта превышает допустимую концентрацию, для расчета применяется значение фоновой концентрации.
(абзац введен Приказом Минприроды России от 26.08.2015 N 365)
T — продолжительность сброса сточных вод и загрязненных дренажных (в том числе шахтных, рудничных) вод с повышенным содержанием вредных (загрязняющих) веществ, определяемая с момента обнаружения сброса и до его прекращения, час;
-6
10 — коэффициент перевода массы вредного (загрязняющего) вещества в
т.
22.1. При отсутствии данных о фактическом расходе или объеме сброшенных сточных вод, а также невозможности использования расчетного метода в соответствии с пунктом 22 настоящей Методики это количество может быть приравнено к расходу или объему воды, потребляемому организацией для целей питьевого и хозяйственно-бытового водоснабжения за период, равный периоду сброса сточных вод с превышением допустимых концентраций вредных (загрязняющих) веществ, которые установлены нормативом допустимого (предельно допустимого) сброса или лимитом сброса при его наличии.
Фактический объем сбрасываемых загрязненных дренажных (в том числе шахтных, рудничных) вод определяется по данным измерительной техники, работы насосно-силового и другого оборудования, объема сечения сбросных каналов, а при их отсутствии по данным документов, на основании которых возникает право пользования водными объектами.
В том случае если произошел аварийный сброс сточных вод и (или) загрязненных дренажных (в том числе шахтных, рудничных) вод на водосборные площади (овраг, балка и т.д.), то масса сброса загрязняющих веществ определяется по их концентрации в месте поступления аварийного (залпового) сброса в водный объект.
22.2. Продолжительность сброса вредных (загрязняющих) веществ при нарушении водного законодательства, в том числе при аварийных сбросах, определяется с момента его обнаружения и до момента прекращения сброса.
В случае если водопользователь извещает контролирующие органы о сбросе сточных вод и (или) дренажных (в том числе шахтных, рудничных) вод с превышением допустимых концентраций вредных (загрязняющих) веществ, которые установлены нормативом допустимого (предельно допустимого) сброса или лимитом сброса при его наличии, то период продолжительности сброса определяется с момента извещения.
За момент прекращения сброса принимается дата его фактического прекращения, устанавливаемого органом исполнительной власти, осуществляющим федеральный и (или) региональный государственный контроль и надзор за использованием и охраной водных объектов, по результатам выполнения водопользователем предписания об устранении нарушений, связанных с превышением допустимых концентраций вредных (загрязняющих) веществ, которые установлены нормативом допустимого (предельно допустимого) сброса или лимитом сброса при его наличии, подтверждаемого результатами анализов качества сбрасываемых сточных вод и (или) дренажных (в том числе шахтных, рудничных) вод, а также при необходимости анализов качества вод водного объекта.
В случае, если водопользователь извещает контролирующие органы о прекращении сброса сточных, в том числе дренажных (шахтных, рудничных), вод с превышением показателей, устанавливаемых в нормативах допустимых сбросов абонентов, лимитах на сбросы <7>, или в нормативах водоотведения (сброса) по составу сточных вод <8>, за момент прекращения сброса принимается дата такого извещения при условии подтверждения результатами лабораторных исследований, проведенных организацией, аккредитованной соответствии с законодательством Российской Федерации об аккредитации в национальной системе аккредитации факта, прекращения сброса сточных, в том числе дренажных (шахтных, рудничных), вод с превышением данных показателей.
(абзац введен Приказом Минприроды России от 26.08.2015 N 365)
———————————
<7> Нормативы допустимых сбросов абонентов, лимиты на сбросы устанавливаются в соответствии со статьями 26 и 27 Федерального закона «О водоснабжении и водоотведении».
(сноска введена Приказом Минприроды России от 26.08.2015 N 365)
<8> Нормативы водоотведения (сброса) по составу сточных вод устанавливаются в соответствии с Правилами холодного водоснабжения и водоотведения.
(сноска введена Приказом Минприроды России от 26.08.2015 N 365)
При повторном установлении факта нарушения в течение 5 рабочих дней с момента получения органом исполнительной власти, осуществляющим федеральный и (или) региональный государственный контроль и надзор за использованием и охраной водных объектов, информации о прекращении сброса и невыполнении нарушителем водного законодательства мероприятий по снижению концентраций вредных (загрязняющих) веществ в сбрасываемых сточных водах и (или) загрязненных дренажных (в том числе шахтных, рудничных) водах до установленных в первичном предписании, выданном органом исполнительной власти, осуществляющим федеральный и (или) региональный государственный контроль и надзор за использованием и охраной водных объектов, момент прекращения сброса устанавливается по данным лаборатории, привлеченной указанным органом исполнительной власти для проведения анализов качества сбрасываемых сточных вод и (или) дренажных (в том числе шахтных, рудничных) вод, а также при необходимости анализов качества вод водного объекта, или по данным отчета организации об устранении нарушений.
(в ред. Приказа Минприроды России от 31.01.2014 N 47)
22.3. При отсутствии документов, на основании которых возникает право
пользования водными объектами для сброса сточных вод и (или) дренажных (в
том числе шахтных, рудничных) вод, разрешений на сброс вредных
(загрязняющих) веществ в окружающую среду (водные объекты) при исчислении
размера вреда масса вредных (загрязняющих) веществ определяется по формуле
N 10, в которой концентрация i-го вредного (загрязняющего) вещества (С )
д
принимается равной фоновому показателю качества воды водного объекта.
При отсутствии количественного выражения указанного показателя в расчет принимается значение предельно допустимой концентрации вредного (загрязняющего) вещества в воде водного объекта в зависимости от установленного целевого использования водного объекта или его значения (назначения), а в случае одновременного использования водного объекта для различных целей или использования водного объекта, имеющего различные значения (назначения), принимаются наиболее жесткие нормы качества воды водного объекта из числа установленных.
23. Масса сброшенных в водный объект органических веществ, выраженная в
БПК в составе сточных вод и (или) загрязненных дренажных (в том числе
полн.
шахтных, рудничных) вод, определяется по формуле N 11:
ф д -6
М = Q x (С — С ) x T x 10 , (11)
БПКполн. БПКполн. БПКполн.
где: М — масса сброшенных органических веществ в БПК , т;
БПКполн. полн.
Q — расход сточных вод и (или) загрязненных дренажных (в том числе шахтных, рудничных) вод, поступающих на очистные сооружения, м3/час;
ф д
С , С — соответственно фактические и допустимые к сбросу
БПКполн. БПКполн.
концентрации органических веществ в сточных водах и (или) загрязненных
дренажных (в том числе шахтных, рудничных) водах, выраженные в БПК ,
полн.
мг/дм3;
T — продолжительность сброса сточных вод и (или) загрязненных дренажных (в том числе шахтных, рудничных) вод, с повышенной концентрацией органических веществ, определяемая с момента обнаружения сброса до его прекращения, час;
-6
10 — коэффициент перевода массы вредного (загрязняющего) вещества в
т.
23.1. Концентрация органического вещества в сточных водах и (или)
дренажных (в том числе шахтных, рудничных) водах, выраженная в БПК ,
полн.
определяется по формуле N 12:
С = С x К , (12)
БПКполн. орг.i бпк
где: С — концентрация органического вещества, выраженная в
БПКполн.
БПК ;
полн.
С — концентрация органического вещества, мг/дм3;
орг.i
К — коэффициент пересчета концентрации органического вещества в
бпк
соответствующую ему величину БПК , определяется в соответствии с
полн.
таблицей 14 приложения 1 к настоящей Методике.
23.2. При наличии данных о массе сброшенных органических веществ,
выраженной в БПК , производится пересчет этих данных в БПК по формуле
5 полн.
N 13:
М = М x 1,43, (13)
БПКполн. БПК5
где: М — масса сброшенных органических веществ, выраженная в БПК , т.
БПК5 5
24. Масса нефти, нефтепродуктов и других вредных (загрязняющих) веществ, попавших в водный объект, за исключением их сбросов в составе сточных вод и (или) загрязненных дренажных (в том числе шахтных, рудничных) вод, определяется следующими способами:
по результатам инструментальных измерений массы нефти, нефтепродуктов и других вредных (загрязняющих) веществ на единице площади и концентрации растворенных или находящихся во взвешенном состоянии под слоем воды разлива нефти, нефтепродуктов и других вредных (загрязняющих) веществ с учетом их фонового содержания в воде водного объекта;
по площади разлива, определенной с помощью инструментальных или визуальных методов;
по количеству нефти, нефтепродуктов и других вредных (загрязняющих) веществ, собранных нефтемусоросборными или другими средствами при ликвидации разлива нефти, нефтепродуктов и других вредных (загрязняющих) веществ с учетом их фонового содержания в воде водного объекта;
на основе оценок состояния акватории водного объекта и внешних признаков пленки нефти и нефтепродуктов в соответствии с таблицей 15 приложения 1 к настоящей Методике;
по балансу между количеством нефти, нефтепродуктов и других вредных (загрязняющих) веществ, вылившихся в водный объект из емкости с известным объемом и количеством нефти, нефтепродуктов и других вредных (загрязняющих) веществ, оставшихся в емкости;
по показаниям измерительных приборов, используемых при производстве погрузочно-разгрузочных операций;
по результатам непосредственных замеров в соответствующих емкостях судна.
В случае, если при определении массы сброшенных нефти, нефтепродуктов и других вредных (загрязняющих) веществ указанными способами получены различные результаты, в расчет включается средняя арифметическая величина.
24.1. Масса нефти, нефтепродуктов или других вредных (загрязняющих) веществ, поступивших в водный объект, рассчитанная методом инструментальных замеров, определяется по формуле N 14:
М = М + М , (14)
н нп рн
где: М — масса нефти, нефтепродуктов или других вредных (загрязняющих)
н
веществ, поступивших в водный объект, т;
М — масса пленки нефти, нефтепродуктов или других вредных
нп
(загрязняющих) веществ, поступивших в водный объект, т;
М — масса растворенных и (или) эмульгированных в воде водного объекта
рн
нефти, нефтепродуктов или других вредных (загрязняющих) веществ, т.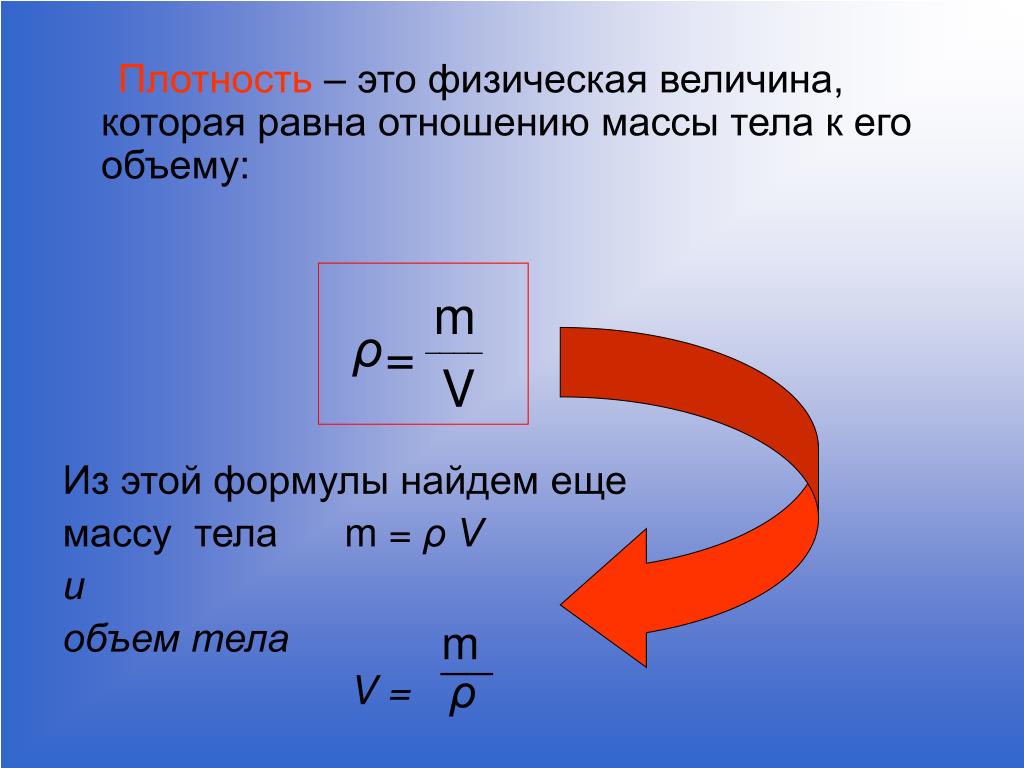
Масса пленки нефти, нефтепродуктов или других вредных (загрязняющих) веществ определяется по формуле N 15:
-6
М = УМ x S x 10 , (15)
нп н
где: УМ — масса пленки нефти, нефтепродуктов или других вредных
н
(загрязняющих) веществ на 1 м2 акватории водного объекта, г/м2;
S — площадь акватории водного объекта, покрытая разлитой нефтью, нефтепродуктами или другими вредными (загрязняющими) веществами, м2;
-6
10 — коэффициент перевода массы вредных (загрязняющих) веществ в т.
Масса растворенных и (или) эмульгированных в воде водного объекта нефти, нефтепродуктов или других вредных (загрязняющих) веществ определяется по формуле N 16:
-6
М = С x V x 10 , (16)
рн рн
где: С — средняя (из анализов в 4 — 6 точках разлива) концентрация
рн
растворенных и (или) эмульгированных в воде водного объекта нефти,
нефтепродуктов или других вредных (загрязняющих) веществ под слоем разлива
на глубине до 1 м, мг/дм3. В случае обоснованной невозможности определения
В случае обоснованной невозможности определения
С инструментальным методом можно использовать показатели таблицы 16
рн
приложения 1 к настоящей Методике;
V — объем воды в водном объекте, загрязненной растворенными и (или) эмульгированными нефтью, нефтепродуктами или другими вредными (загрязняющими) веществами, м3, определяется по формуле N 17:
где: h — средняя (не менее 3-х измерений) глубина воды в водном объекте, загрязненной растворенными нефтью, нефтепродуктами и другими вредными (загрязняющими) веществами, определенная на основании протоколов лабораторных исследований, м;
S — площадь акватории водного объекта, загрязненной разлитой нефтью, нефтепродуктами или другими вредными (загрязняющими) веществами, м2;
-6
10 — коэффициент перевода массы вредных (загрязняющих) веществ в т.
24.2. Масса пленки нефти, нефтепродуктов в воде водного объекта, определяемая по методу оценок состояния акватории водного объекта и внешних признаков пленки при толщине слоя нефти, нефтепродуктов в месте разлива меньше 1 мм, рассчитывается по формуле N 18:
-6
М = УМ x S x 10 , (18)
нп н
где: УМ — удельная масса нефти, нефтепродуктов на 1 м2 акватории
н
водного объекта, определяется в соответствии с таблицей 15 приложения 1 к
настоящей Методике, г/ м2;
S — площадь акватории водного объекта, покрытой разлитой нефтью, нефтепродуктами, м2;
-6
10 — коэффициент перевода массы вредных (загрязняющих) веществ в т.
24.3. Масса нефти, нефтепродуктов, поступивших в водный объект, определяемая по количеству собранной нефти и нефтепродуктов нефтемусоросборными средствами при ликвидации разлива, рассчитывается следующим образом.
Если известна масса собранной нефтемусоросборными средствами нефти и нефтепродуктов, то общее количество нефти и нефтепродуктов, поступивших в водный объект, определяется суммированием массы собранных нефти, нефтепродуктов и нефти, нефтепродуктов, оставшихся в водном объекте после проведения работ по ликвидации разлива, включая пленки нефти, нефтепродуктов и растворенные в воде водного объекта.
Масса нефти, нефтепродуктов, попавших в водный объект, определяемая по балансу между количеством нефти, нефтепродуктов, вылившихся в водный объект из емкости с известным объемом и количеством нефти, нефтепродуктов, оставшихся в емкости, рассчитывается по формуле N 19:
М = М — М , (19)
н нис ност
где: М — масса нефти, нефтепродуктов, поступивших в водный объект, т;
н
М — исходная масса нефти, нефтепродуктов, находившихся в емкости с
нис
известным объемом, т;
М — масса нефти, нефтепродуктов, оставшихся в емкости с известным
ност
объемом, т.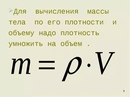
В случае разлива нефти и нефтепродуктов при производстве погрузочно-разгрузочных работ, когда их перекачиваемое количество фиксируется приборами, масса сброшенных нефти и нефтепродуктов устанавливается по разности показаний измерительных приборов и фактического наличия нефти, нефтепродуктов в соответствующих емкостях судна.
25. Тоннаж (масса) брошенных, полузатопленных и затопленных судов, других плавучих средств и крупногабаритных отходов производства и потребления (предметов) определяется по данным, полученным из актов инженерно-водолазного обследования судов, других плавучих средств и иных крупногабаритных отходов производства и потребления (предметов), актов освидетельствования судна, документов, содержащих инженерно-технические характеристики судна, другого плавучего средства и иных крупных предметов.
26. Объем накопления хозяйственно-бытовых сточных вод для судов первой категории (длиной свыше 65 м) принимается 50 литров, а для судов всех остальных категорий (длиной до 65 м) 25 литров на одного человека в сутки.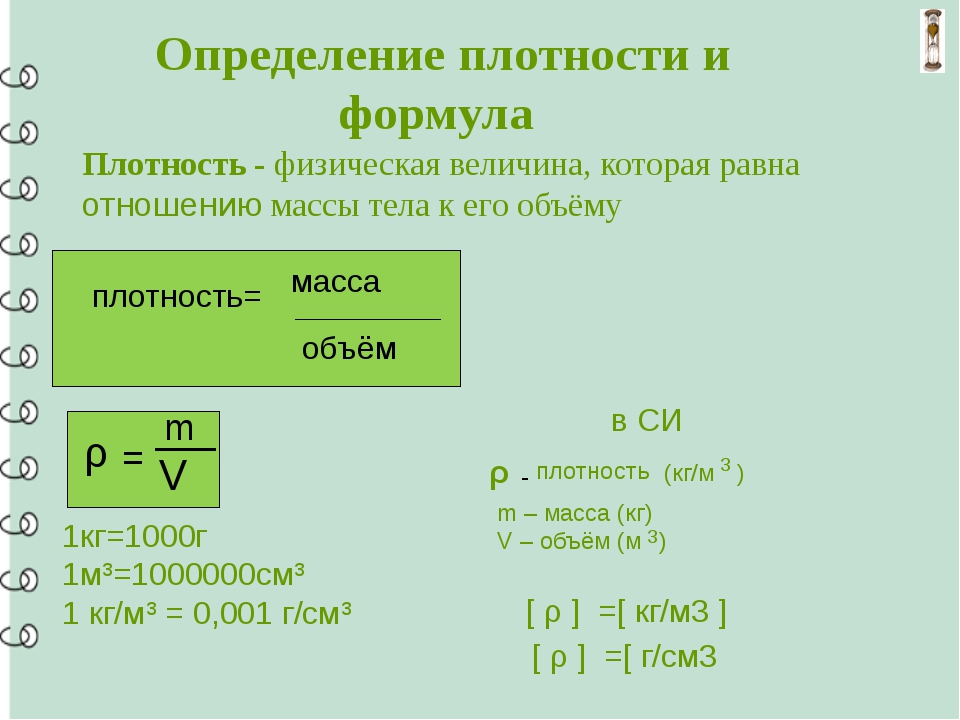
Расчетный объем накопления хозяйственно-бытовых сточных вод определяется по формуле N 20:
расч. -3
Q = q x n x t x 10 , (20)
ф ф
расч.
где: Q — расчетный объем хозяйственно-бытовых сточных вод за время
ф
непрерывного нахождения судна во внутренних и территориальных водах, м3;
q — объем хозяйственно-бытовых сточных вод, приходящийся на 1
ф
человека в сутки, л/сут./чел.;
n — количество находящихся на судне людей;
t — число суток непрерывного нахождения судна во внутренних и территориальных водах вне мест стоянок;
-3
10 — коэффициент перевода объема вредных (загрязняющих) веществ в м3.
Приведенное количество емкостей накопления определяется по формуле N 21:
расч.
N = Q /q , (21)
прив ф N
где: q — средний объем емкости накопления хозяйственно-бытовых сточных
N
вод на судне аналогичного класса, м3.
27. Масса взвешенных веществ при проведении работ в водном объекте и при разрушении в результате аварий гидротехнических и иных сооружений на водных объектах, указанных в пункте 19 настоящей Методики, определяется по формуле N 22:
-6
М = S x H x (С — С ) x 10 , (22)
взв акв ср ср ф
где: М — масса взвешенных веществ при проведении работ в водном
взв
объекте и при разрушении в результате аварий гидротехнических и иных
сооружений на водных объектах, т;
S — площадь загрязненной акватории водного объекта, в м2,
акв
определяемая по формуле N 23:
S = L x B , (23)
акв ср ср
где: L — средняя (не менее 3-х измерений) длина распространения
ср
взвешенных веществ на акватории водного объекта, м;
B — средняя (не менее 3-х измерений) ширина распространения
ср
взвешенных веществ на акватории водного объекта, м;
H — средняя (не менее 3-х измерений) глубина распространения
ср
взвешенных веществ в акватории водного объекта, м.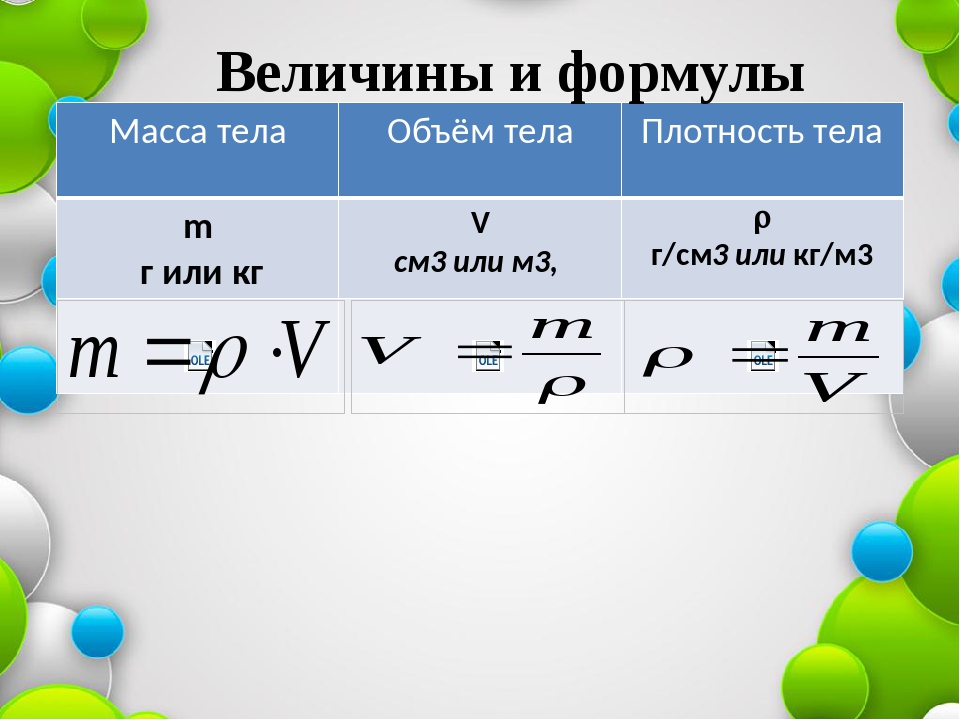
Измерения производятся на глубине до 1 м;
С — средняя (не менее 3-х анализов) концентрация взвешенных веществ,
ср
содержащихся в воде загрязненной акватории водного объекта, мг/дм3;
С — фоновая концентрации взвешенных веществ в воде акватории водного
ф
объекта, мг/дм3;
-6
10 — коэффициент перевода массы взвешенных веществ в т.
28. Масса вредных (загрязняющих) веществ от несанкционированных (запрещенных) сбросов вредных (загрязняющих) веществ, отходов производства и потребления, включая отходы перерабатывающей и пищевой промышленности, отходы содержания животных и птиц, в том числе отходы птицефабрик (птицеферм) и другие отходы, производственные отвалы некондиционных руд, удобрения, ядохимикаты и другие вещества, хранящиеся открытым способом в водоохранной зоне водного объекта или на водосборной площади, смываемых дождевыми, талыми водами в водные объекты, определяется по формуле N 24:
-6
М = S x (С О + С О ) x 10 , (24)
нсi дi д тi т
где: М — масса сброса i-го вредного (загрязняющего) вещества,
нсi
смываемого дождевыми и талыми водами, т;
S — площадь водоохраной зоны водного объекта или водосборная площадь, занятая вышеперечисленными вредными (загрязняющими) веществами, включая площадь водонепроницаемых покрытий, га;
О , О — объемы стока соответственно дождевых и талых вод за время (t)
д т
сброса, м3/га;
С , С — средние (не менее 3-х анализов) концентрации i-го вредного
дi тi
(загрязняющего) вещества соответственно в дождевых и талых водах, мг/дм3.
28.1. Общая площадь водоохраной зоны водного объекта или водосборная площадь, включая площадь водонепроницаемых покрытий, на которой расположены вредные (загрязняющие) вещества, перечисленные в пункте 28 настоящей Методики, определяется по данным генерального плана землеустройства и (или) данным государственной статистической отчетности об использовании земель, по данным конкретных измерений или экспертной оценки.
28.2. Объем стока дождевых вод определяется по формуле N 25:
О = 2,5 x H x К x К x К , (25)
д д q вн t
где: О — объем стока дождевых вод, м3/га;
д
H — слой осадков за теплый период (апрель — октябрь) со средними
д
температурами выше 0 °C определяется по данным метеорологических
наблюдений, мм;
К — коэффициент, учитывающий объем стока дождевых вод в зависимости от
q
интенсивности дождя для данной местности продолжительностью 20 минут при
периоде однократного превышения расчетной интенсивности дождя, равном 1
году (q ), определяется по данным нижеприведенной таблицы, для которой
20
значение q принимается в соответствии с рисунком 1 приложения 2
20
к настоящей Методике:
┌─────┬──────┬──────┬─────┬──────┬──────┬───────┬─────┬─────┬───────┬─────┐
│ q │ 20 │ 30 │ 40 │ 50 │ 60 │ 70 │ 80 │ 90 │ 100 │ 120 │
│ 20 │ │ │ │ │ │ │ │ │ │ │
├─────┼──────┼──────┼─────┼──────┼──────┼───────┼─────┼─────┼───────┼─────┤
│ К │ 0,96 │ 0,91 │ 0,87│ 0,82 │ 0,78 │ 0,75 │ 0,71│0,68 │ 0,65 │ 0,60│
│ q │ │ │ │ │ │ │ │ │ │ │
└─────┴──────┴──────┴─────┴──────┴──────┴───────┴─────┴─────┴───────┴─────┘
К — коэффициент, учитывающий интенсивность формирования дождевого
вн
стока с учетом удельного веса (в процентах) водонепроницаемых поверхностей
на площади водоохраной зоны водного объекта или водосборной площади, на
которой расположены вредные (загрязняющие) вещества, перечисленные в пункте
28 настоящей Методики, определяется по данным нижеприведенной таблицы:
┌────────┬──────┬─────┬─────┬─────┬─────┬─────┬─────┬───────┬──────┬──────┐
│ П , % │ 10 │ 20 │ 30 │ 40 │ 50 │ 60 │ 70 │ 80 │ 90 │ 100 │
│ вн │ │ │ │ │ │ │ │ │ │ │
├────────┼──────┼─────┼─────┼─────┼─────┼─────┼─────┼───────┼──────┼──────┤
│ К │ 0,4 │ 0,6 │ 0,8 │ 1,0 │ 1,2 │ 1,4 │ 1,6 │ 1,8 │ 2,0 │ 2,2 │
│ вн │ │ │ │ │ │ │ │ │ │ │
└────────┴──────┴─────┴─────┴─────┴─────┴─────┴─────┴───────┴──────┴──────┘
К — коэффициент, учитывающий принимаемое к расчету размера вреда время
t
сброса вредных (загрязняющих) веществ по отношению к продолжительности
теплого периода.
28.3. Объем стока талых вод определяется по формуле N 26:
О = H x К x К , (26)
т т т t
где: О — объем стока талых вод, м3/га;
т
H — слой осадков за холодный период (ноябрь — март) со средними
т
температурами ниже 0 °C, определяется по данным метеорологических
наблюдений, мм;
К — коэффициент, учитывающий объем стока талых вод в зависимости от
т
условий снеготаяния, определяется по данным нижеприведенной таблицы, для
которой зоны по условиям весеннего стока талых вод принимаются в
соответствии с рисунком 2 приложения 3 к настоящей Методике:
┌──────────────────────────────────┬────────┬─────────┬────────┬──────────┐
│ Зоны по условиям весеннего стока │ 1 │ 2 │ 3 │ 4 │
│ талых вод │ │ │ │ │
├──────────────────────────────────┼────────┼─────────┼────────┼──────────┤
│Значение коэффициента К │ 0,47 │ 0,56 │ 0,69 │ 0,77 │
│ т │ │ │ │ │
└──────────────────────────────────┴────────┴─────────┴────────┴──────────┘
К — коэффициент, учитывающий принимаемое к расчету размера вреда время
t
сброса вредных (загрязняющих) веществ по отношению к продолжительности
периода стока талых вод.
29. Коэффициенты К и К , определяемые по приложениям 2 и 3 для пунктов
q т
28.2 и 28.3 Методики, можно также получить на основании данных
справочников гидрометеорологической информации.
30. Исключен. — Приказ Минприроды России от 31.01.2014 N 47.
31. В приложении 4 к настоящей Методике даны примеры исчисления размера вреда, причиненного водным объектам вследствие нарушения водного законодательства.
2.2. Моль, молярная масса
2.2. Моль, молярная масса2.2. Моль, молярная масса
В химических процессах участвуют мельчайшие частицы – молекулы, атомы, ионы, электроны. Число таких частиц даже в малой порции вещества очень велико. Поэтому, чтобы избежать математических операций с большими числами, для характеристики количества вещества, участвующего в химической реакции, используется специальная единица – моль.
Моль — это такое количество вещества, в котором содержится определенное число частиц (молекул, атомов, ионов), равное постоянной Авогадро
Постоянная Авогадро NA определяется как число атомов, содержащееся в 12 г изотопа 12С:
Таким образом, 1 моль вещества содержит 6,02 • 1023 частиц этого вещества.
Исходя из этого, любое количество вещества можно выразить определенным числом молей ν (ню). Например, в образце вещества содержится 12,04 • 1023 молекул. Следовательно, количество вещества в этом образце составляет:
В общем виде:
где N – число частиц данного вещества;NA – число частиц, которое содержит 1 моль вещества (постоянная Авогадро).
Молярная масса вещества (M) – масса, которую имеет 1 моль данного вещества.
Эта величина, равная отношению массы m вещества к количеству вещества ν, имеет размерность кг/моль или г/моль. Молярная масса, выраженная в г/моль, численно равна относительной относительной молекулярной массе Mr (для веществ атомного строения – относительной атомной массе Ar).
Например, молярная масса метана CH4 определяется следующим образом:
M(CH4)=16 г/моль, т.
 е. 16 г CH4 содержат 6,02 • 1023 молекул.
е. 16 г CH4 содержат 6,02 • 1023 молекул.Молярную массу вещества можно вычислить, если известны его масса m и количество (число молей) ν, по формуле:
Соответственно, зная массу и молярную массу вещества, можно рассчитать число его молей: или найти массу вещества по числу молей и молярной массе: m = ν • MНеобходимо отметить, что значение молярной массы вещества определяется его качественным и количественным составом, т.е. зависит от Mr и Ar. Поэтому разные вещества при одинаковом количестве молей имеют различные массы m.
Пример
Вычислить массы метана CH4 и этана С2H6,
взятых в количестве ν = 2 моль каждого.
Молярная масса метана M(CH4) равна 16 г/моль;
молярная масса этана M(С2Н6) = 2 • 12+6=30 г/моль.
Отсюда: m(CH4) = 2 моль • 16 г/моль = 32 г;
m(С2Н6) = 2 моль • 30 г/моль = 60 г.

Таким образом, моль – это порция вещества, содержащая одно и то же число частиц, но имеющая разную массу для разных веществ, т.к. частицы вещества (атомы и молекулы) не одинаковы по массе.
n(CH4) = n(С2Н6), но m(CH4) (С2Н6)
Вычисление ν используется практически в каждой расчетной задаче.
Основные Химические формулы для решения задач.
| № | Количественные характеристики вещества | Обозначение | Единицы измерения | Формула для расчета |
|---|---|---|---|---|
| 1 | Плотность вещества | ρ | кг/м³ | ρ = m / V(Массу делим на объем вещества) |
| 2 | Относительная атомная масса элемента | Аr | — | Ar = ma / u см. в периодической система химических элементов |
| 3 | Атомная единица массы | u а.  е.м. е.м. | кг | u = 1/12 * ma (12C) const = 1.66*10-27 |
| 4 | Масса атома (абсолютная) | ma | кг | ma = Ar * u |
| 5 | Относительная молекулярная (формульная) масса вещества | Mr | — | Mr (AxBy)=m(AB) / u Mr(AxBy)=x*Ar(A) + y*Ar(B) |
| 6 | Масса молекулы (формульной единицы) | m M | кг | mM = Mr*u |
| 7 | Количество вещества | n | моль | n=m/M n=N/NA n=V/VM |
| 8 | Молярная масса (масса 1 моль вещества) | M | г/моль | M=m/n M=Mr M=Ar (для простых веществ) |
| 9 | Масса вещества | m | г (кг) | m=M*n m=ρ*V |
| 10 | Число структурных единиц | N | атомов, молекул, ионов, частиц, формульных единиц (Ф.Е.) | N=NA*n |
| 11 | Молярный объем — число 1 моль ГАЗООБРАЗНОГО вещества в нормальных условиях (н. у.) у.) | VM | л/моль | const=22,4 |
| 12 | Объем газа при н.у. | V | л | V=VM*n V=m/ρ |
| 13 | Постоянная Авогадро | NA | частиц/моль | const=6,02*1023 |
| 14 | Массовая доля вещества (омега) | ωЭ/В | % | ωЭ/В = (Ar(э) * k) / Mr(В) |
| Формула | Название кислоты | Формула кислотного остатка | Название кислотного остатка |
|---|---|---|---|
| HF | Фтороводород, плавиковая | F— | Фторид |
| HCl | Хлороводород, соляная | Cl— | Хлорид |
| HBr | Бромоводород | Br— | Бромид |
| HI | Йодоводород | I— | Йодид |
| h3S | Сероводород | S2- | Сульфид |
| HCN | Циановодородная | CN— | Цианид |
| HNO2 | Азотистая | NO2— | Нитрит |
| HNO3 | Азотная | NO3— | Нитрат |
| h4PO4 | Ортофосфорная | PO43- | Фосфат |
| h4AsO4 | Мышьяковая | AsO43- | Арсенат |
| h3SO3 | Сернистая | SO32- | Сульфит |
| h3SO4 | Серная | SO42- | Сульфат |
| h3CO3 | Угольная | CO32- | Карбонат |
| h3SiO3 | Кремниевая | SiO32- | Силикат |
| h3CrO4 | Хромовая | CrO42- | Хромат |
| h3Cr2O7 | Дихромовая | Cr2O72- | Дихромат |
| HMnO4 | Марганцовая | MnO4— | Перманганат |
| HClO | Хлорноватистая | ClO— | Гипохлорит |
| HClO2 | Хлористая | ClO2— | Хлорит |
| HClO3 | Хлорноватая | ClO3— | Хлорат |
| HClO4 | Хлорная | ClO4— | Перхлорат |
| HCOOH | Метановая, муравьиная | HCOO— | Формиат |
| Ch4COOH | Этановая, уксусная | Ch4COO— | Ацетат |
| h4C2O4 | Этандиовая, щавелевая | C2O42- | Оксалат |
Нажмите на картинку для увеличения
Формула 1.
 Масса выиграл квалификацию в Испании :: Формула-1 :: РБК Спорт
Масса выиграл квалификацию в Испании :: Формула-1 :: РБК СпортВ Валенсии на Гран-При Испании бразилец Фелипе Масса выиграл квалификацию в гонках класса «Формула 1» и в воскресенье стартует в гонке с поул-позишн.
Читайте нас в
Новости НовостиВ Валенсии на Гран-При Испании бразилец Фелипе Масса выиграл квалификацию в гонках класса «Формула 1» и в воскресенье стартует в гонке с поул-позишн.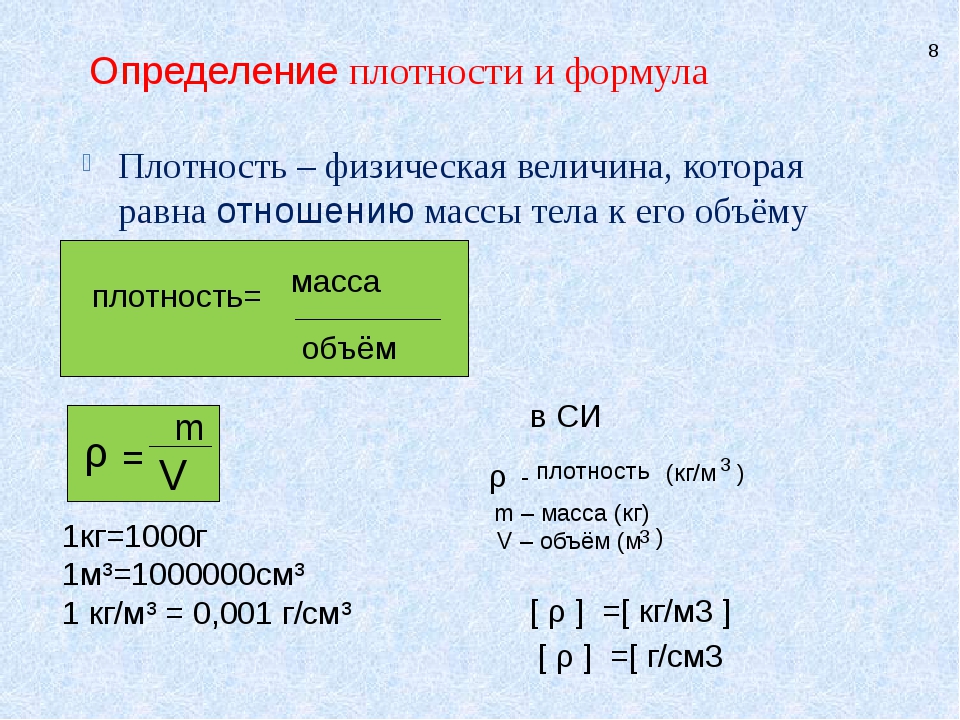
Формула 1. Гран-При Испании. Квалификация
1. Масса (Бразилия, «Феррари») — 1.38,989
2. Хэмилтон (Великобритания, «Макларен») — 1.39,199
3. Кубица (Польша, «БМВ-Заубер») — 1.39,392
4. Райкконен (Финляндия, «Феррари») — 1.39,488
5. Ковалайнен (Финляндия, «Макларен») — 1.39,937
6. Феттель (Германия, «Торо Россо») — 1.40,142
7. Трулли (Италия, «Тойота») — 1.40,309
8. Хайдфельд (Германия, «БМВ-Заубер») — 1.40,361
9. Росберг (Германия, «Уильямс») — 1.40,721
10. Бурдэ (Франция, «Торо Россо») — 1.40,750
11. Накаджима (Япония, «Уильямс») — 1.38,428
12. Алонсо (Испания, «Рено») — 1.38,435
13. Глок (Германия, «Тойота») — 1.38,499
14. Уэббер (Австралия, «Ред Булл») — 1.38,515
15. Пике (Бразилия, «Рено») — 1.38,744
16. Баттон (Великобритания, «Хонда») — 1.38,880
17. Култхард (Шотландия, «Ред Булл») — 1.39,235
18. Физикелла (Италия, «Форс Индия») — 1.39,268
19. Баррикелло (Бразилия, «Хонда») — 1.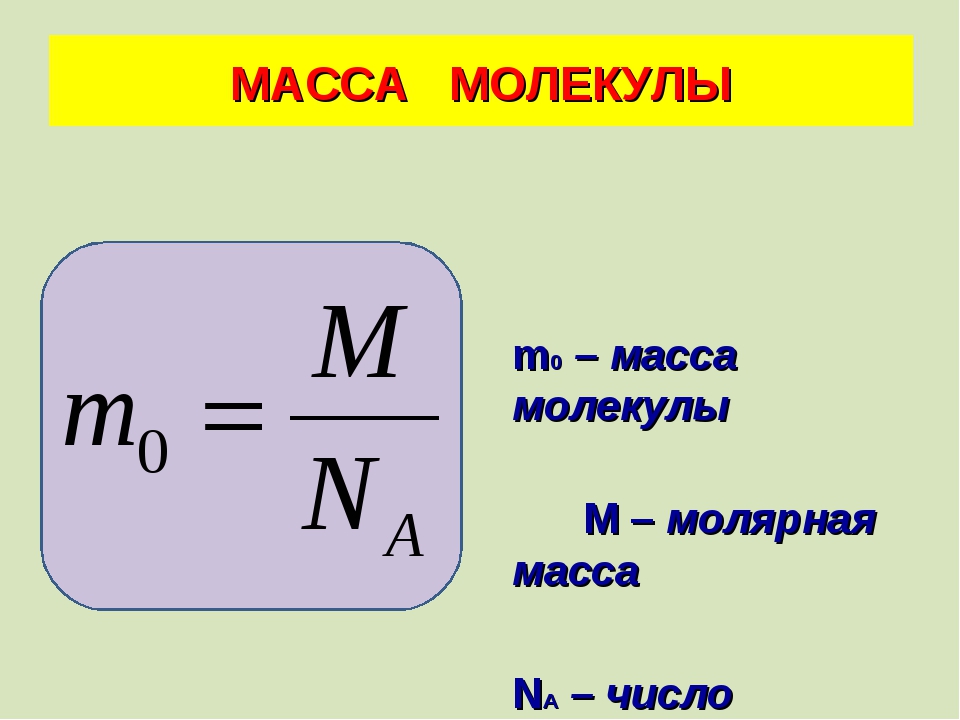 39,811
39,811
20. Сьютиль (Германия, «Форс Индия») — 1.39,943
Фелипе Масса выигрывает Гран-при Европы — ДРАЙВ
Говорим Гран-при Европы — подразумеваем Нюрбургринг, принимавший этап Формулы-1 девять последних лет. Только не в этот раз: теперь Гран-при Европы проводится в испанской Валенсии. Работа по подготовке великолепной городской трассы заслуживает уважения. Перед стартом трудно было подумать, что по ходу гонки не раз вспомнится Нюрбургринг — там было интереснее!
Нас уже избаловали: даже традиционно скучные гонки, например в Венгрии, в этом сезоне оборачиваются незабываемым шоу. Поэтому от заездов по незнакомой для пилотов трассе, да ещё по городу, мы искренне ждали сенсаций. А вышло совсем не так.
Роберт Кубица может быть доволен своим третьим местом — поляк стал ещё ближе к Райкконену в личном зачёте. Но BMW всё больше отстаёт от Ferrari и Mclaren в командном.
Но BMW всё больше отстаёт от Ferrari и Mclaren в командном.
Борьбы на трассе практически не было. Все три лидера квалификации — на подиуме. Масса безукоризненно стартовал с поул-позиции и сразу ушёл в отрыв. Видимо, в Фелипе было столько спортивной злости от неудачи в прошлой гонке, что в Валенсии он не дал соперникам ни единого шанса. Он как бы вернул себе то, что насмешница-судьба отняла у него три недели назад в Будапеште.
Фернандо Алонсо на домашнем гран-при не повезло: его гонка закончилась уже на первом круге из-за столкновения с Кадзуки Накадзимой.
Старт лидера чемпионата Льюиса Хамильтона был под вопросом из-за болей в шее. Но британец провёл стабильную гонку, заняв второе место и заработав такие важные восемь очков. Однако навязать Массе борьбу не удалось — Макларену банально не хватило скорости.
Представители Ferrari после гонки прокомментировали сход Райкконена: говорят, двигатель сгорел по той же причине что и три недели назад на болиде Фелипе Массы.
А вот Райкконен провел одну из худших гонок в карьере. Кими — гонщик, не склонный к ошибкам. Но в этот раз он неудачно стартовал и по ходу гонки выглядел довольно блёкло. На втором пит-стопе финн допустил серьёзный промах, стоивший ему лишних секунд — рванул с места раньше времени, сбив механика. Последнего отправили в медицинский центр. А на следующем круге умер мотор Ferrari, лишив Райкконена надежды заработать хоть какие-то очки.
Трасса в Валенсии красива и интересна, но о прошедшей здесь гонке этого не скажешь.
Гонок в сезоне остаётся всё меньше, а Кими продолжает хандрить. Не исключено, что именно потерянных в Валенсии очков ему не хватит в конце чемпионата. Как тут снова не вспомнить Нюрбургринг: на Гран-при Европы в 2005-м за круг до финиша на машине Райкконена вырвало переднюю подвеску, и он упустил победу, стоившую ему в итоге титула.
Шестое место для Toro Rosso — страшно подумать, что будет, если в распоряжении Феттеля окажется действительно быстрая машина. Кстати, за ним — лучшее время по ходу второй части квалификации!
Кстати, за ним — лучшее время по ходу второй части квалификации!
| Результаты Гран-при Европы — 2008 | ||||
|---|---|---|---|---|
| Позиция | Пилот | Команда | Время | Количество пит-стопов |
| 1 | Фелипе Масса | Ferrari | 1:35:32.339 | 2 |
| 2 | Льюис Хамильтон | McLaren Mercedes | + 5.611 | 2 |
| 3 | Роберт Кубица | BMW Sauber | + 37.353 | 2 |
| 4 | Хейкки Ковалайнен | McLaren Mercedes | + 39.703 | 2 |
| 5 | Ярно Трулли | Toyota | + 50.684 | 2 |
| 6 | Себастьян Феттель | Toro Rosso — Ferrari | + 52. 625 625 |
2 |
| 7 | Тимо Глок | Toyota | + 1:07.990 | 1 |
| 8 | Нико Росберг | Williams — Toyota | + 1:11.457 | 2 |
| 9 | Ник Хайдфельд | BMW Sauber | + 1:22.177 | 2 |
| 10 | Себастьен Бурдэ | Toro Rosso — Ferrari | + 1:29.794 | 2 |
| 11 | Нельсон Пике | Renault | + 1:32.717 | 1 |
| 12 | Марк Уэббер | Red Bull — Renault | + 1 круг | 1 |
| 13 | Дженсон Баттон | Honda | + 1 круг | 1 |
| 14 | Джанкарло Физикелла | Force India — Ferrari | + 1 круг | 1 |
| 15 | Кадзуки Накадзима | Williams — Toyota | + 1 круг | 2 |
| 16 | Рубенс Баррикелло | Honda | + 1 круг | 1 |
| 17 | Дэвид Култхард | Red Bull — Renault | + 1 круг | 2 |
Лучший круг: Фелипе Масса (Ferrari) — 1:38. 708 (36 круг, 197.637 км/ч) 708 (36 круг, 197.637 км/ч) |
||||
| Причины сходов | |||
|---|---|---|---|
| Пилот | Команда | Круг | Причина |
| Кими Райкконен | Ferrari | 46 | Мотор |
| Адриан Сутиль | Force India — Ferrari | 42 | Авария |
| Фернандо Алонсо | Renault | 1 | Авария |
| Положение в чемпионате: личный зачёт | |||
|---|---|---|---|
| Позиция | Пилот | Команда | Очки |
| 1 | Л. Хамильтон | McLaren Mercedes | 70 |
| 2 | Ф. Масса | Ferrari | 64 |
| 3 | К. Райкконен | Ferrari | 57 |
| 4 | Р.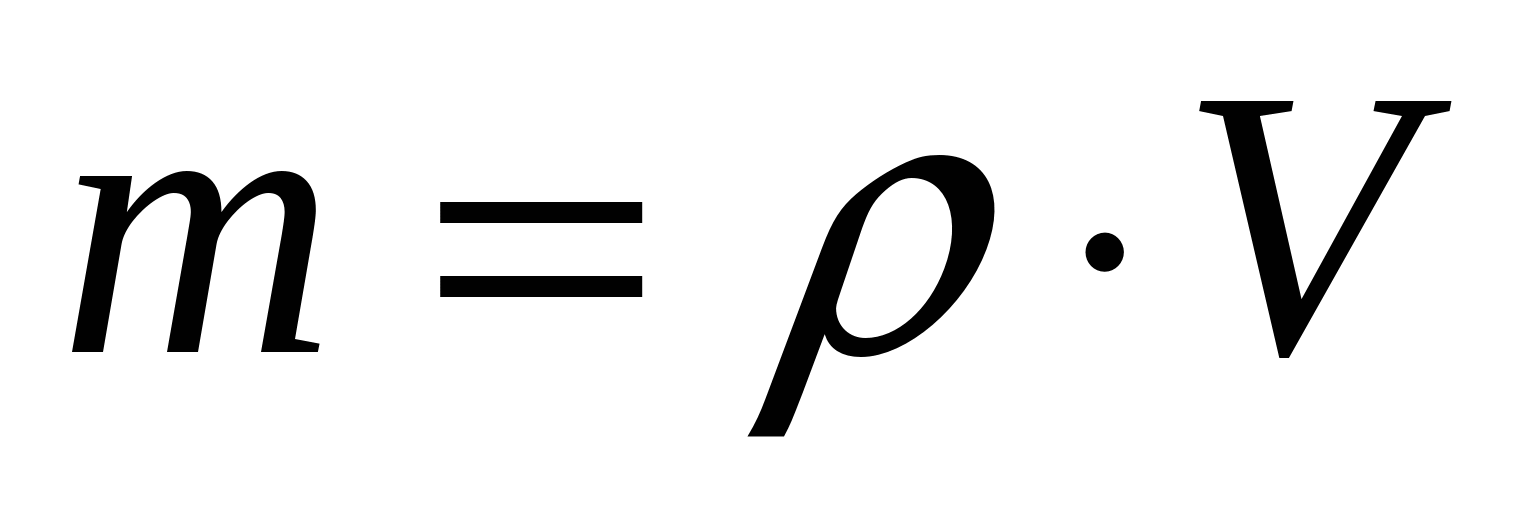 Кубица Кубица |
BMW Sauber | 55 |
| 5 | Х. Ковалайнен | McLaren Mercedes | 43 |
| 6 | Н. Хайдфельд | BMW Sauber | 41 |
| 7 | Я. Трулли | Toyota | 26 |
| 8 | М. Уэббер | Red Bull — Renault | 18 |
| 9 | Ф. Алонсо | Renault | 18 |
| 10 | Т. Глок | Toyota | 15 |
| 11 | Н. Пике | Renault | 13 |
| 12 | Р. Баррикелло | Honda | 11 |
| 13 | Н. Росберг | Williams — Toyota | 9 |
| 14 | С. Феттель | Toro Rosso — Ferrari | 9 |
| 15 | К. Накадзима Накадзима |
Williams — Toyota | 8 |
| 16 | Д. Култхард | Red Bull — Renault | 6 |
| 17 | Д. Баттон | Honda | 3 |
| 18 | С. Бурдэ | Toro Rosso — Ferrari | 2 |
| Положение в чемпионате: Кубок конструкторов | |||
|---|---|---|---|
| Позиция | Команда | Мотор | Очки |
| 1 | Ferrari | Ferrari | 121 |
| 2 | McLaren Mercedes | Mercedes | 113 |
| 3 | BMW Sauber | BMW | 96 |
| 4 | Toyota | Toyota | 41 |
| 6 | Renault | Renault | 31 |
| 5 | Red Bull | Renault | 24 |
| 7 | Williams | Toyota | 17 |
| 8 | Honda | Honda | 14 |
| 9 | Scuderia Toro Rosso | Ferrari | 11 |
Что такое масса? — Определение, единицы, формула и примеры
Массу лучше всего понимать как количество материи, присутствующей в любом объекте или теле.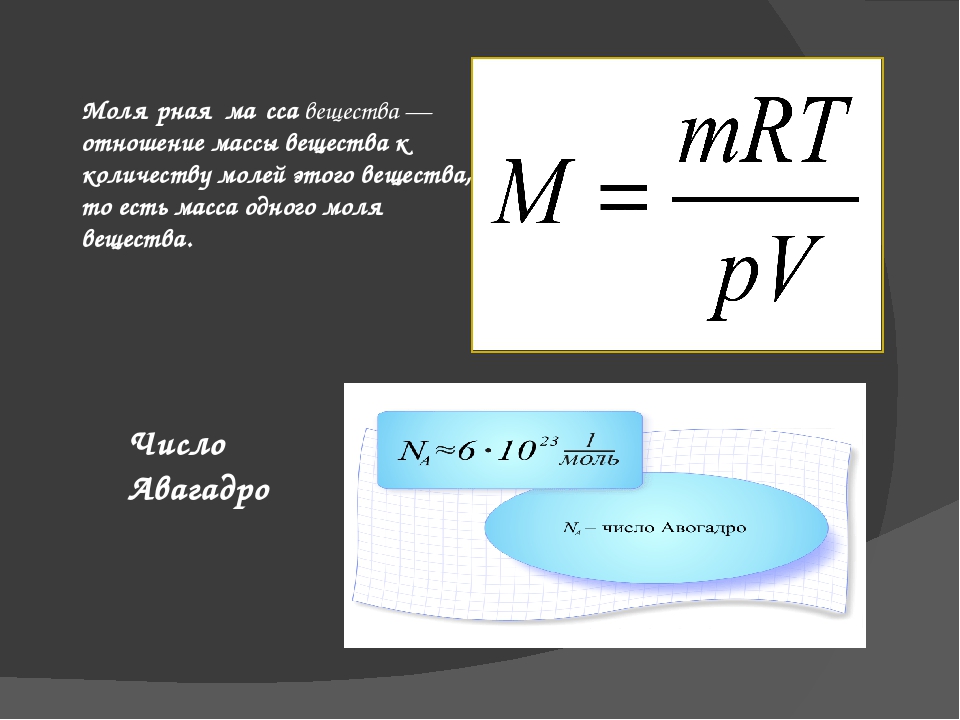 Все, что мы видим вокруг себя, имеет массу. Например, стол, стул, ваша кровать, футбольный мяч, стакан и даже воздух имеют массу. При этом все объекты легкие или тяжелые из-за своей массы. На этом уроке мы узнаем, что такое масса, как ее вычислить, и ее примеры, открывая при этом интересные факты о ней.
Все, что мы видим вокруг себя, имеет массу. Например, стол, стул, ваша кровать, футбольный мяч, стакан и даже воздух имеют массу. При этом все объекты легкие или тяжелые из-за своей массы. На этом уроке мы узнаем, что такое масса, как ее вычислить, и ее примеры, открывая при этом интересные факты о ней.
Что такое масса?
В физике масса является самым основным свойством материи и одной из фундаментальных величин. Масса определяется как количество вещества, присутствующего в теле. Единицей массы в системе СИ является килограмм (кг). Формулу массы можно записать так:
Примечание : масса тела постоянна; он не меняется в любое время. Только в определенных крайних случаях, когда от тела отдается или отнимается огромное количество энергии, масса может воздействовать.Например, при ядерной реакции крошечное количество вещества превращается в огромное количество энергии, это уменьшает массу вещества.
Что такое единица массы?
Существуют различные единицы измерения массы, такие как килограммы, граммы, фунты, фунты и т. д., но единицей измерения массы в системе СИ является «килограмм» или кг. Каждая единица массы может быть преобразована в другие единицы с помощью соответствующей формулы преобразования, не затрагивающей смысла и сути измеряемой величины.
д., но единицей измерения массы в системе СИ является «килограмм» или кг. Каждая единица массы может быть преобразована в другие единицы с помощью соответствующей формулы преобразования, не затрагивающей смысла и сути измеряемой величины.
Примечание. 1 кг равен 2,20462 фунта.
Разница между массой и весом
Люди часто путают массу и вес и в конечном итоге используют эти два термина как синонимы. Однако масса и вес — это два разных термина, и важно понимать разницу между ними. Разница между массой и весом показана в приведенной ниже таблице.
| Масса | Вес | |
|---|---|---|
| Определение | Масса определяется как количество вещества в веществе | Вес определяется как количество силы, действующей на массу объекта из-за ускорения под действием силы тяжести. |
| Обозначение | Масса представлена буквой «М». | Масса представлена буквой «W». |
| Формула | •Масса тела всегда постоянна. • Один из способов расчета массы: масса = объем × плотность. | •Вес является мерой гравитационной силы, действующей на массу. • Формула веса: Вес = масса × ускорение свободного падения |
| Единица измерения | Единицей массы в СИ является «килограмм». | Единицей веса в системе СИ является Ньютон (Н). |
| Количество Тип | •Масса является базовой величиной. • Масса имеет только величину и, следовательно, это скалярная величина | . •Вес является производной величиной. • Вес имеет как величину, так и направление (к центру тяжести) и, следовательно, является векторной величиной. |
| Измерительный прибор | Массу можно легко измерить с помощью любых обычных весов. Например, балочный баланс, рычажный баланс, панорамный баланс и т. д. | Вес можно измерить с помощью пружинных весов или по приведенной выше формуле. |
Знаете ли вы, что у нас разный вес на Земле, на Луне и в космосе? Однако наша масса везде одинакова.
Теперь давайте посмотрим на некоторые важные факты, связанные с массой:
- Масса имеет только величину, следовательно, это скалярная величина.
- Вес имеет как величину, так и направление; это векторная величина.
- Массу также можно определить как «энергию, запасенную в частицах».
- Масса представляет собой общее количество атомов или частиц, которые оно содержит.
Пример 1: Сэм на Земле весит 1000 фунтов. На какой-нибудь другой планете вес Сэма составил бы 38 % от земного. Сколько бы Сэм весил на этой планете?
Решение: Мы знаем, что вес Сэма на Земле составляет 1000 фунтов, а его вес на другой планете будет составлять 38 % от земного. Следовательно, вес Сэма на другой планете = 38 % × его вес на Земле = 0,38 × 1000 фунтов = 380 фунтов 90 003.
Следовательно, вес Сэма на другой планете = 38 % × его вес на Земле = 0,38 × 1000 фунтов = 380 фунтов 90 003.Пример 2: Масса объекта составляет 6000 фунтов. Вычислите его массу в тоннах.
Решение: Мы знаем, что 1 тонна = 2000 фунтов. Таким образом, 6000 фунтов = 6000/2000=3 тонны.Пример 3: У Дамиана есть книга массой 2,2 кг. Каков вес книги на Земле?
Решение:
Масса учебника = 2.2\)
Вес учебника = 21,56 Н
Следовательно, вес учебника на Земле равен 21,56 Н.
перейти к слайду
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами
Забронируйте бесплатный пробный урок
Часто задаваемые вопросы по Mass
Имеет ли воздух массу?
Да, воздух имеет массу. Например, надутый воздушный шар весит тяжелее, чем сдутый воздушный шар, что доказывает, что воздух внутри надутого воздушного шара имеет массу.
Например, надутый воздушный шар весит тяжелее, чем сдутый воздушный шар, что доказывает, что воздух внутри надутого воздушного шара имеет массу.
Масса и объем одинаковы?
Масса – это количество материи, из которой состоит объект. Объем — это количество свободного места, которое занимает объект. Следовательно, масса и объем не совпадают.
Плотность и масса — одно и то же?
Масса измеряет количество вещества, присутствующего в веществе. Плотность показывает количество вещества в данном пространстве для вещества.Плотность и масса могут быть такими же, как единица объема.
Вес и масса — одно и то же?
Нет, вес и масса не одно и то же. Вес – это сила, действующая на тело, а масса – это количество вещества в теле. Вес может изменяться в зависимости от силы, в то время как масса постоянна.
Что такое единица массы в СИ?
Единицей массы в системе СИ являются килограммы (кг).
Что такое формула массы?
Формула, используемая для расчета массы объекта: Плотность × Объем.
Какая формула массы?
Масса — это свойство физических объектов и мера устойчивости тела к ускорению. Можно рассматривать массу объекта как меру того, сколько физического «вещества» составляет этот объект.
В отличие от реляционных свойств, таких как положение, скорость или потенциальная энергия, которые всегда должны определяться по отношению к другому объекту или контрольной точке, масса является внутренним свойством, которым объект обладает независимо от его отношения к другим вещам.Массу объекта можно рассчитать несколькими способами:
- масса=плотность×объем (m=ρV) . Плотность — это мера массы на единицу объема, поэтому массу объекта можно определить, умножив плотность на объем.
- масса=сила÷ускорение (m=F/a) . Согласно второму закону Ньютона (F=ma), ускорение тела прямо пропорционально приложенной к нему силе. Следовательно, величина ускорения, сопровождающего приложение постоянной силы, обратно пропорциональна массе.

- масса=вес÷ускорение свободного падения (m=Вт/г). Вес – это произведение ускорения массы в гравитационном поле. В зависимости от силы гравитационного ускорения вес будет разным.
Все эти три формулы являются способом определения массы объекта. Поскольку масса является фундаментальным свойством, она не определяется в терминах других единиц, как джоуль (Дж) Ньютона (Н). Существуют и другие способы расчета массы объекта, но эти три формулы являются наиболее распространенными.
м=ρV
м=Вт/г
м=F/a
Единицы массы
СИ-принятая единица массы
Килограмм является единственной базовой единицей СИ с приставкой в названии (кило-). Первоначально один килограмм определялся как масса одного кубического децилитра (дл) воды при температуре ее плавления. С 1889 года килограмм был переопределен как масса Международного прототипа килограмма (IPK), физического артефакта, предназначенного для универсальной эталонной массы килограмма.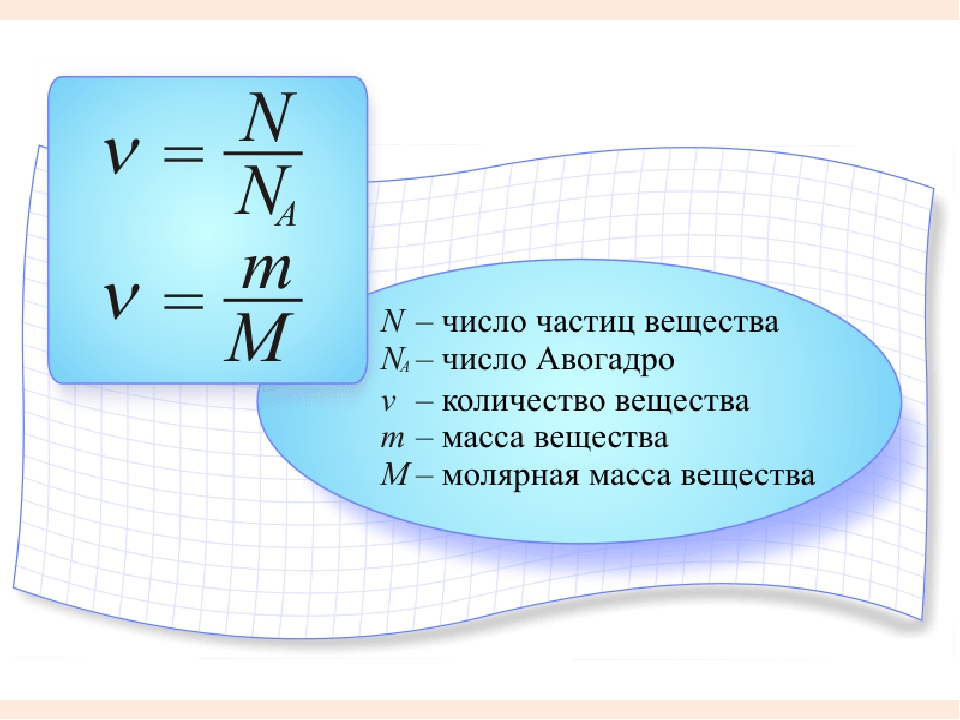 Первоначально ИПК представлял собой чугунную гирю. В настоящее время принятым ИПК является цилиндр высотой 39 мм, изготовленный из специального платинового сплава.
Первоначально ИПК представлял собой чугунную гирю. В настоящее время принятым ИПК является цилиндр высотой 39 мм, изготовленный из специального платинового сплава.
«Слова тоже имеют подлинную субстанцию — массу, вес и удельный вес». — Тим О’Брайен
По состоянию на 2018 год килограмм является единственной единицей СИ, для которой в качестве эталонного значения используется физический объект. Все остальные единицы СИ были переопределены с точки зрения фундаментальных физических констант, таких как скорость света или постоянная Планка.В ноябре 2018 года Генеральная конференция мер и весов (GCPM) проголосовала за новое определение килограмма с точки зрения фундаментальных физических констант, и это изменение вступит в силу 20 мая 2019 года.
Плотность объекта, иногда обозначаемая греческой буквой «ρ», является мерой массы на единицу объема. По сути, плотность говорит вам, насколько плотно упакована масса объекта. Чем плотнее объект, тем больше его масса на единицу объема.
Например, вода имеет плотность 977 кг/м 3 при стандартной температуре и давлении. То есть один кубический метр воды имеет массу 977 кг. Если мы знаем плотность и объем вещества, мы также можем вычислить массу этого вещества. Допустим, у нас есть 0,7 м 3 пробы воды. Какова масса этого образца?
Решение для массы дает нам:
m=ρV
m=(0,7 м 3 )(977 кг/м 3 ) = 683 кг
0.5 кубометров воды при стандартной температуре и давлении будут иметь массу 683 кг.
Некоторые объекты невероятно плотные. Нейтронная звезда, например, имеет среднюю плотность 1,1 x 10 90 152 18 90 153 кг/м 90 152 3 90 153 . Одна чайная ложка нейтронной звезды на Земле весила бы около 100 миллионов тонн.
«Масса становится неподвижной; он не может маневрировать и, следовательно, не может одерживать победы, он может только сокрушать своим весом». — Ганс фон Сект
From Force And Acceleration
Свойство массы понимается также как мера сопротивления физического объекта ускорению под действием внешней силы. Это понятие массы иногда называют инерционной массой . Инерция — это тенденция движущегося тела продолжать находиться в постоянном состоянии движения, поэтому инерционная масса — это мера того, насколько сильно инерционно обладает тело и насколько трудно изменить состояние своего движения. Связь между массой, силой и ускорением выражается вторым законом Ньютона F=ma. Это математическое соотношение говорит нам о том, что перед лицом постоянной силы более массивное тело будет ускоряться медленнее.Измеряя силу, приложенную к телу, и измеряя наблюдаемое ускорение, мы можем вычислить массу тела.
Это понятие массы иногда называют инерционной массой . Инерция — это тенденция движущегося тела продолжать находиться в постоянном состоянии движения, поэтому инерционная масса — это мера того, насколько сильно инерционно обладает тело и насколько трудно изменить состояние своего движения. Связь между массой, силой и ускорением выражается вторым законом Ньютона F=ma. Это математическое соотношение говорит нам о том, что перед лицом постоянной силы более массивное тело будет ускоряться медленнее.Измеряя силу, приложенную к телу, и измеряя наблюдаемое ускорение, мы можем вычислить массу тела.
Например, мы прикладываем силу 748 Н к металлическому кубу и измеряем его ускорение как 21 м/с 2 . Какова масса металлического куба? Мы можем рассчитать массу, разделив величину силы на величину ускорения так:
м=F/a
м=(748 Н)/(21 м/с 2 ) ≈ 35,62 кг
Итак, мы знаем, что металлический куб должен иметь массу 35.62 кг.
From Weight
Строго говоря, вес и масса — разные вещи. В английском языке два слова «вес» и «масса» являются синонимами, однако в физических науках они имеют разные значения. Масса — это неизменное свойство, которое не меняется от места к месту. Вес является мерой силы гравитационного поля, действующего на массивное тело. Поскольку напряженность гравитационного поля может различаться, т. Е. Луна имеет более слабую напряженность гравитационного поля, чем Земля, вес объекта может различаться в разных средах.
Соотношение между массой и весом выражается формулой W = mg, где g — мера ускорения свободного падения. Точное значение g зависит от местоположения. На Земле g имеет значение приблизительно 9,81 м/с 2 , а на Луне g составляет около 1,6 м/с 2 . Выражение W=mg дает вес в ньютонах, в то время как повседневное понимание веса дается в фунтах (lbs) коэффициент преобразования из ньютонов в фунты составляет около 1 N=0,22 фунта.
Например, на поверхности Земли где г=9. 81 м/с 2 , 50-килограммовый объект будет иметь вес в фунтах:
81 м/с 2 , 50-килограммовый объект будет иметь вес в фунтах:
W=(50кг)(9,81м/с 2 )=490,5Н
Преобразование ньютонов в фунты дает нам:
490,5 Н(0,22 фунта/1 Н)≈ 108 фунтов
И наоборот, на Луне, где g имеет значение 1,6 м/с 2 , объект массой 50 кг будет весить:
W=50(кг)( 1,6 м/с 2 )(0,22 фунта/1 Н) ≈ 18 фунтов
Тот же 50-килограммовый объект весит 108 фунтов на Земле и 18 фунтов на Луне.
Точно так же, если мы знаем вес объекта, мы можем работать в обратном направлении, чтобы вычислить его массу. Скажем, объект весит 160 фунтов Земли. мы можем рассчитать массу объекта следующим образом: 2 )≈ 83,4 кг
Итак, 180-фунтовое тело на Земле имеет массу около 84,3 кг.
Массово-энергетическая эквивалентность
Очень долгое время ученые считали, что массу объекта можно считать полностью независимой от других его свойств.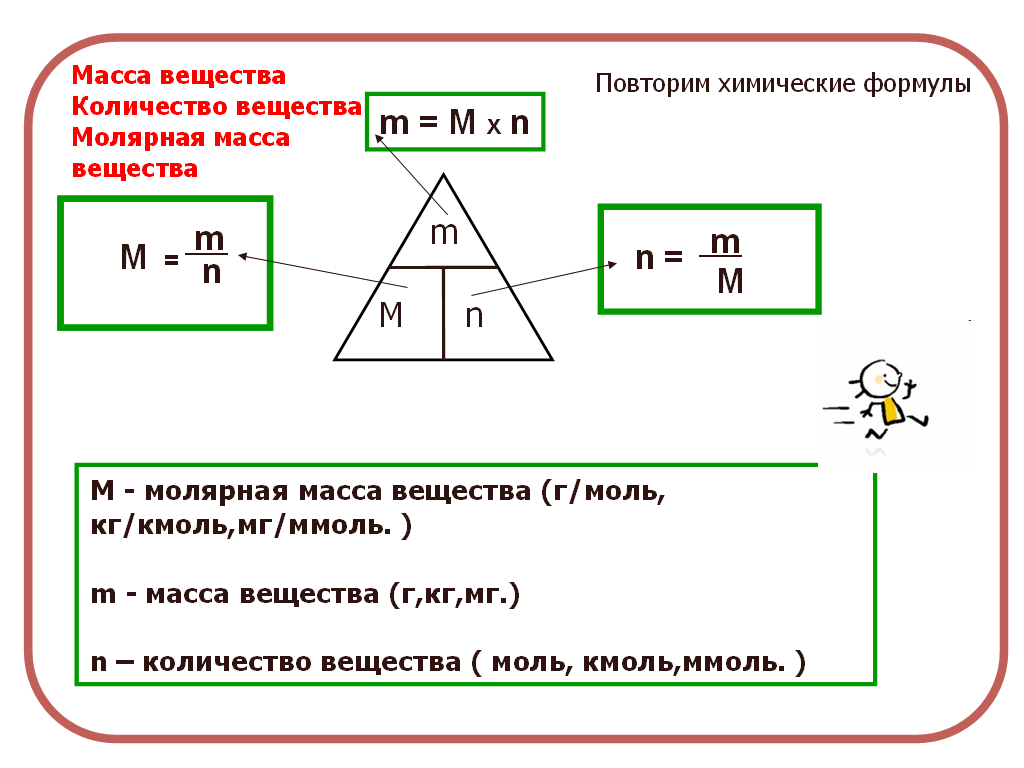 Однако в начале 20 века специальная теория относительности Эйнштейна показала, что масса и энергия на самом деле являются двумя разными названиями одной и той же физической величины. В частности, масса объекта и его полная энергия связаны знаменитым уравнением Эйнштейна E=mc 2 , где c — скорость света в вакууме.
Однако в начале 20 века специальная теория относительности Эйнштейна показала, что масса и энергия на самом деле являются двумя разными названиями одной и той же физической величины. В частности, масса объекта и его полная энергия связаны знаменитым уравнением Эйнштейна E=mc 2 , где c — скорость света в вакууме.
E=mc 2 говорит нам, что полная энергия неподвижного тела прямо пропорциональна его массе с коэффициентом c 2 . Поскольку c=3 000 000 м/с, c 2 является чрезвычайно большим фактором.Следовательно, даже крошечный кусочек массы содержит подавляющее количество внутренней энергии. Для сравнения, общее количество энергии от полного преобразования 1 грамма вещества в энергию примерно равно 21,5 килотоннам тротила — мощности атомной бомбы, сброшенной на Хиросиму.
«Любой дурак может знать. Суть в том, чтобы понять». — Альберт Эйнштейн
В некоторых физических процессах, таких как деление ядер или движение тела в интенсивном гравитационном поле, материя преобразуется в энергию и высвобождается в виде большого количества света и тепла. В частности, уравнение Эйнштейна говорит нам, как мы можем рассчитать количество энергии, высвобождаемой во время таких реакций.
В частности, уравнение Эйнштейна говорит нам, как мы можем рассчитать количество энергии, высвобождаемой во время таких реакций.
Скажем, 30 кг урана (Ur) помещают в ядерный реактор. При делении примерно 0,1% этой массы полностью превращается в энергию. Сколько энергии получается?
0,1% от 30 кг это 0,3 кг. Подключение этого в уравнение Эйнштейна дает нам:
E = (0,3 кг) (3 000 000) 2 = (0.3) (8.98755179 × 10 2 3) = 2.69626554 × 10 16 J Полностью преобразование всего 0 .3 кг (0,6 фунта) вещества в энергию выделяет 2,69626554 × 10 16 Дж энергии. Это количество примерно равно взрыву более 6 миллионов тонн тротила (12 миллиардов фунтов), что достаточно, чтобы полностью сровнять с землей даже самые крупные города. Мы также можем работать в обратном направлении от некоторого количества энергии, чтобы определить количество преобразованной массы. Скажем, какая-то реакция деления высвобождает 1,6178 × 10 16 джоулей энергии. 1.6178 × 10 16 J = M (8 J = M (8 179 × 10 16 ) (1.6178 × 10 16 ) / 8.987555179 × 10 16 ) = M m ≈ 0,18 кг Так примерно 0,18 кг масса превратилась в энергию. Только недавно ученые начали открывать ответ на вопрос, почему частицы вообще имеют массу. В 1960-х годах несколько ученых заметили некоторые проблемы с их уравнениями, описывающими поведение элементарных частиц.В частности, их уравнения предсказывали, что некоторые частицы, генерируемые во время высокоскоростных столкновений, не будут иметь массы. Однако экспериментальное наблюдение показало, что эти частицы действительно имели ненулевую массу. Ученые предположили, что масса бозона может генерироваться взаимодействием между этими бозонами и всепроникающим полем, называемым полем Хиггса (в честь одного из его теоретиков Питера Хиггса). Была ли эта статья полезной? Существует два способа определения массы объекта. Инерционная масса определяется как сопротивление объекта ускорению. Это означает, что чем больше инерционная масса, тем труднее ускорить этот объект.Давайте снова посмотрим на наш шар для боулинга и мяч для пинг-понга. Если я приложу к обоим шарикам одинаковую силу, ускорение какого тела будет больше? Ответ — шарик для пинг-понга, потому что он имеет меньшую инерционную массу и, следовательно, мяч для пинг-понга будет легче разогнать, чем шар для боулинга. Суммарная сила объекта равна произведению массы на ускорение.Массу можно рассчитать, разделив результирующую силу, действующую на объект, на ускорение объекта. Говоря о чистой силе, мы используем единицы килограмм-метр в секунду в квадрате. Это также известно как Ньютон. Единицы ускорения — метры на секунды в квадрате, а единицы массы — килограммы. Давайте сделаем пример. Вы даете магазинной тележке толчок в 8,0 ньютонов, заставляя ее ускоряться со скоростью 0,50 метра в секунду в секунду.Какова масса тележки для покупок? Мы знаем, что масса равна чистой силе, деленной на ускорение. Мы знаем, что чистое число силы равно 8 ньютонам, или 8 килограммам в секунду в квадрате. Для большинства объектов вам не нужно знать силу или ускорение, если у вас есть шкала. Второй метод, используемый для определения массы объекта, состоит в том, чтобы просто положить объект на весы. Если весы имеют единицы измерения граммы или килограммы, они измеряют массу. Любые весы с единицами измерения в фунтах измеряют вес, который, как мы теперь знаем, является совершенно другим измерением. Конечно, для некоторых объектов, таких как корабль или автомобиль, очень сложно найти масштаб для таких массивных объектов.Затем в этих случаях вы можете планировать эксперименты, в которых вы прикладываете известную силу к объекту, а затем измеряете результирующее ускорение. Масса — это мера того, сколько вещества содержится в объекте. Более формально, масса или инерционная масса является мерой сопротивления ускорению. Чем больше инерционная масса, тем сложнее разогнать объект. Мы можем либо измерить массу с помощью весов, либо вычислить массу объекта.Однако, чтобы рассчитать массу объекта, нам нужно знать силу, действующую на объект, и результирующее ускорение. Выберите расчет плотности p, массы m или объема V. Введите два других значения, и калькулятор вычислит третье значение в выбранных единицах измерения. Вы также можете ввести экспоненциальное представление, такое как 3.45e22. \( p = \dfrac{m}{V} \) Где: Калькулятор плотности использует формулу p=m/V, или плотность (p) равна массе (m), деленной на объем (V). Для значения 165778 при выборе 4 значащих цифр будет возвращено 165800. Для значения 0,00165778 при выборе 4 значащих цифр будет возвращено 0,001658. См. также наши справочные заметки по
значимые фигуры. Решая плотность, массу или объем, мы можем использовать следующие формулы: Рассчитать p Учитывая m и V \( p = \dfrac{m}{V} \) Вычислить m Учитывая p и V \( м = пВ \) Рассчитать V по данным p и m \(V = \dfrac{m}{p} \) Кубический корень объема помогает в мысленной визуализации фактического объема. Еще раз спасибо пользователю, который предложил этот калькулятор! \(\sqrt[3]{V} \) Механика твердого тела сохранение массы является фундаментальной концепцией
физика наряду с сохранением
энергии и закон сохранения импульса.В некоторой проблемной области количество массы остается постоянным — масса
не создается и не уничтожается. Это кажется совершенно очевидным, пока
поскольку речь не идет о черных дырах или очень экзотической физике
проблемы. Массу любого объекта можно определить, умножив
объем
объекта плотностью
объект. Когда мы перемещаем твердый объект, как показано в верхней части
при скольжении предмет сохраняет свою форму, плотность и объем. Масса
поэтому объект остается константой между состоянием «а» и состоянием
«б. Гидростатика В центре рисунка считаем количество статичных жидкость ,
жидкость или газ.
Если мы изменим жидкость из некоторого состояния «а»
в другое состояние «b» и позволяем ему остановиться, мы находим, что
в отличие от твердого тела, жидкость может менять свою форму. Количество жидкости,
однако остается прежним. Мы
можно рассчитать количество жидкости, умножив плотность
раза больше объема. Поскольку масса остается постоянной, произведение
плотность и объем также остаются постоянными.(Если плотность остается
постоянным, объем также остается постоянным.) Форма может меняться,
но масса остается прежней. Гидродинамика Наконец, внизу слайда мы рассматриваем изменения для
жидкость, которая движется через нашу область. Нет накопления или
истощение массы, поэтому масса сохраняется в домене. Поскольку
жидкость движется, определение количества массы становится немного сложным.
Рассмотрим количество жидкости, прошедшее через точку «а»
наш домен через какое-то время t . Объем = А * V * т Проверка единиц измерения дает площадь x длина/время x время = площадь x длина =
объем. Таким образом, масса в точке «а» ma равна просто плотности r .
умножить объем на «а». ма = (r * A * V * t)a Если мы сравним поток через другую точку области, точка
«b», за то же время t , находим массу в «b» мб будет
плотность, умноженная на скорость, умноженная на площадь, умноженная на время в точке «b»: mb = (r * A * V * t)b Из закона сохранения массы эти две массы одинаковы.
и так как
времена одинаковы, мы можем устранить зависимость от времени. (г * А * V) а = (г * А * V) б r * A * V = константа Закон сохранения массы дает нам простой способ определить
скорость потока в трубе, если плотность постоянна. Если мы можем определить (или задать) скорость в некоторой известной области,
уравнение сообщает нам значение скорости для любой другой области. Вот неподвижная версия изображения, которое вы можете использовать в своих собственных
представление этого материала: Навигация .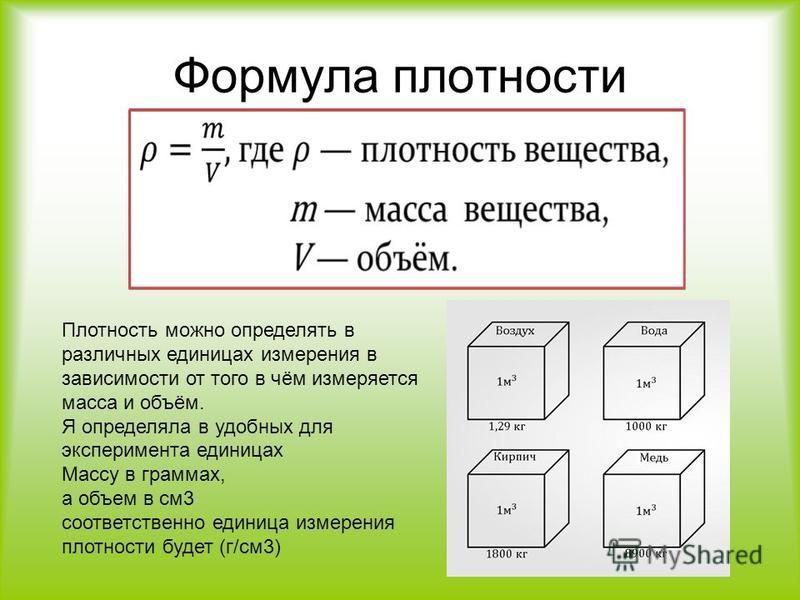 Какое количество массы перешло в энергию при этом процессе? Используя нашу удобную формулу эквивалентности массы и энергии, мы можем определить:
Какое количество массы перешло в энергию при этом процессе? Используя нашу удобную формулу эквивалентности массы и энергии, мы можем определить: Почему объекты имеют массу?
 Когда безмассовые бозоны движутся против этого поля, их импульс замедляется, и они теряют часть энергии.Поле Хиггса преобразует эту энергию в энергию массы, которая проявляется как свойство массы, которое мы измеряем. Было предсказано, что это взаимодействие между бозонами и полем Хиггса создаст новую частицу, крошечный бозон, названный бозоном Хиггса. Ускоритель частиц в ЦЕРНе наконец продемонстрировал существование частицы Хиггса в 2013 году, а 8 октября 2013 года Питер Хиггс и Франсуа Энглер были удостоены Нобелевской премии по физике за свою теоретическую работу над частицей.
Когда безмассовые бозоны движутся против этого поля, их импульс замедляется, и они теряют часть энергии.Поле Хиггса преобразует эту энергию в энергию массы, которая проявляется как свойство массы, которое мы измеряем. Было предсказано, что это взаимодействие между бозонами и полем Хиггса создаст новую частицу, крошечный бозон, названный бозоном Хиггса. Ускоритель частиц в ЦЕРНе наконец продемонстрировал существование частицы Хиггса в 2013 году, а 8 октября 2013 года Питер Хиггс и Франсуа Энглер были удостоены Нобелевской премии по физике за свою теоретическую работу над частицей. Формула массы: определение и примеры — видео и расшифровка урока
Расчет и измерение массы
 Первый метод включает в себя некоторую математику. Масса вводится в физику в Второй закон движения Ньютона . В этом законе Ньютон утверждает, что если сложить все силы, действующие на объект, называемые суммой сил или чистой силой, и эта сумма не равна нулю, то этот объект ускоряется.Этот закон гласит, что сила, действующая на объект, пропорциональна ускорению, испытываемому объектом. Это означает, что если сила увеличивается, то увеличивается ускорение, и наоборот, если сила уменьшается, то уменьшается ускорение. Константа пропорциональности между силой и ускорением называется массой. Более конкретно, она называется инерционной массой.
Первый метод включает в себя некоторую математику. Масса вводится в физику в Второй закон движения Ньютона . В этом законе Ньютон утверждает, что если сложить все силы, действующие на объект, называемые суммой сил или чистой силой, и эта сумма не равна нулю, то этот объект ускоряется.Этот закон гласит, что сила, действующая на объект, пропорциональна ускорению, испытываемому объектом. Это означает, что если сила увеличивается, то увеличивается ускорение, и наоборот, если сила уменьшается, то уменьшается ускорение. Константа пропорциональности между силой и ускорением называется массой. Более конкретно, она называется инерционной массой. Эта система уравнений дает нам формулу для расчета массы объекта, если мы знаем действующую на него силу и ускорение объекта:
Эта система уравнений дает нам формулу для расчета массы объекта, если мы знаем действующую на него силу и ускорение объекта: Ускорение равно 0,5 метра в секунду в квадрате. Метры в секунду в квадрате уравновешивают друг друга, и мы затем делим 8 на 0,5, что означает, что мы получаем массу 16 килограммов. Как видите, если вы знаете силу, действующую на объект, и ускорение, возникающее в результате этой силы, вы сможете вычислить массу объекта.
Ускорение равно 0,5 метра в секунду в квадрате. Метры в секунду в квадрате уравновешивают друг друга, и мы затем делим 8 на 0,5, что означает, что мы получаем массу 16 килограммов. Как видите, если вы знаете силу, действующую на объект, и ускорение, возникающее в результате этой силы, вы сможете вычислить массу объекта. Затем вы можете определить массу большого объекта.
Затем вы можете определить массу большого объекта. Резюме урока
Калькулятор плотности p = м/В
Использование калькулятора
Уравнение плотности для этих расчетов:
р = плотность
м = масса
В = объем Калькулятор может использовать любые два значения для расчета третьего. Плотность определяется как масса на единицу объема. Наряду со значениями введите известные единицы измерения для каждого, и этот калькулятор будет конвертировать между единицами.
Калькулятор может использовать любые два значения для расчета третьего. Плотность определяется как масса на единицу объема. Наряду со значениями введите известные единицы измерения для каждого, и этот калькулятор будет конвертировать между единицами. Значимые цифры
Расчет плотности:
Рассчитать плотность по массе и объему.
Рассчитать массу по плотности и объему.
Рассчитать объем по плотности и массе.
Сохранение массы
 »
» Если жидкость проходит через
площадь A при скорости V , мы можем определить объем Vol быть:
Если жидкость проходит через
площадь A при скорости V , мы можем определить объем Vol быть: В нашем
анимации, площадь «b» составляет половину площади «a». Следовательно,
скорость в точке «b» должна быть в два раза больше скорости в точке «a». Если мы желаем
определенной скорости в трубе, мы можем определить площадь, необходимую для
получить эту скорость.Эта информация используется при разработке
аэродинамические трубы. Количество плотность
умноженная на площадь умноженная на скорость имеет размерность масса/время и равна
называется массовым расходом . Это количество
является важным параметром при определении
тяга, создаваемая двигателем
система.
По мере приближения скорости потока к
скорость звука плотность
поток больше не является константой, и тогда мы должны использовать
сжимаемая форма
уравнения массового расхода.
Уравнение сохранения массы имеет место и в дифференциальном
формируются как часть
Уравнения Навье-Стокса
потока жидкости.
В нашем
анимации, площадь «b» составляет половину площади «a». Следовательно,
скорость в точке «b» должна быть в два раза больше скорости в точке «a». Если мы желаем
определенной скорости в трубе, мы можем определить площадь, необходимую для
получить эту скорость.Эта информация используется при разработке
аэродинамические трубы. Количество плотность
умноженная на площадь умноженная на скорость имеет размерность масса/время и равна
называется массовым расходом . Это количество
является важным параметром при определении
тяга, создаваемая двигателем
система.
По мере приближения скорости потока к
скорость звука плотность
поток больше не является константой, и тогда мы должны использовать
сжимаемая форма
уравнения массового расхода.
Уравнение сохранения массы имеет место и в дифференциальном
формируются как часть
Уравнения Навье-Стокса
потока жидкости.
Деятельность:
Экскурсии с гидом  .
. Расчет масс-молей Учебное пособие по химии
Ключевые понятия
⚛ 1 моль чистого вещества имеет массу, равную его молекулярной массе (1) , выраженной в граммах.
· Известна как молярная масса M и выражается в г моль -1
(г/моль, грамм на моль вещества)
⚛ Связь между молярной массой, массой и молями может быть выражена в виде математического уравнения, как показано ниже:
г моль -1 = г ÷ моль
молярная масса = масса ÷ моль
М = м ÷ п
где:
M = молярная масса чистого вещества (измеряется в г моль -1 )
m = масса чистого вещества (измеряется в граммах, г)
n = количество чистого вещества (измеряется в молях, моль)
⚛ Это математическое уравнение можно преобразовать, чтобы получить следующее:
(i) п = м ÷ М
моль = масса ÷ молярная масса
(ii) m = n × M
масса = моли × молярная масса
⚛ Для расчета молей чистого вещества: n = m ÷ M
⚛ Для расчета массы чистого вещества: m = n × M
⚛ Для расчета молярной массы чистого вещества: M = m ÷ n
Пожалуйста, не блокируйте рекламу на этом сайте.
Нет рекламы = нет денег для нас = нет бесплатных вещей для вас!
Расчет массы чистого вещества (m=nM)
1 моль чистого вещества определяется как масса в граммах, равная его относительной молекулярной массе.
Эта величина известна как молярная масса (символ М).
Итак, масса 1 моля чистого вещества = относительная молекулярная масса в граммах
А, масса 1 моля чистого вещества = молярная масса чистого вещества (г моль -1 )
или масса 1 моля = M (г моль -1 )
В таблице ниже указана масса 1 моля ряда обычных чистых веществ:
| Имя | Молекулярная Формула | Молярная масса (G MOL -1 ) | Масса 1 моль (G) | |
|---|---|---|---|---|
| Гелиевый газ | HE | 4.003 | 4.003 G Mol -1 | 4003 г |
| Кислородный газ | O 2 | 2 × 16. 00 = 32.00 00 = 32.00 | 32.00 G Mol -1 | 32.00 G |
| Диоксид углекислого газа | CO 2 | 12.01 + (2 × 16.00) = 44.01 | 44,01 г моль 2-1 | 44,01 г |
| жидкая вода | H 2 o | (2 × 1,008) + 16.00 = 18,016 | 18,016 г-моль -1 | 18,016 г |
Из таблицы видно, что 1 моль воды имеет массу 18,016 грамма, что не так уж и много (примерно масса воды в паре маленьких кубиков льда, которые можно приготовить в семейном морозильнике).
А что, если бы у вас было 10 молей воды? Какова будет масса 10 молей воды?
Если 1 моль воды имеет массу 18,016 г, то 10 моль воды должны иметь массу в десять раз больше:
масса 10 молей воды = 10 × масса 1 моля воды
масса 10 молей воды = 10×18.016 = 180,16 г (около массы воды, которую можно налить в маленький стакан)
Итак, если бы у нас было только ½ моля воды, какая масса воды была бы у нас?
Если 1 моль воды имеет массу 18,016 г, то ½ моля воды должно иметь ½ массы:
масса ½ моля воды = ½ × масса 1 моля воды
масса ½ моля воды = ½ × 18,016 = 9,008 г
В обоих приведенных выше примерах мы можем рассчитать массу воды в граммах, умножив количество молей воды на массу 1 моля воды в граммах:
масса воды = моль воды × масса 1 моля воды
, так как масса 1 моля воды в граммах известна как его молярная масса, мы можем записать:
масса воды = моли воды × молярная масса воды
В таблице ниже сравниваются массы различных количеств воды в молях:
| масса воды (г) | = | моль воды (моль) | × | масса 1 моля воды (молярная масса воды) (г·моль 90) | |
|---|---|---|---|---|---|
| 0 | = | 0.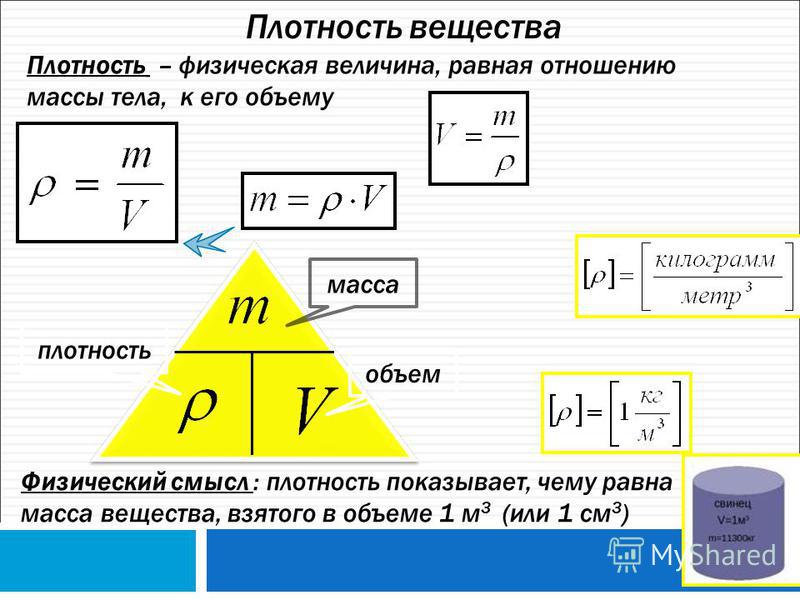 00 00 | × | 18,016 | |
| 9,008 | = | 0,50 | × | 18,016 | |
| 18,016 | = | 1,00 | × | 18,016 | |
| 27,024 | = | 1.50 | × | 18.016 | 18.016 |
| 180.16 | = | 10.00 | × | 18.016 | |
| 270.24 | = | 15,00 | × | 18,016 |
Из данных таблицы можно обобщить и сказать, что для любого чистого вещества масса вещества в граммах равна количеству молей вещества, умноженному на массу 1 моля вещества:
масса = моли × масса 1 моля
и так как масса 1 моля вещества (в граммах) = молярная масса (в граммах на моль)
масса (г) = моли × молярная масса (г моль -1 )
м = п × М
где
m = масса чистого вещества в граммах
n = количество чистого вещества в молях
M = молярная масса чистого вещества в граммах на моль
Мы также можем нанести данные из таблицы выше на график, как показано ниже:
| масса (г) | 051015300250200150100500 |
| молей (моль) |
На приведенном выше графике показана прямая линия, проходящая через начало координат (0,0), поэтому уравнение для линии:
y = наклон × x
где:
y масса воды (г)
x моль воды (моль)
наклон (градиент) линии = вертикальный подъем ÷ горизонтальный ход
Мы можем определить наклон линии, используя 2 точки на прямой, например, (0,0) и (15. 0, 270,24):
0, 270,24):
наклон = (270,24 г — 0 г) ÷ (15 моль — 0 моль) = 18,016 г моль -1
Поскольку 18,016 г моль -1 является молярной массой воды, мы можем сказать:
наклон = молярная масса воды (г моль -1 )
Следовательно, уравнение для этой линии:
Масса(H 2 O) = молярная масса (H 2 O) × количество молей (H 2 O)
В целом:
масса (г) = молярная масса (г моль -1 ) × моль (моль)
Из данных таблицы и ее графического представления можно обобщить и сказать, что для любого чистого вещества масса вещества в граммах равна количеству молей вещества, умноженному на массу 1 моля вещества:
масса = моли × масса 1 моля
и так как масса 1 моля вещества (в граммах) = молярная масса (в граммах на моль)
масса (г) = моли × молярная масса (г моль -1 )
м = п × М
Выполните следующие шаги, чтобы рассчитать массу чистого вещества, зная количество вещества в молях:
Шаг 1. Извлечь данные из вопроса:
Извлечь данные из вопроса:
масса = м = ? (единицы измерения граммы)
крота = n = запишите, что вам говорят в вопросе
молярная масса = M = запишите то, что вам сказали в вопросе (единицы измерения: г моль -1 )
(возможно, вам потребуется рассчитать это, используя молекулярную формулу чистого вещества и периодическую таблицу)
Шаг 2. Проверить единицы на согласованность и при необходимости преобразовать:
Количество вещества должно быть в молях (моль) !
Если количество указано в миллимолях (ммоль), разделите его на 1000, чтобы получить количество в молях (моль).
Если количество указано в микромолях (мкмоль), разделите его на 1 000 000, чтобы получить количество в молях (моль).
Если количество указано в киломолях (кмоль), умножьте его на 1000, чтобы получить количество в молях (моль).
Шаг 3. Напишите математическое уравнение (математическую формулу):
масса = моли × молярная масса
или
м = п × М
Шаг 4. Подставьте значения и решите уравнение, чтобы найти значение массы m в граммах (г).
Подставьте значения и решите уравнение, чтобы найти значение массы m в граммах (г).
↪ Наверх
Расчет молей чистого вещества (n=m/M)
В ходе обсуждения выше мы обнаружили, что можем рассчитать массу чистого вещества, используя моли и молярную массу вещества:
масса (г) = моли (моль) × молярная масса (г моль -1 )
Как бы мы рассчитали количество молей чистого вещества, если бы знали массу этого вещества?
(a) Мы могли бы использовать некоторую алгебру: разделить обе части уравнения на молярную массу:
| MASS | = | молей × |
| молярная масса | |
моль = масса ÷ молярная масса
н = м ÷ М
или
(б) Мы могли бы использовать некоторую логику:
| знаем массу в единицах | грамм (г) |
| знаем молярную массу в единицах | грамм на моль (г моль -1 ) | моль (моль) |
При рассмотрении единиц мы видим, что деление молярной массы на массу даст нам количество в единицах «моль -1 »
молярная масса/масса = г моль -1 / г = моль -1
Если мы перевернем это с ног на голову (в математических терминах, возьмем обратное), мы получим количество с единицами «моль», что и нужно:
масса/молярная масса = г / г моль -1 = моль
так
моль = масса ÷ молярная масса
н = м ÷ М
Выполните следующие шаги, чтобы рассчитать количество чистого вещества в молях, учитывая массу вещества:
Шаг 1. Извлечь данные из вопроса:
Извлечь данные из вопроса:
масса = m = запишите, что вам сказали в вопросе
моля = n = ? (единицы моль)
молярная масса = M = запишите то, что вам сказали в вопросе (единицы измерения: г моль -1 )
(возможно, вам потребуется рассчитать это, используя молекулярную формулу чистого вещества и периодическую таблицу)
Шаг 2. Проверить единицы на согласованность и при необходимости преобразовать:
Масса должна быть в граммах!
Если масса указана в миллиграммах (мг), разделите ее на 1000, чтобы получить массу в граммах (г).
Если масса указана в микрограммах (мкг), разделите ее на 1 000 000, чтобы получить массу в граммах (г).
Если масса указана в килограммах (кг), умножьте ее на 1000, чтобы получить массу в граммах (г).
Шаг 3. Напишите математическое уравнение (математическую формулу):
моль = масса ÷ молярная масса
или
н = м ÷ М
Шаг 4. Подставьте значения и решите уравнение, чтобы найти количество молей вещества (моль).
↪ Наверх
Расчет молярной массы чистого вещества (M=m/n)
Что, если бы вы знали количество чистого вещества в молях и его массу?
Не могли бы вы вычислить его молярную массу?
Напомним, что масса = моли × молярная масса или m = n × M
(a) Мы могли бы использовать некоторую алгебру: разделить обе части уравнения на моли:
| MASS | = | |
| моль | |
молярная масса = масса ÷ моль
М = м ÷ п
или (б) Мы могли бы использовать некоторую логику:
Изучая единицы измерения, мы видим, что, разделив массу в граммах на количество в молях, мы получим количество в граммах на моль (г-моль -1 ), которые являются единицами измерения молекулярной массы.
Следовательно, молярная масса (г моль -1 ) = масса (г) ÷ моль (моль)
или можно написать
М = м ÷ п
Выполните следующие шаги, чтобы рассчитать молярную массу чистого вещества, зная количество вещества в молях и массу вещества:
Шаг 1. Извлечь данные из вопроса:
масса = m = запишите, что вам сказали в вопросе
крота = n = запишите, что вам говорят в вопросе
молярная масса = M = ? (единицы г моль -1 )
Шаг 2. Проверить единицы на согласованность и при необходимости преобразовать:
Масса должна быть указана в граммах (г)!
Количество, моли, должно быть указано в молях (моль)!
Шаг 3. Напишите математическое уравнение (математическую формулу):
молярная масса = масса ÷ моль
или
М = м ÷ п
Шаг 4. Подставьте значения и решите уравнение, чтобы найти молярную массу вещества в граммах на моль.
↪ Наверх
Примеры расчета массы, молей, молярной массы
В каждом из приведенных ниже рабочих примеров вам будет предложено рассчитать моль, массу или молярную массу чистого вещества.
Чтобы правильно ответить на каждый вопрос, вам необходимо:
- Шаг 1. Извлечение информации из вопроса
- Шаг 2. Проверить данные на согласованность единиц
- Шаг 3. Выберите математическое уравнение, чтобы найти неизвестное
- Шаг 4. Подставьте свои значения в уравнение и решите
Рабочий пример: масса = моли × молярная масса (m=n×M)
Вопрос: Рассчитайте массу 0,25 моль воды, H 2 O.
Решение:
Шаг 1. Извлечь данные из вопроса:
моль = n = 0,25 моль
молярная масса = M = (2 × 1,008) + 16,00 = 18,016 г моль -1
(Рассчитано с использованием периодической таблицы)
масса = м = ? г
Шаг 2. Проверить данные на непротиворечивость:
Количество воды в молях (моль)? да.
Нам не нужно конвертировать это.
Шаг 3. Напишите математическое уравнение (математическую формулу):
масса = моли × молярная масса
или
м = п × М
Шаг 4. Подставьте значения в уравнение и найдите массу (г):
масса = m = 0,25 моль × 18,016 г моль -1 = 4,5 г
(обоснованы только 2 значащие цифры)
Рабочий пример: моли = масса &делим молярную массу (n=m/M)
Вопрос: Рассчитайте количество газообразного кислорода O 2 в молях, содержащегося в 124.5 г газообразного кислорода.
Решение:
Шаг 1. Извлечь данные из вопроса:
масса = m = 124,5 г
молярная масса = M = 2 × 16,00 = 32,00 г моль -1
(Рассчитано с использованием периодической таблицы)
моля = n = ? моль
Шаг 2. Проверить данные на непротиворечивость:
Масса газообразного кислорода указана в граммах (г)? да.
Нам не нужно конвертировать это.
Шаг 3. Напишите математическое уравнение (математическую формулу):
моль = масса ÷ молярная масса
или
н = м ÷ М
Шаг 4. Подставьте значения в уравнение и решите, чтобы найти моли газообразного кислорода:
моль = n = 124,5 г ÷ 32,00 г моль -1 = 3.891 моль
(обоснованы 4 значащие цифры)
Рабочий пример: молярная масса = масса ÷ моль (M=m/n)
Вопрос: Рассчитайте молярную массу чистого вещества, если 1,75 моль вещества имеет массу 29,79 г.
Решение:
Шаг 1. Извлечь данные из вопроса:
масса = m = 29,79 г
моля = n = 1.75 моль
Шаг 2. Проверить данные на непротиворечивость:
Масса в граммах (г)? да. Нам не нужно конвертировать это.
Количество вещества указано в молях (моль)? да. Нам не нужно конвертировать это.
Шаг 3. Напишите уравнение:
молярная масса = масса ÷ моль
или
М = м ÷ н
Шаг 4. Подставьте значения в уравнение и решите молярную массу:
молярная масса = M = 29,79 г ÷ 1,75 моль = 17,0 г моль -1
(обоснованы 3 значащие цифры)
↪ Наверх
Решение задач с использованием молей, массы и молекулярной массы
Проблема: Карбонат кальция, CaCO 3 , является важным промышленным химикатом.У Химика Криса есть неочищенный образец карбоната кальция.Масса нечистого образца составляет 0,1250 кг, и он состоит из 87,00% (по массе) карбоната кальция. Прежде чем Крис сможет использовать этот карбонат кальция в химической реакции, Крису необходимо знать количество карбоната кальция в молях, присутствующее в этом образце.
Рассчитайте количество карбоната кальция в молях, присутствующее в этом нечистом образце карбоната кальция.
Решение проблемы с использованием модели StoPGoPS для решения проблемы:
| СТОП! | Сформулируйте вопрос. | Какой вопрос просит вас сделать? Рассчитайте количество карбоната кальция в молях n(CaCO 3 ) = моли карбоната кальция = ? моль |
| ПАУЗА! | Пауза для планирования. | Какой химический принцип вам нужно применить? Применение стехиометрии (n = m ÷ M) Какую информацию (данные) вам предоставили? Каков ваш план решения этой проблемы? (i) Напишите математическое уравнение для расчета количества молей карбоната кальция: n(моль) = м(г) ÷ M(г моль -1 ) (ii) Рассчитайте массу карбоната кальция в образце в килограммах (кг). масса карбоната кальция (кг) = 87,00% массы образца (кг) м (CaCO 3 ) в килограммах = ( 87,00/100 ) × м (образец) (iii) Перевести массу карбоната кальция в килограммах (кг) в массу в граммах (г) m(CaCO 3 ) в граммах = m(CaCO 3 ) в кг × 1000 г/кг (iv) Рассчитайте молярную массу карбоната кальция молярная масса = M(CaCO 3 ) = M(Ca) + M(C) + [3 × M(O)] = (v) Подставьте значения m(CaCO 3 ) в граммах и M(CaCO 3 ) в г молях -1 в математическое уравнение и найдите n (моль) n(моль) = м(г) ÷ M(г моль -1 ) |
| ВПЕРЕД! | Следуйте плану. | (i) Напишите математическое уравнение для расчета молей карбоната кальция: n(моль) = м(г) ÷ M(г моль -1 ) n(CaCO 3 ) = m(CaCO 3 ) ÷ M(CaCO 3 ) (ii) Рассчитайте массу карбоната кальция в образце в килограммах (кг). масса карбоната кальция (кг) = 87,00% массы образца (кг) м(CaCO 3 ) в килограммах = ( 87.00/100 ) × м (образец) м (CaCO 3 ) в килограммах = ( 87,00/100 ) × 0,1250 кг = 0,10875 кг (iii) Перевести массу карбоната кальция в килограммах (кг) в массу в граммах (г) m(CaCO 3 ) в граммах = m(CaCO 3 ) в кг × 1000 г/кг м (CaCO 3 ) в граммах = 0,10875 кг × 1000 г/кг = 108.75 г (iv) Рассчитайте молярную массу карбоната кальция молярная масса = M(CaCO 3 ) = M(Ca) + M(C) + [3 × M(O)] M(CaCO 3 ) = 40,08 + 12,01 + [3 × 16,00] = 40,08 + 12,01 + 48,00 = 100,09 г моль -1 (v) Подставьте значения m(CaCO 3 ) в граммах и M(CaCO 3 ) в г молях -1 в математическое уравнение и найдите n (моль) n(CaCO 3 ) = m(CaCO 3 ) ÷ M(CaCO 3 ) n(CaCO 3 ) = m(CaCO 3 ) ÷ M(CaCO 3 ) = 108.75 (обоснованы 4 значащие цифры) |
| ПАУЗА! | Подумайте о правдоподобии. | Вы ответили на заданный вопрос? Да, мы рассчитали количество молей карбоната кальция в образце. Разумно ли ваше решение вопроса? Давайте вернемся назад, чтобы увидеть, дадут ли рассчитанные нами моли карбоната кальция правильную массу образца. Поскольку это приблизительное значение массы образца примерно равно массе образца, указанной в вопросе, мы достаточно уверены в правильности нашего ответа. |
| СТОП! | Укажите решение. | Сколько молей карбоната кальция содержится в образце? н (CaCO 3 ) = 1,087 моль |
↪ Наверх
Пример вопроса: моли, масса и молярная масса
Определите массу в граммах 0,372 моля твердой ромбической серы (S 8 ).
↪ Наверх
Сноски:
(1) Молекулярная масса также известна как молекулярная масса, формульная масса или формульная масса
↪ Вернуться к ключевым понятиям
Существует ли точная формула, определяющая увеличение массы за счет увеличения скорости, как это описано в теории относительности?
Автор вопроса: Тим М.
Ответить
Прежде чем я отвечу на ваш вопрос, я хотел бы начать с более подробного версия известного уравнения Эйнштейна, E = mc 2 .Обычно пишут так:где E – энергия рассматриваемого объекта, m 0 – его масса покоя, c – скорость света, а гамма () — числовой коэффициент, зависящий от скорости. То выражение для гаммы
где v — скорость объекта. При очень малых скоростях гамма составляет примерно равен единице. При скоростях, близких к скорости света, гамма становится больше и больше (попробуйте подставить несколько цифр и посмотрите).Вы уже можете понять, почему массивный частица никогда не сможет двигаться со скоростью света: потребуется бесконечное количество энергии, и ни один двигатель во Вселенной не может обеспечить такую мощность!
Теперь я отвечу на ваш вопрос. Эйнштейн интерпретировал комбинацию gamma * m 0 как быть массой движущегося объекта. Поэтому уравнение обычно цитируется просто как E = mc 2 . Уравнение, связывающее массу со скоростью, имеет вид
Масса, как и гамма, растет со скоростью.Когда объект приближается к скорости света, масса стремится к бесконечности!
Я должен предостеречь: многие физики просто называют m 0 массой, сбрасывая различие между массой покоя и массой Эйнштейна, зависящей от скорости. Так будь обратите внимание, какое определение используется!
Вероятно, эту взаимосвязь можно найти в большинстве вводных учебников по физике в колледже. Хорошая книга для получения более подробной информации на более техническом уровне — Ray Книга Д’Инверно «Введение в теорию относительности Эйнштейна».
Чуть более техническое отступление:
Интересно посмотреть на поведение гаммы при малых скоростях. Это может можно сделать с помощью метода исчисления, называемого расширением Тейлора. Проконсультируйтесь с любым текст исчисления, если вы хотите точно увидеть, что это такое и как это делается. Если мы Тейлор расширяем гамму вокруг v = 0, получаем
Для малых скоростей члены порядка 4 и выше чрезвычайно малы по сравнению с до члена 2-го порядка, поэтому мы можем пренебречь ими всеми вместе.Подключаю это выражение обратно в уравнение Эйнштейна дает
Первый член — это просто масса покоя объекта. Второй срок вы можете признать кинетической энергией классической ньютоновской физики.

 Следовательно, вес Сэма на другой планете = 38 % × его вес на Земле = 0,38 × 1000 фунтов = 380 фунтов 90 003.
Следовательно, вес Сэма на другой планете = 38 % × его вес на Земле = 0,38 × 1000 фунтов = 380 фунтов 90 003.