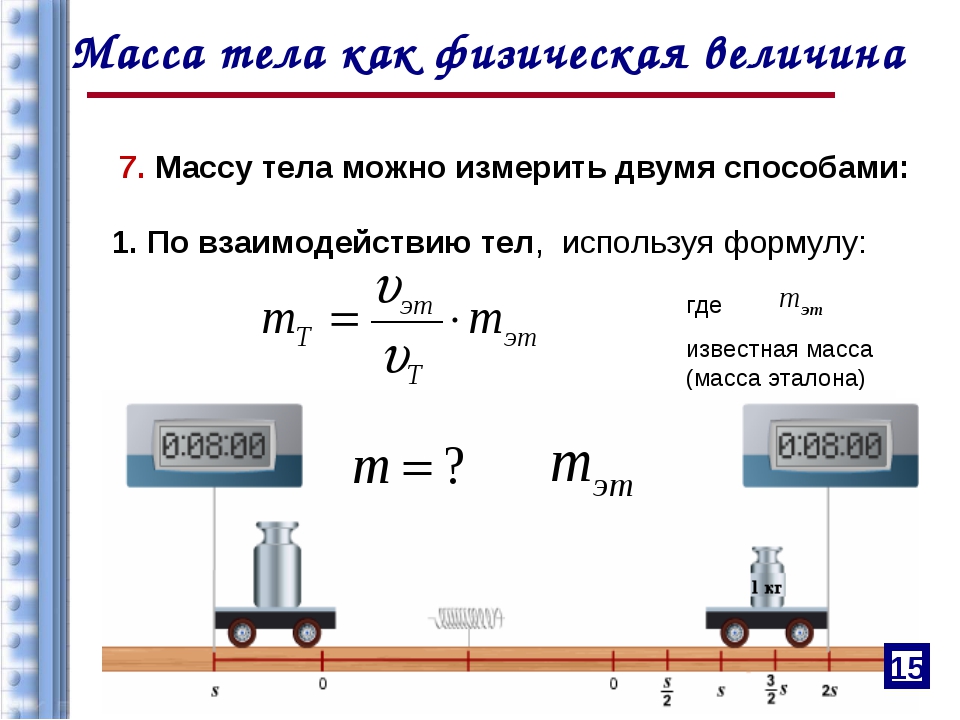
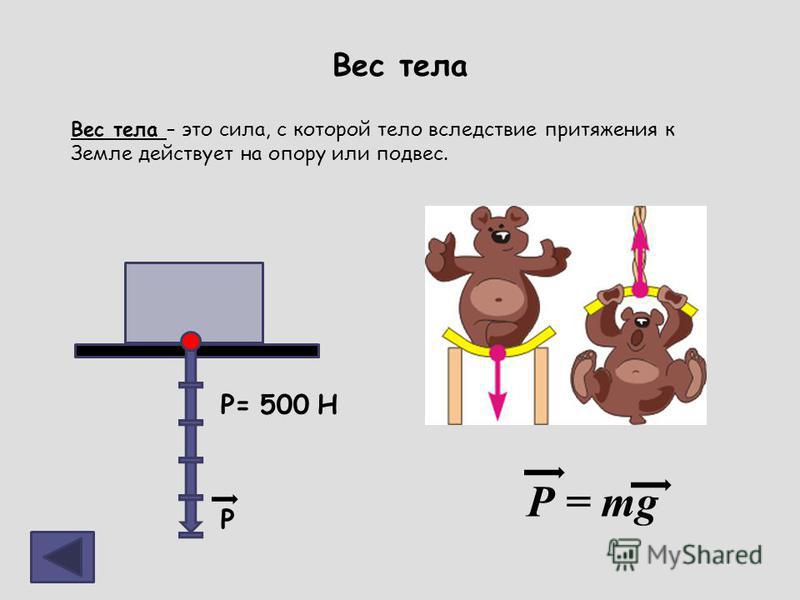
Урок-лекция «Вес тела, движущегося с ускорением»
Цели урока:
- Повторить понятия изученных сил (тяжести, упругости, веса покоящегося тела).
- Повторить формулы этих сил.
- Вывести формулы для веса тела движущегося с ускорением вертикально вверх и вниз.
- Закрепить их на примерах из жизни.
- Сформировать представления учащегося, где эти знания применяются.
Оборудование урока:
- картонки на магнитной доске с указанием сил.
- динамометр, набор грузов на столе у каждого учащегося и у учителя.
Ход урока
- Организационный момент (3-5 мин)
- Проговаривание цели урока и темп урока, для чего эту тему вы выбрали.
А) Повторяем рани изученные темы (7-10 мин)
Сила упругости – Что ребята вы знаете о Fупр.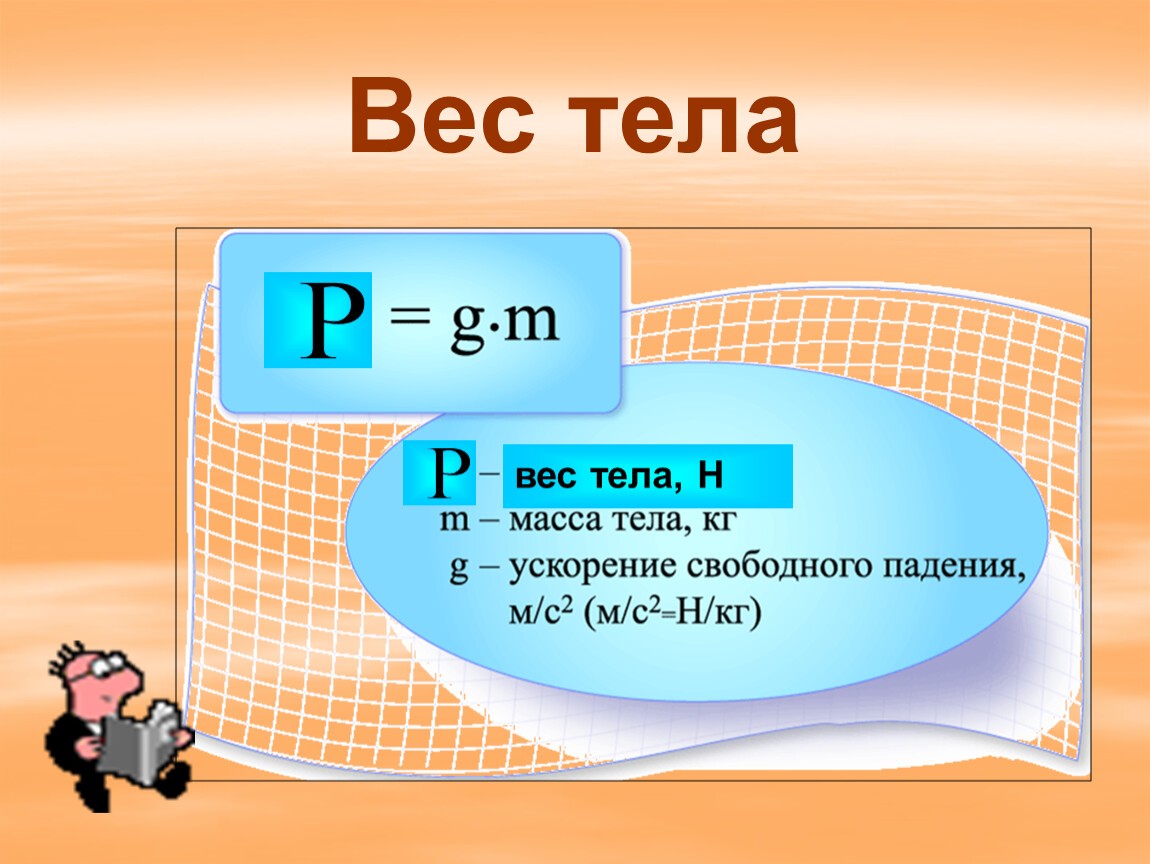
План ответа:
а) что называется силой упругости.
б) когда возникает сила упругости.
в) куда направлена.
г) чему пропорциональна, формула.
Сила тяжести – Что ребята вы знаете о Fтяж.?
а) что называется?
б) куда направлена.
в) от чего зависит? Формула.
е) что такое g? g = ? Особенности g ?
ж) к чему прикладывается? Куда направлена?
Вес тела
а) что называется весом покоящегося тела?
б) какая природа этой силы?в) на что действует? (к чему приложена)
г) формула.
P = mg – если тело покоится или равномерно движется.
Б) P = mg и F = mg
– Одинаковы ли эти силы?
- разная природа
- действуют на разные тела
- различны точки приложения.
В) работа с карточками (они повешены на магнитной доске)
Вопросы:
- Какая сила изображена?
- Чем отличаются изображённые силы?
Г) От чего зависит
Fт ? — зависит от m тела
Fу? — зависит от x-удлинения
P ? — от массы тела, при условии
- Новый материал:
Выясним, что происходит с (весом), когда тело движется по вертикали вниз.
Учащиеся самостоятельно проделывают опыт на столах и убеждаются в результате опыта.
Учитель проговаривает: а) учащиеся держат динамометр с грузом в руке
— Что происходит под действием груза?
— Какие силы возникают?
— Чему по модулю равен вес?
— Сравнить можно силы только … (одной природы)
— Что происходит со стрелкой динамометра, когда опускают динамометр с грузом вниз?
— Стрелка возвращается на «0» т.е. вес уменьшается.
— Докажем это.
Сделаем рисунок, обозначим все действующие силы.
— Выберем ось по направлению ускорения.
— Какой закон описывает это движение?
— Какие силы действуют?
Запишем уравнение второго закона Ньютона.
Fт + Fy = ma
Оy: Fт — Fy = ma
mg — Fy = ma
Fy = — ma + mg
m(g – a) = P
Чему равна проекция вектора, как она определяется? | Fy | = | P |
Вес уменьшился, т. е. P0 = mg > P = m(g – a), так как g > (g – a)
е. P0 = mg > P = m(g – a), так как g > (g – a)
Вывод (сами учащиеся формируют):
Если тело вместе с опорой или подвесом движется с ускорением, которое направлено вниз, то его вес уменьшается по сравнению с весом покоящегося тела.
— Это тело двигалось по вертикали, а изменится ли вес тела движущегося по окружности?
Задача:
Автомобиль массой m движется по выпуклому мосту, радиусом r, со скоростью v. Чему равен вес автомобиля в верхней точке моста.
Учащийся сам выполняет эту задачу у доски, проговаривая каждый шаг.
Оy: mg – N = ma
N = m (g – a)
Вывод: Если тело движется по выпуклой окружности вниз, то его вес уменьшается по сравнению с весом покоящегося тела.
Рассмотрим второй способ движения.
Когда груз вместе с динамометром движется вверх.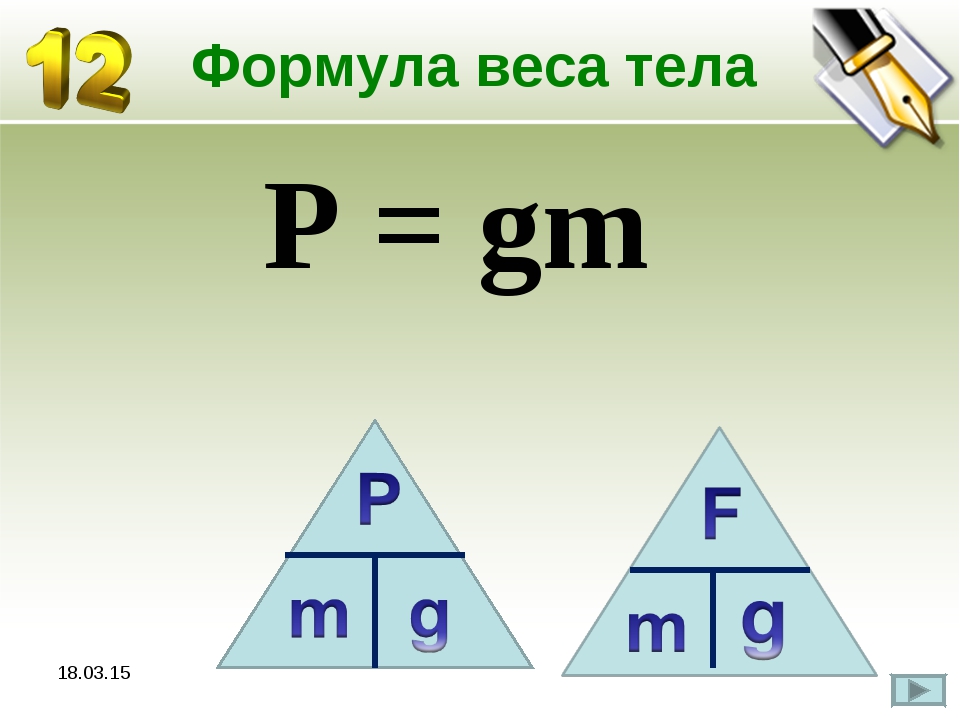 Учащиеся самостоятельно проделывают этот опыт и убеждаются, что стрелка отклоняется вниз.
Учащиеся самостоятельно проделывают этот опыт и убеждаются, что стрелка отклоняется вниз.
— Что пронаблюдали?
Меняется Fy т. е. меняется и P – он увеличивается – докажем.
Запишем II закон Ньютона – уравнение
Fy — Fт = ma
Оy: — Fy + mg = — ma
mg + ma = Fy | Fy | = | P |
m (g + a) = P
Сравним P0= mg и P = m(g + a)
P0 < P т.к. g < (g + a)
Вывод (дети сами): Если тело движется с ускорением вверх, то его вес больше веса покоящегося тела.
— Может ли уменьшиться вес тела, движущегося по окружности? (да)
— А в какой точке больше в верхней или в нижней?
Задача:
Рассчитать вес летчика массой m, выводящего самолёт из пикирования со скоростью v, и радиусом окружности r?
Учащиеся самостоятельно выполняют эту задачу, один у доски проговаривая каждый шаг.
Оy: — mg + N = ma | N | = | P |
P = m (g + a) a = v2/R
Вывод: вес лётчика увеличится.
Если вес человека, в данном случае лётчика, увеличивается, при движении вверх, то этот человек испытывает перегрузку.
Привести примеры перегрузки.
а) космонавт при старте ракеты – испытывает 10P0.
— Мы с вами на поверхности Земли можем испытывать перегрузку?
б) качели – «лопенги».
в) поднимаемся на 5-й, 9-й этажи.
г) прыгаем на физкультуре, подымаемся по шведской стенке.
Но эти перегрузки незначительны.
Рассмотрим ещё один вид движения.
Опыт (проделывают учащиеся самостоятельно и наблюдают):
Динамометр с грузом подняли и выпустили из рук. Что произошло со стрелкой?
Что произошло со стрелкой?
— Она вернулась на «0»?
— Что это значит?
Нет Fy = 0 > P = 0 т. е. вес отсутствует.
Это явление называется невесомостью.
— При каком условии P = 0 – свободном падении. т. е. а = g
P = (g – g) = 0.
Каждый из вас был на поверхности Земли в состоянии невесомости (прыжки с вышки).
- Итог урока.
Итак, мы с вами сегодня на уроке вывели формулы веса тел движущихся вертикально вверх и вниз, и увидели, что при подъёме вверх вес увеличивается, а при опускании вниз вес уменьшается. Вывести алгоритм таких задач и всё это закрепили.
Д/з: § 30 (II ч) – 31. упр. 15 (2).
Спасибо за урок!
До свидания.
Сила веса тела определение и формула.
 Сила веса, формулы
Сила веса, формулыВ данном параграфе мы напомним Вам о силе тяжести, центростримительном ускорение и весе тела
На каждое тело, находящееся на планете, действует гравитация Земли . Сила, с которой Земля притягивает каждое тело, определяется по формуле
Точка приложения находится в центре тяжести тела. Сила тяжести всегда направлена вертикально вниз .
Силу, с которой тело притягивается к Земле под действием поля тяготения Земли, называют силой тяжести. По закону всемирного тяготения на поверхности Земли (или вблизи этой поверхности) на тело массой m действует сила тяжести
F т =GMm/R 2
где М — масса Земли; R — радиус Земли.
Если на тело действует только сила тяжести, а все другие силы взаимно уравновешены, тело совершает свободное падение. Согласно второму закону Ньютона и формуле
F
т =GMm/R
2 модуль ускорения свободного падения g находят по формуле
g=F т /m=GM/R 2 .
Из формулы (2. 29) следует, что ускорение свободного падения не зависит от массы m падающего тела, т.е. для всех тел в данном месте Земли оно одинаково. Из формулы (2.29) следует, что Fт = mg. В векторном виде
29) следует, что ускорение свободного падения не зависит от массы m падающего тела, т.е. для всех тел в данном месте Земли оно одинаково. Из формулы (2.29) следует, что Fт = mg. В векторном виде
F т =mg
В § 5 было отмечено, что поскольку Земля не шар, а эллипсоид вращения, ее полярный радиус меньше экваториального. Из формулы F т =GMm/R 2 видно, что по этой причине сила тяжести и вызываемое ею ускорение свободного падения на полюсе больше, чем на экваторе.
Сила тяжести действует на все тела, находящиеся в поле тяготения Земли, однако не все тела падают на Землю. Это объясняется тем, что движению многих тел препятствуют другие тела, например опоры, нити подвеса и т. п. Тела, ограничивающие движение других тел, называют
На ускорение свободного падения влияет вращение Земли. Это влияние объясняется так. Системы отсчета, связанные с поверхностью Земли (кроме двух, связанных с полюсами Земли), не являются, строго говоря, инерциальными системами отсчета — Земля вращается вокруг своей оси, а вместе с ней движутся по окружностям с центростремительным ускорением и такие системы отсчета. Эта неинерциальность систем отсчета проявляется, в частности, в том, что значение ускорения свободного падения оказывается различным в разных местах Земли и зависит от географической широты того места, где находится связанная с Землей система отсчета, относительно которой определяется ускорение свободного падения.
Системы отсчета, связанные с поверхностью Земли (кроме двух, связанных с полюсами Земли), не являются, строго говоря, инерциальными системами отсчета — Земля вращается вокруг своей оси, а вместе с ней движутся по окружностям с центростремительным ускорением и такие системы отсчета. Эта неинерциальность систем отсчета проявляется, в частности, в том, что значение ускорения свободного падения оказывается различным в разных местах Земли и зависит от географической широты того места, где находится связанная с Землей система отсчета, относительно которой определяется ускорение свободного падения.
Измерения, проведенные на разных широтах, показали, что числовые значения ускорения свободного падения мало отличаются друг от друга. Поэтому при не очень точных расчетах можно пренебречь неинерциальностью систем отсчета, связанных с поверхностью Земли, а также отличием формы Земли от сферической, и считать, что ускорение свободного падения в любом месте Земли одинаково и равно 9,8 м/с 2 .
Из закона всемирного тяготения следует, что сила тяжести и вызываемое ею ускорение свободного падения уменьшаются при увеличении расстояния от Земли. На высоте h от поверхности Земли модуль ускорения свободного падения определяют по формуле
На высоте h от поверхности Земли модуль ускорения свободного падения определяют по формуле
g=GM/(R+h) 2.
Установлено, что на высоте 300 км над поверхностью Земли ускорение свободного падения меньше, чем у поверхности Земли, на 1 м/с2.
Следовательно, вблизи Земли (до высот нескольких километров) сила тяжести практически не изменяется, а потому свободное падение тел вблизи Земли является движением равноускоренным.
Силу, в которой вследствие притяжения к Земле тело действует на свою опору или подвес, называют весом тела. В отличие от силы тяжести, являющейся гравитационной силой, приложенной к телу, вес — это упругая сила, приложенная к опоре или подвесу (т. е. к связи).
Наблюдения показывают, что вес тела Р, определяемый на пружинных весах, равен действующей на тело силе тяжести F т только в том случае, если весы с телом относительно Земли покоятся или движутся равномерно и прямолинейно; В этом случае
Р=F т =mg.
Если же тело движется ускоренно, то его вес зависит от значения этого ускорения и от его направления относительно направления ускорения свободного падения.
Когда тело подвешено на пружинных весах, на него действуют две силы: сила тяжести F т =mg и сила упругости F yп пружины. Если при этом тело движется по вертикали вверх или вниз относительно направления ускорения свободного падения, значит векторная сумма сил F т и F уп дает равнодействующую, вызывающую ускорение тела, т. е.
F т + F уп =mа.
Согласно приведенному выше определению понятия «вес», можно написать, что Р=-F yп. Из формулы: F т + F уп =mа. с учетом того, что F т =mg, следует, что mg-mа=-F yп . Следовательно, Р=m(g-а).
Силы F т и F уп направлены по одной вертикальной прямой. Поэтому если ускорение тела а направлено вниз (т.е. совпадает по направлению с ускорением свободного падения g), то по модулю
P=m(g-a)
Если же ускорение тела направлено вверх (т. е. противоположно направлению ускорения свободного падения), то
Р = m = m(g+а).
Следовательно, вес тела, ускорение которого совпадает по направлению с ускорением свободного падения, меньше веса покоящегося тела, а вес тела, ускорение которого противоположно направлению ускорения свободного падения, больше веса покоящегося тела. Увеличение веса тела, вызванное его ускоренным движением, называют перегрузкой.
При свободном падении a=g. Из формулы: P=m(g-a)
следует, что в таком случае Р=0, т. е. вес отсутствует. Следовательно, если тела движутся только под действием силы тяжести (т. е. свободно падают), они находятся в состоянии невесомости . Характерным признаком этого состояния является отсутствие у свободно падающих тел деформаций и внутренних напряжений, которые вызываются у покоящихся тел силой тяжести. Причина невесомости тел заключается в том, что сила тяжести сообщает свободно падающему телу и его опоре (или подвесу) одинаковые ускорения.
Изучением различия между массой и весом тела занимался Ньютон. Он рассуждал так: мы прекрасно знаем, что различные вещества, взятые в одинаковых объемах, весят неодинаково.
Масса
Количество вещества, содержащееся в том или ином предмете, Ньютон назвал массой.
Масса — то общее, что присуще всем без исключения предметам, — все равно, будут ли это черепки от старого глиняного горшка или золотые часы.
Например, кусочек золота более чем вдвое тяжелее точно такого же кусочка меди. Вероятно, частички золота, предположил Ньютон, способны укладываться плотнее, чем частички меди, и в золоте умещается больше вещества, чем в таком же по размерам куске меди.
Современные ученые установили, что различная плотность веществ объясняется не только тем, что частицы вещества уложены более плотно. Сами мельчайшие частички — атомы — отличаются по весу друг от друга: атомы золота тяжелее атомов меди .
Лежит ли какой-нибудь предмет неподвижно, или свободно падает на землю, или качается, подвешенный на нитке, — его масса при всех условиях остается неизменной .
Когда мы хотим узнать, как велика масса предмета, мы взвешиваем его на обычных торговых или лабораторных весах с чашками и гирями. На одну чашку весов кладем предмет, а на другую гири и таким образом сравниваем массу предмета с массой гирь. Поэтому торговые и лабораторные весы можно перевозить куда угодно: на полюс и на экватор, на вершину высокой горы и в глубокую шахту. Всюду и везде, даже на других планетах, эти весы будут показывать правильно, потому что с их помощью мы определяем не вес, а массу.
На одну чашку весов кладем предмет, а на другую гири и таким образом сравниваем массу предмета с массой гирь. Поэтому торговые и лабораторные весы можно перевозить куда угодно: на полюс и на экватор, на вершину высокой горы и в глубокую шахту. Всюду и везде, даже на других планетах, эти весы будут показывать правильно, потому что с их помощью мы определяем не вес, а массу.
В разных точках земли можно измерять пружинными весами. Прицепив на крючок пружинных весов какой-либо предмет, мы сравниваем силу притяжения Земли, которую испытывает этот предмет, с силой упругости пружины. Сила тяжести тянет вниз, (подробнее: ) сила пружины — вверх, и, когда обе силы уравновесятся, указатель весов останавливается на определенном делении.
Пружинные весы верны только на той широте, где они изготовлены. Во всех других широтах, на полюсе и на экваторе они будут показывать различный вес. Правда, разница невелика, но она все же обнаружится, потому что сила тяжести на Земле не везде одинакова, а сила упругости пружины, разумеется, остается постоянной.
На других планетах эта разность окажется значительной и заметной. На Луне, например, предмет, весивший на Земле 1 килограмм, потянет на пружинных весах, привезенных с Земли, 161 грамм, на Марсе — 380 граммов, а на огромном Юпитере — 2640 граммов.
Чем больше масса планеты, тем больше и сила, с которой она притягивает тело, подвешенное на пружинных весах .
Поэтому так много весит тело на Юпитере и так мало на Луне.
Задать вопрос ВРАЧУ, и получить БЕСПЛАТНЫЙ ОТВЕТ, Вы можете заполнив на НАШЕМ САЙТЕ специальную форму, по этой ссылке >>>
Как вычислить вес через массу
Вес – сила, с которой тело действует на опору (или другой вид крепления), возникающая в поле силы тяжести. Масса связана с энергией и импульсом тела и эквивалентна энергии его покоя. Масса не зависит от силы тяжести (точнее от ускорения свободного падения). Поэтому тело, на Земле имеющее массу 20 кг, на Луне будет иметь массу 20 кг, но совсем другой вес (потому что ускорение свободного падения на Луне в 6 раз меньше, чем на Земле).
Шаги Править
Часть 1 из 4: Вычисление веса Править
Часть 2 из 4: Примеры задач Править
Часть 3 из 4: Распространенные ошибки Править
Часть 4 из 4: Приложение: вес, выраженный в кгс Править
- Ньютон – это единица измерения силы в международной системе единиц СИ. Нередко сила выражается в килограмм-силах, или кгс (в системе единиц МКГСС). Эта единица очень удобна для сравнения весов на Земле и в космосе.
- 1 кгс = 9,8166 Н.
- Разделите вес, выраженный в ньютонах, на 9,80665.
- Вес космонавта, который «весит» 101 кг (то есть его масса равна 101 кг), составляет 101,3 кгс на Северном полюсе и 16,5 кгс на Луне.
- Международная система единиц СИ – система единиц физических величин, которая является наиболее широко используемой системой единиц в мире.
- Самая трудная задача – уяснить разницу между весом и массой, так как в повседневной жизни слова «вес» и «масса» используются как синонимы.
 Вес – это сила, измеряемая в ньютонах или килограмм-силах, а не в килограммах. Если вы обсуждаете ваш «вес» с врачом, то вы обсуждаете вашу массу.
Вес – это сила, измеряемая в ньютонах или килограмм-силах, а не в килограммах. Если вы обсуждаете ваш «вес» с врачом, то вы обсуждаете вашу массу. - Ускорение свободного падения также может быть выражено в Н/кг. 1 Н/кг = 1 м/с 2 .
- Плечевые весы измеряют массу (в кг), в то время как весы, работа которых основана на сжатии или расширении пружины, измеряют вес (в кгс).
- Вес космонавта, который «весит» 101 кг (то есть его масса равна 101 кг), составляет 101,3 кгс на Северном полюсе и 16,5 кгс на Луне. На нейтронной звезде он будет весить еще больше, но он, вероятно, этого не заметит.
- Единица измерения «Ньютон» применяется намного чаще (чем удобная «кгс»), так как можно найти множество других величин, если сила измеряется в ньютонах.
Предупреждения Править
- Выражение «атомный вес» не имеет ничего общего с весом атома, это масса. В современной науке оно заменено на выражение «атомная масса».
Дополнительные статьи
найти область определения функции
переводить из двоичной системы в десятичную
найти квадратный корень числа вручную
перевести миллилитры в граммы
переводить из десятичной системы счисления в двоичную
Источник: http://ru. wikihow.com/%D0%B2%D1%8B%D1%87%D0%B8%D1%81%D0%BB%D0%B8%D1%82%D1%8C-%D0%B2%D0%B5%D1%81-%D1%87%D0%B5%D1%80%D0%B5%D0%B7-%D0%BC%D0%B0%D1%81%D1%81%D1%83
wikihow.com/%D0%B2%D1%8B%D1%87%D0%B8%D1%81%D0%BB%D0%B8%D1%82%D1%8C-%D0%B2%D0%B5%D1%81-%D1%87%D0%B5%D1%80%D0%B5%D0%B7-%D0%BC%D0%B0%D1%81%D1%81%D1%83
Формула веса
В обиходе и повседневной жизни понятия «масса» и «вес» абсолютно идентичны, хотя семантическое их значение принципиально разное. Спрашивая «Какой у тебя вес?» мы подразумеваем «Сколько в тебе килограммов?». Однако на вопрос, с помощью которого мы пытаемся выяснить этот факт, ответ дается не в килограммах, а в ньютонах. Придется вернуться к школьному курсе физики.
Вес тела — величина, характеризующая силу, с которой тело оказывает давление на опору или подвес.
Для сравнения, масса тела ранее грубо определялась как «количество вещества», современное определение звучит таким образом:
Масса — физическая величина, отражающая способность тела к инерции и являющаяся мерой его гравитационных свойств.
Понятие массы вообще несколько шире представленного здесь, однако наша задача состоит несколько в другом.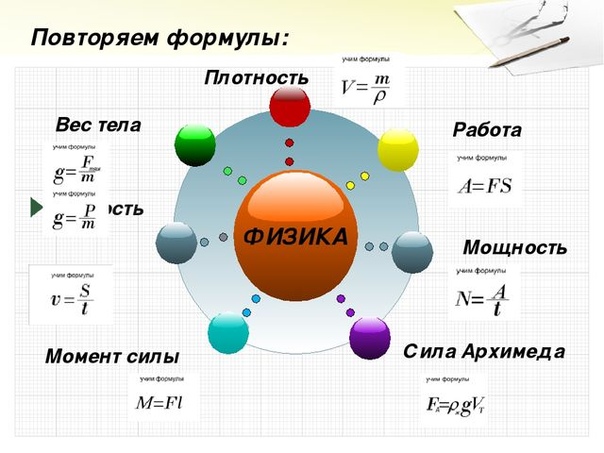 Вполне достаточно уяснить факт действительного различия между массой и весом.
Вполне достаточно уяснить факт действительного различия между массой и весом.
Кроме того, единица измерения массы — килограммы, а веса (как вида силы) — ньютоны.
И, пожалуй, самое главное отличие веса от массы содержит в себе сама формула веса, которая выглядит следующим образом:
где P — собственно вес тела (в Ньютонах), m — его масса в килограммах, а g — ускорение свободного падения, которое принято выражать в виде 9,8 Н/кг.
Иными словами, формула веса может быть понята на таком примере:
Гиря массой 1 кг подвешена к неподвижному динамометру, с тем, чтобы определить ее вес. Поскольку тело, да и сам динамометр, находятся в покое, то смело можно умножать его массу на ускорение свободного падения. Имеем: 1 (кг) х 9,8 (Н/кг)= 9,8 Н. Именно с такой силой действует гиря на подвес динамометра. Отсюда ясно, что вес тела равняется силе тяжести. Однако это не всегда так.
Самое время сделать важное замечание. Формула веса равняется силе формуле тяжести лишь в случаях, когда:
- тело находится в состояние покоя;
- на тело не действует сила Архимеда (выталкивающая сила).
 Любопытный факт, касающийся выталкивающей силы: известно, что тело, погруженное в воду, вытесняет объем воды, равный своем весу. Но оно не просто выталкивает воду, тело становится «легче» на объем вытесненной воды. Вот почему поднять в воде девушку массой 60 кг можно шутя и смеясь, а на поверхности это сделать куда сложнее.
Любопытный факт, касающийся выталкивающей силы: известно, что тело, погруженное в воду, вытесняет объем воды, равный своем весу. Но оно не просто выталкивает воду, тело становится «легче» на объем вытесненной воды. Вот почему поднять в воде девушку массой 60 кг можно шутя и смеясь, а на поверхности это сделать куда сложнее.
При неравномерном движении тела, т.е. когда тело совместно с подвесом движутся с ускорением a ,меняет свой облик и формула веса. Физика явления меняется незначительно, но в формуле такие изменения находят следующее отражение:
Как можно заменить по формуле, вес может быть отрицательным, но для этого ускорение, с которым движется тело, должно быть больше ускорения свободного падения. И тут опять важно отличать вес от массы: отрицательный вес не влияет на массу (свойства тела остаются те же), однако он фактически становится направлен в противоположную сторону.
Хорош пример с ускоренным лифтом: при его резком ускорении на непродолжительное время создается впечатление»притягивания к потолку». С таким ощущением, конечно, столкнуться достаточно просто. Гораздо сложнее прочувствовать состояние невесомости, которое в полной мере ощущают космонавты на орбите.
С таким ощущением, конечно, столкнуться достаточно просто. Гораздо сложнее прочувствовать состояние невесомости, которое в полной мере ощущают космонавты на орбите.
Невесомость — по сути, отсутствие веса. Для того чтобы такое было возможным, ускорение, с которым движется тело, должно быть равно пресловутому усорению g (9,8 Н/кг). Добиться такого эффекта проще всего на околоземной орбите. Гравитация, т.е. притяжение, по-прежнему действует на тело (спутник), однако она пренебрежимо мала. А ускорение дрейфующего по орбите спутника также стремится к нулю. Тут-то и возникает эффект отсутствия веса, поскольку тело вообще не соприкасается ни с опорой, ни с подвесом, а попросту парит в воздухе.
Частично с таким эффектом можно столкнуться при взлете самолета. На секунду возникает ощущение подвешенности в воздухе: в этот момент ускорение, с которым движется самолет, равно ускорению свободного падения.
Вновь возвращаясь к отличиям веса и массы, важно помнить, что формула веса тела отличается от формулы массы, которая выглядит как:
то есть плотность вещества, деленная на его объем.
Источник: http://fb.ru/article/37791/formula-vesa
Формула для измерения веса тела
Мы часто употребляем фразы наподобие: «Пачка конфет весит 250 грамм» или «я вешу 52 килограмма». Использование таких предложений происходит автоматический. Но что такое вес? Из чего он складывается и как его посчитать?
Для начала нужно понять, что неправильно говорить: «Этот предмет весит Х килограмм». В физике существует два разных понятия – масса и вес . Масса измеряется в килограммах, граммах, тонах и так далее, а вес тела рассчитывается в ньютонах. Поэтому, когда мы говорим, например, что мы весим 52 килограмма, мы на самом деле имеем в виду массу, а не вес.
Вес в физике
Масса – это мера инертности тела . Чем тело обладает большей инертностью, тем больше времени понадобится, чтобы придать ему скорость. Грубо говоря, чем выше значение массы, тем тяжелее сдвинуть предмет. В международной системе единиц массу измеряют в килограммах. Но её также измеряют и в других единицах, например;
Но её также измеряют и в других единицах, например;
Когда мы говорим один, два, три килограмма, мы сравниваем массу с эталонной массой (прообраз которой находится во Франции в МБМВ). Масса обозначается m.
Вес – это сила, которая действует на подвес или опору за счёт предмета, притягиваемого силой тяжести. Это векторная величина, а значит у него есть направление (как и у всех сил), в отличие от массы (скалярная величина). Направление всегда идёт в центр Земли (из-за силы тяжести). Например, если мы сидим на стуле, сиденье которого располагается параллельно Земле, то вектор силы направлен строго вниз. Вес обозначается P и рассчитывается в ньютонах [Н].
Если тело находится в движении или покое, то сила тяжести (Fтяж), действующая на тело, равна весу. Это справедливо, если движение происходит вдоль прямой линии относительно Земли, и оно имеет постоянную скорость. Вес действует на опору, а сила тяжести на само тело (которое располагается на опоре). Это разные величины, и независимо от того, что они равны в большинстве случаев, не стоит их путать.
Сила тяжести – это результат притяжения тела к земле, вес – воздействие тела на опору. Так как тело изгибает (деформирует) опору своим весом, возникает ещё одна сила, она называется сила упругости (Fупр). Третий закон Ньютона гласит, что тела взаимодействуют друг с другом с одинаковыми по модулю силами, но разными по вектору. Из этого следует, что для силы упругости должна быть противоположная сила, и эта она называется – сила реакции опоры и обозначается N.
По модулю |N|=|P|. Но так как эти силы разнонаправленные, то, раскрывая модуль, мы получим N= – P. Именно поэтому вес можно измерить динамометром, который состоит из пружинки и шкалы. Если подвесить груз на это устройство, пружинка растянется до определённой отметки на шкале.
Как измерить вес тела
Второй закон Ньютона гласит, что ускорение равно силе, делённой на массу. Таким образом, F=m*a. Так как Fтяж равна P (если тело находится в покое или движется по прямой (относительно Земли) с одинаковой скоростью), то и Р тела будет равняться произведению массы и ускорения (P=m*a).
Мы знаем, как найти массу, и знаем, что такое вес тела, осталось разобраться с ускорением. Ускорение – это физическая векторная величина, которая обозначает изменение скорости тела за единицу времени. Например, объект движется первую секунду со скоростью 4 м/с, а на второй секунде его скорость увеличивается до 8 м/с, значит, его ускорение равняется 2. По международной системе единиц ускорение рассчитывается в метрах на секунду в квадрате [м/с 2 ].
Если поместить тело в специальную среду, где будет отсутствовать сила сопротивления воздуха – вакуум, и убрать опору, то объект начнёт лететь равноускоренно. Название этого явления — ускорение свободного падения , которое обозначается g и рассчитывается в метрах на секунду в квадрате [м/с 2 ].
Интересно, что ускорение не зависит от массы тела, а значит если мы кинем листок бумажки и гирю на Земле в специальных условиях, при которых отсутствует воздух (вакуум), то эти предметы приземлятся в одно и то же время.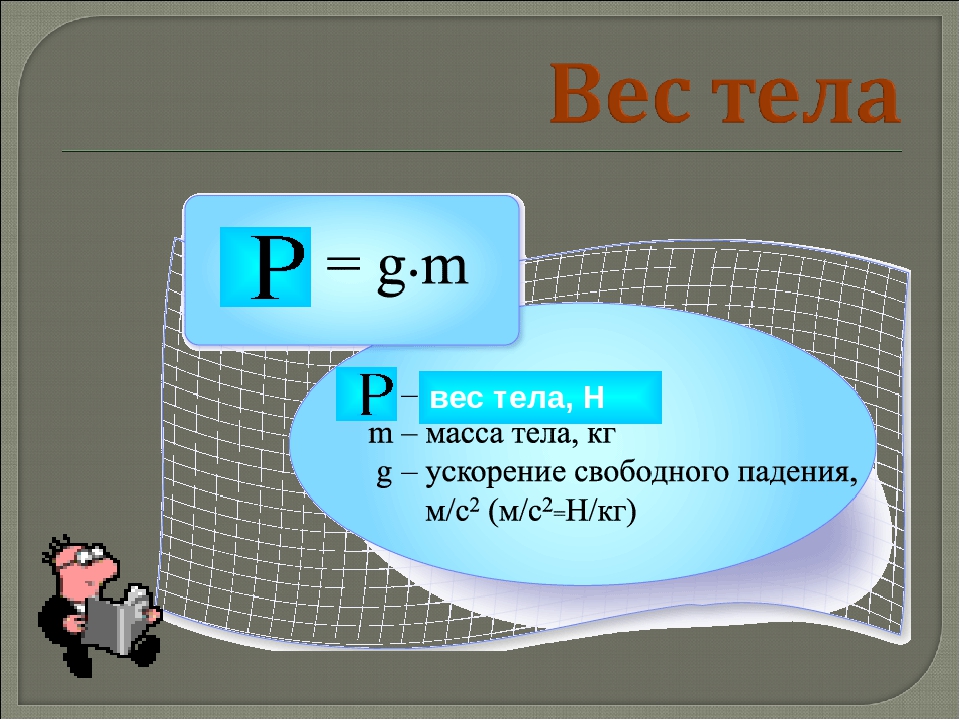 Так как листок имеет большую площадь поверхности и относительно маленькую массу, то для того чтобы упасть, ему приходятся сталкиваться с большим сопротивлением воздуха. В вакууме такого не происходит , и поэтому перо, листок бумаги, гиря, пушечное ядро и другие предметы будут лететь с одной и той же скоростью и упадут в одно время (при условии, что они начнут лететь в одно и то же время, и их первоначальная скорость будет равняться нулю).
Так как листок имеет большую площадь поверхности и относительно маленькую массу, то для того чтобы упасть, ему приходятся сталкиваться с большим сопротивлением воздуха. В вакууме такого не происходит , и поэтому перо, листок бумаги, гиря, пушечное ядро и другие предметы будут лететь с одной и той же скоростью и упадут в одно время (при условии, что они начнут лететь в одно и то же время, и их первоначальная скорость будет равняться нулю).
Так как Земля имеет форму геоида (или по-другому эллипсоида), а не идеального шара, то и ускорение свободного падения в разных участках Земли разное. Например, на экваторе оно равно 9,832 м/с 2 , а на полюсах 9,780 м/с 2 . Это происходит потому, что на некоторых участках Земли расстояние до ядра больше, а на некоторых меньше. Чем ближе объект находится к центру, тем сильнее он притягивается. Чем объект дальше, тем сила тяжести меньше. Обычно, в школе округляют это значение до 10, это делается для удобства расчётов. Если же необходимо измерить более точно (в инженерном или военном деле и так далее), то берут конкретные значения.
Таким образом, формула для расчёта веса телу будет выглядеть следующим образом P=m*g .
Примеры задач для расчёта веса тела
Первая задача . На стол положили груз массой 2 килограмма. Каков вес груза?
Для решения этой задачи нам понадобится формула по расчёту веса P=m*g. Мы знаем массу тела, а ускорение свободного падения примерно составляет 9,8 м/с 2 . Подставляем эти данные в формулу и получим P=2*9,8=19,6 Н. Ответ: 19,6 Н.
Вторая задача . На стол положили парафиновый шарик, объёмом 0,1 м 3 . Каков вес шарика?
Эту задачу необходимо решать в следующей последовательности;
- Для начала нам надо вспомнить формулу веса P=m*g. Ускорение нам известно – 9,8 м/с 2 . Осталось найти массу.
- Масса рассчитывается по формуле m=p*V, где p – это плотность, а V – объём. Плотность парафина можно посмотреть в таблице, объём нам известен.
- Необходимо подставить значения в формулу, для нахождения массы. m=900*0,1=90 кг.

- Теперь подставляем значения в первую формулу, для нахождения веса. P=90*9,9=882 Н.
В этом видео уроке разбирается тема – сила тяжести и вес тела.
Не получили ответ на свой вопрос? Предложите авторам тему.
Выпуск 15Пятнадцатая серия передачи посвящена новым физическим величинам — массе тела и его весу. Эти понятия часто путают и измеряют вес в килограммах. Но это является грубой ошибкой и профессор Даниил Эдисонович Кварк объяснит, почему это так. Можно ли изменить свой вес тела или даже сделать его совершенно невесомым? Физика отвечает утвердительно. Хотите узнать, как это сделать? Тогда смотрите видеоурок физики от Академии занимательных наук, посвящённый массе и весу тела.
Масса и вес тела
В чём заключается отличие между массой и весом тела? Вроде бы это одно и то же. Но почему тогда, стоя на весах, мы можем изменять их показания, выполняя те или иные действия (поднимая руки или сгибая туловище)? Видеоурок физики — это то, что нужно для выяснения этих вопросов. Да, разница есть. С точки зрения физики, неправильно интересоваться у продавца, сколько весит тот или иной продукт. А правильно — спросить, какова его масса! Вес это векторная величина, сила. Она всегда имеет направление. При неизменной массе тела, его вес можно изменить. Например, положив на весы банан и надавив на него рукой мы получим больший вес, в то время, как масса банана останется прежней. Вес тела — это сила, с которой это тело, притягиваясь к земле, давит на опору или растягивает подвес. Если масса тела измеряется в килограммах, то вес, как и любая сила — ньютонами. Теперь понятно, почему неверно говорить, что вес тела равен столько-то килограммам? Итак, вес тела всегда измеряется в ньютонах, в то время как масса тела может измерять в граммах, килограммах и т.д. В отличие от массы тела, вес тела не является постоянной величиной. Он может увеличиваться или уменьшаться, при этом масса тела останется прежней. Масса тела представляет собой скалярную величину. Почему если сильно раскачаться на качелях, начинает «захватывать дух»? Профессор Кварк считает, что это ощущение невесомости, похожее на то, которое бывает в космосе.
Да, разница есть. С точки зрения физики, неправильно интересоваться у продавца, сколько весит тот или иной продукт. А правильно — спросить, какова его масса! Вес это векторная величина, сила. Она всегда имеет направление. При неизменной массе тела, его вес можно изменить. Например, положив на весы банан и надавив на него рукой мы получим больший вес, в то время, как масса банана останется прежней. Вес тела — это сила, с которой это тело, притягиваясь к земле, давит на опору или растягивает подвес. Если масса тела измеряется в килограммах, то вес, как и любая сила — ньютонами. Теперь понятно, почему неверно говорить, что вес тела равен столько-то килограммам? Итак, вес тела всегда измеряется в ньютонах, в то время как масса тела может измерять в граммах, килограммах и т.д. В отличие от массы тела, вес тела не является постоянной величиной. Он может увеличиваться или уменьшаться, при этом масса тела останется прежней. Масса тела представляет собой скалярную величину. Почему если сильно раскачаться на качелях, начинает «захватывать дух»? Профессор Кварк считает, что это ощущение невесомости, похожее на то, которое бывает в космосе.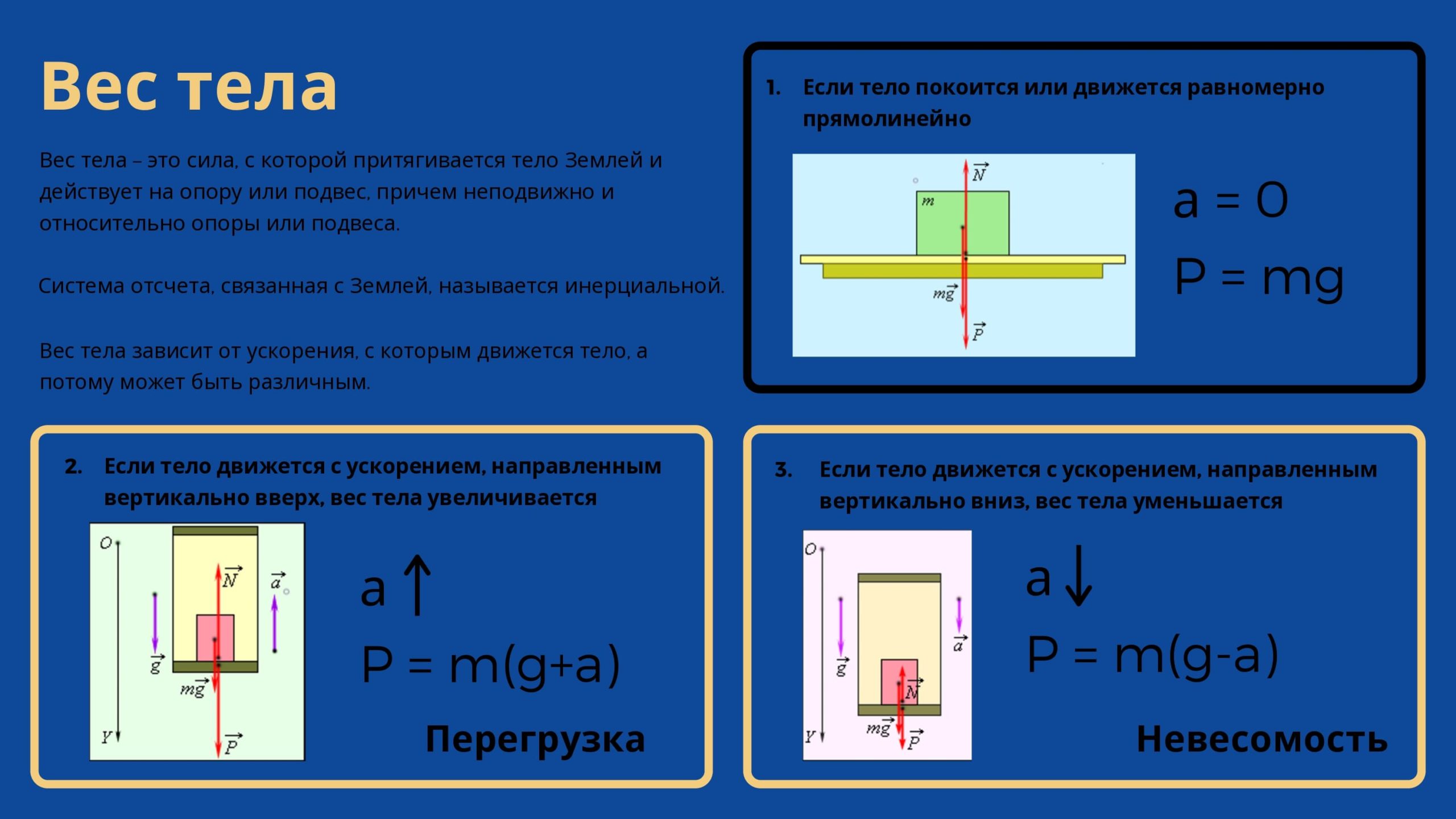 Как же получается, что вес тела становится равным нулю, пусть даже на какое-то мгновение? А получается так потому, что в момент падения тело ни на что не давит и ничего не оттягивает, следовательно, не имеет веса. Вот ещё один пример, доказывающий, что вес тела может меняться при неизменной массе. В воде все тела весят меньше, чем на суше. Иначе мы не могли бы плавать, а шли прямиком ко дну. Слон с массой тела в 1 тонну весит на суше больше, чем в воде. Киты с массой более 30 тонн способны в воде парить как птицы.
Как же получается, что вес тела становится равным нулю, пусть даже на какое-то мгновение? А получается так потому, что в момент падения тело ни на что не давит и ничего не оттягивает, следовательно, не имеет веса. Вот ещё один пример, доказывающий, что вес тела может меняться при неизменной массе. В воде все тела весят меньше, чем на суше. Иначе мы не могли бы плавать, а шли прямиком ко дну. Слон с массой тела в 1 тонну весит на суше больше, чем в воде. Киты с массой более 30 тонн способны в воде парить как птицы.
ВЕС ТЕЛА
сила, с к-рой тело действует вследствие тяготения к Земле на опору (или подвес), удерживающую его от свободного падения. Если тело и опора неподвижны относительно Земли, то В. т. равен его силе тяжести. Единица В. т. (в СИ) — ньютон (Н).
Большой энциклопедический политехнический словарь . 2004 .
Смотреть что такое «ВЕС ТЕЛА» в других словарях:
вес тела — Модуль равнодействующей сил тяжести, действующих на частицы этого тела. [Сборник рекомендуемых терминов. Выпуск 102. Теоретическая механика. Академия наук СССР. Комитет научно технической терминологии. 1984 г.] Тематики теоретическая механика… … Справочник технического переводчика
[Сборник рекомендуемых терминов. Выпуск 102. Теоретическая механика. Академия наук СССР. Комитет научно технической терминологии. 1984 г.] Тематики теоретическая механика… … Справочник технического переводчика
вес тела — Модуль равнодействующей сил тяжести, действующих на частицы этого тела … Политехнический терминологический толковый словарь
См. Масса тела человека. * * * ВЕС ТЕЛА ЧЕЛОВЕКА ВЕС ТЕЛА ЧЕЛОВЕКА, см. Масса тела человека (см. МАССА ТЕЛА ЧЕЛОВЕКА) … Энциклопедический словарь
См. Масса тела человека … Большой Энциклопедический словарь
См. Масса тела человека … Большая советская энциклопедия
То же, что масса тела человека … Естествознание. Энциклопедический словарь
ПОНИЖЕННЫЙ ВЕС ТЕЛА — Вообще – состояние, при котором вес тела 10% или более ниже нормы для типа институции человека и его возраста. Как и ожирение, этот термин используется довольно свободно, так как невозможно дать определение, которое в равной степени относится ко… … Толковый словарь по психологии
Вес: В физике: Вес сила воздействия тела на опору или подвес. Удельный вес отношение веса вещества к его объёму. Статистический вес, в квантовой механике и квантовой статистике число различных квантовых состояний с данной… … Википедия
Удельный вес отношение веса вещества к его объёму. Статистический вес, в квантовой механике и квантовой статистике число различных квантовых состояний с данной… … Википедия
ВЕС, сила ГРАВИТАЦИОННОГО притяжения тела. Вес тела равен произведению массы тела на ускорение свободного падения. Масса остается постоянной, но вес зависит от расположения объекта на поверхности Земли. С увеличением высоты вес уменьшается … Научно-технический энциклопедический словарь
Сущ., м., употр. часто Морфология: (нет) чего? веса и весу, чему? весу, (вижу) что? вес, чем? весом, о чём? о весе; мн. что? веса, (нет) чего? весов, чему? весам, (вижу) что? веса, чем? весами, о чём? о весах 1. Вес какого либо физического… … Толковый словарь Дмитриева
Книги
- Весёлая энциклопедия для девочек и мальчиков. 300 вопросов , Скиба Тамара Викторовна. Любые родители мечтают найти книгу, которая в простой и увлекательной форме давала бы ответы на бесконечные вопросы маленьких почемучек.
 Детей интересует буквально всё:-Куда пропадает Солнце…
Детей интересует буквально всё:-Куда пропадает Солнце… - Весёлая анатомия. Формирование представлений о себе и о своем теле , Нищев Валерий Михайлович. Наглядно-дидактическое пособие с красочными рисунками и забавными стихотворениями поможет сформировать у дошкольников представления о строении своего тела, об элементарных правилах гигиены и…
Вес тела проявление. Базовая физика
Понятие, с которым мы знакомы с самого раннего детства, — масса. И все же в курсе физики с ее изучением связаны некоторые трудности. Поэтому нужно четко определить, Как ее можно узнать? И почему она не равна весу?
Определение массы
Естественнонаучный смысл этой величины в том, что она определяет количество вещества, которое содержится в теле. Для ее обозначения принято использовать латинскую букву m. Единицей измерения в стандартной системе является килограмм. В задачах и повседневной жизни часто используются и внесистемные: грамм и тонна.
В школьном курсе физики ответ на вопрос: «Что такое масса?» дается при изучении явления инерции.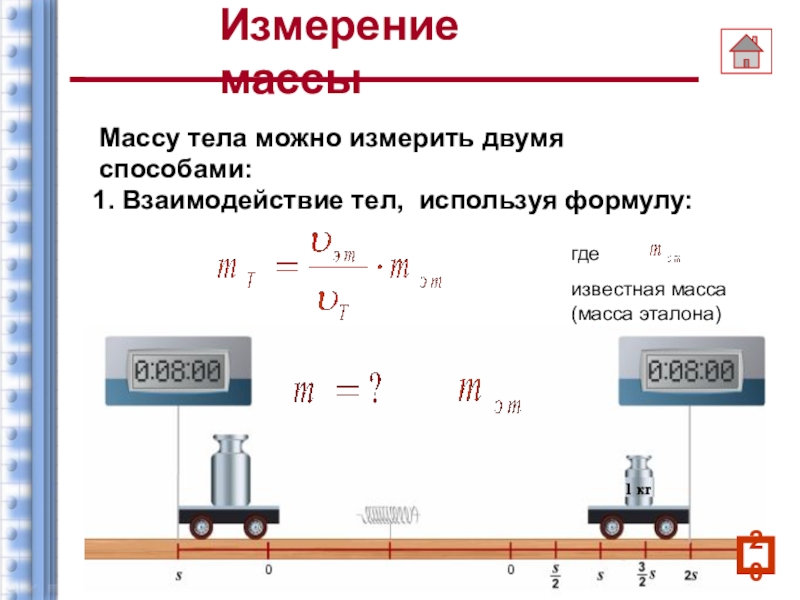 Тогда она определяется, как способность тела сопротивляться изменению скорости своего движения. Поэтому массу еще называют инертной.
Тогда она определяется, как способность тела сопротивляться изменению скорости своего движения. Поэтому массу еще называют инертной.
Что такое вес?
Во-первых, это сила, то есть вектор. Масса же является скалярной веса всегда приложен к опоре или подвесу и направлен в ту же сторону, что и сила тяжести, то есть вертикально вниз.
Формула для вычисления веса зависит от того, движется ли эта опора (подвес). В случае покоя системы используется такое выражение:
Р = m * g, где Р (в английских источниках используется буква W) — вес тела, g — ускорение свободного падения. Для земли g принято брать равным 9,8 м/с 2 .
Из нее может быть выведена формула массы: m = Р / g.
При движении вниз, то есть в направлении действия веса, его значение уменьшается. Поэтому формула принимает вид:
Р = m (g — а). Здесь «а» — это ускорение движения системы.
То есть при равенстве этих двух ускорений наблюдается состояние невесомости, когда вес тела равен нулю.
Когда тело начинает двигаться вверх, то говорят об увеличении веса. В этой ситуации возникает состояние перегрузки. Потому что вес тела увеличивается, а формула его будет выглядеть так:
Р = m (g + а).
Как масса связана с плотностью?
Решение. 800 кг/м 3 . Для того чтобы воспользоваться уже известной формулой, нужно знать объем пятна. Его легко вычислить, если принять пятно за цилиндр. Тогда формула объема будет такой:
V = π * r 2 * h.
Причем r — это радиус, а h — высота цилиндра. Тогда объем получится равным 668794,88 м 3 . Теперь можно сосчитать массу. Она получится такой: 535034904 кг.
Ответ: масса нефти приблизительно равна 535036 т.
Задача № 5. Условие: Длина самого длинного телефонного кабеля равна 15151 км. Чему равна масса меди, которая пошла на его изготовление, если сечение проводов равно 7,3 см 2 ?
Решение. Плотность меди равна 8900 кг/м 3 . Объем находится по формуле, которая содержит произведение площади основания на высоту (здесь длину кабеля) цилиндра. Но сначала нужно перевести эту площадь в квадратные метры. То есть разделить данное число на 10000. После расчетов получается, что объем всего кабеля приблизительно равен 11000 м 3 .
Но сначала нужно перевести эту площадь в квадратные метры. То есть разделить данное число на 10000. После расчетов получается, что объем всего кабеля приблизительно равен 11000 м 3 .
Теперь нужно перемножить значения плотности и объема, чтобы узнать, чему равна масса. Результатом оказывается число 97900000 кг.
Ответ: масса меди равна 97900 т.
Еще одна задача, связанная с массой
Задача № 6. Условие: Самая большая свеча массой 89867 кг была диаметром 2,59 м. Какой была ее высота?
Решение. Плотность воска — 700 кг/м 3 . Высоту потребуется найти из То есть V нужно разделить на произведение π и квадрата радиуса.
А сам объем вычисляется по массе и плотности. Он оказывается равным 128,38 м 3 . Высота же составила 24,38 м.
Ответ: высота свечи равна 24,38 м.
Назад
Вперёд
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Данная презентация предназначена в помощь учащимся 9-10 классов при подготовке темы «Вес тела».
Цели презентации:
- Повторить и углубить понятия: «сила тяжести»; «вес тела»; «невесомость».
- Акцентировать внимание учащихся на то, что сила тяжести и вес тела – разные силы.
- Научить учащихся определять вес тела, движущегося по вертикали.
В повседневной жизни массу тела определяют взвешиванием. Из курса физики 7 класса известно, что сила тяжести прямо пропорциональна массе тела. Поэтому вес тела часто отождествляют с его массой или силой тяжести. С точки зрения физики – это грубейшая ошибка. Вес тела – это сила, но сила тяжести и вес тела – разные силы.
Сила тяжести – частный случай проявления сил всемирного тяготения. Поэтому уместно вспомнить закон всемирного тяготения, а также то, что силы гравитационного притяжения проявляются тогда, когда тела или одно из тел имеют огромные массы (слайд 2).
При применении закона всемирного тяготения для земных условий (слайд 3) планету можно рассматривать как однородный шар, а небольшие тела вблизи ее поверхности как точечные массы. Радиус земли равен 6400 км. Масса Земли равна 6∙10 24 кг.
= ,
где g – ускорение свободного падения.
Вблизи поверхности Земли g = 9,8 м/c 2 ≈ 10 м/c 2 .
Вес тела – сила, с которой это тело действует на горизонтальную опору или растягивает подвес.
Рис.1
На рис. 1 показано тело на опоре. Сила реакции опоры N (F упр) приложена не к опоре, а к находящемуся на ней телу. Модуль силы реакции опоры равен модулю веса по третьему закону Ньютона. Вес тела – частный случай проявления силы упругости. Важнейшей особенностью веса является то, что его значение зависит от ускорения, с которым движется опора или подвес. Вес равен силе тяжести только для покоящегося тела (или тела, движущегося с постоянной скоростью). Если же тело движется с ускорением, то вес может быть и больше, и меньше силы тяжести, и даже равным нулю.
В презентации на примере решения задачи 1 рассматриваются различные случаи определения веса груза массой 500 г, подвешенного к пружине динамометра, в зависимости от характера движения:
а) груз поднимают вверх с ускорением 2 м/c 2 ;
б) груз опускают вниз с ускорением 2 м/c 2 ;
в) груз равномерно поднимают вверх;
г) груз свободно падает.
Задания на расчет веса тела входят в раздел «Динамика». Решение задач на динамику основывается на использовании законов Ньютона с последующим проецированием на выбранные оси координат. Этим определяется последовательность действий.
- Выполняют чертеж, на котором изображают силы, действующие на тело (тела), и направление ускорения. Если направление ускорения неизвестно, его выбирают произвольно, а решение задачи дает ответ о правильности выбора.
- Записывают второй закон Ньютона в векторном виде.
- Выбирают оси. Обычно одну из осей удобно направить вдоль направления ускорения тела, вторую – перпендикулярно ускорению.
 Выбор осей определяется соображениями удобства: так, чтобы выражения для проекций законов Ньютона имели бы наиболее простой вид.
Выбор осей определяется соображениями удобства: так, чтобы выражения для проекций законов Ньютона имели бы наиболее простой вид. - Полученные в проекциях на оси векторные уравнения дополняют соотношениями, вытекающими из текста условий задачи. Например, уравнениями кинематической связи, определениями физических величин, третьим законом Ньютона.
- Используя полученную систему уравнений, пытаются дать ответ на вопрос задачи.
Настройка анимации в презентации позволяет сделать акцент на последовательность действий при решении задач. Это важно, так как навыки, приобретенные при решении задач на расчет веса тела, пригодятся учащимся при изучении других тем и разделов физики.
Решение задачи 1.
1а. Тело движется с ускорением 2 м/c 2 вверх (слайд 7).
Рис.2
1б. Тело движется с ускорением вниз (слайд 8). Ось OY направляем вниз, тогда проекции сил тяжести и упругости в уравнении (2) меняют знаки, и оно имеет вид:
(2) mg – F упр = ma.
Следовательно, Р = m(g-a) = 0,5 кг∙(10 м/c 2 — 2 м/c 2) = 4 Н.
1в. При равномерном движении (слайд 9) уравнение (2) имеет вид:
(2) mg – F упр = 0, т. к. ускорение отсутствует.
Следовательно, Р = mg = 5 Н.
1г. При свободном падении = (слайд 10). Воспользуемся результатом решения задачи 1б:
P = m(g – a) = 0,5 кг(10 м/c 2 – 10 м/c 2) = 0 H.
Состояние, при котором вес тела равен нулю, называют состоянием невесомости.
На тело действует только сила тяжести.
Говоря о невесомости, следует отметить, что длительное состояние невесомости испытывают космонавты во время полета при выключенных двигателях космического
корабля, а чтобы испытать кратковременное состояние невесомости, достаточно просто подпрыгнуть. Бегущий человек в момент, когда его ноги не касаются земли, тоже находится в состоянии невесомости.
Презентация может быть использована на уроке при объяснении темы «Вес тела».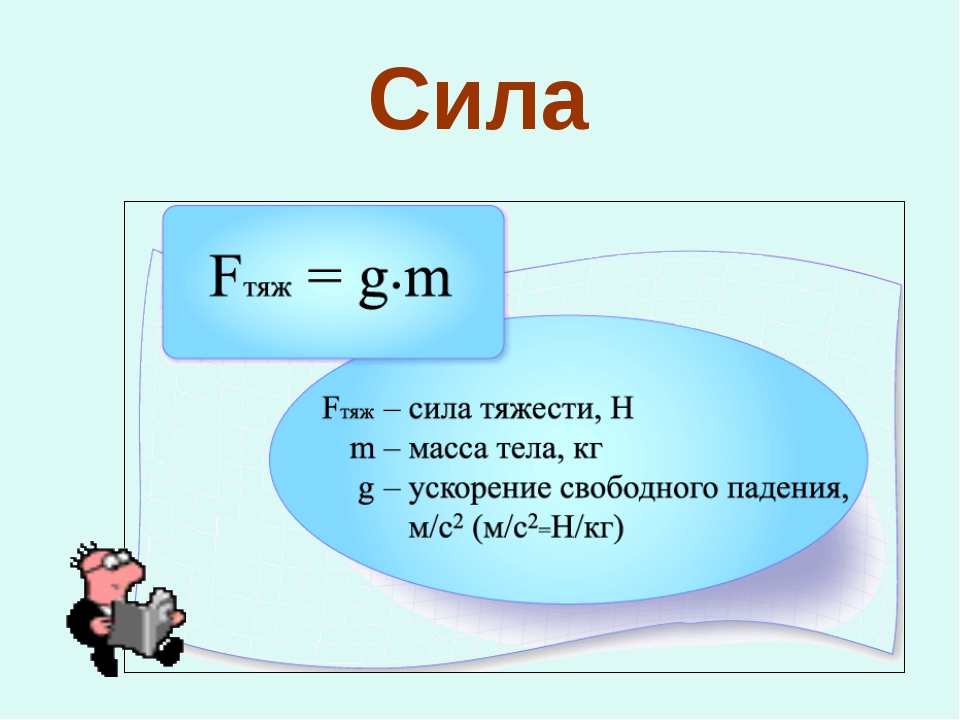 В зависимости от уровня подготовки класса учащимся могут быть предложены не все слайды с решениями задачи 1. Например, в классах с повышенной мотивацией к изучению физики достаточно объяснить, как рассчитать вес тела, движущегося с ускорением вверх (задача 1а), а остальные задачи (б, в, г) предоставить для самостоятельного решения с последующей проверкой. Выводы, полученные в результате решения задачи1, ученики должны попытаться сделать самостоятельно.
В зависимости от уровня подготовки класса учащимся могут быть предложены не все слайды с решениями задачи 1. Например, в классах с повышенной мотивацией к изучению физики достаточно объяснить, как рассчитать вес тела, движущегося с ускорением вверх (задача 1а), а остальные задачи (б, в, г) предоставить для самостоятельного решения с последующей проверкой. Выводы, полученные в результате решения задачи1, ученики должны попытаться сделать самостоятельно.
Выводы (слайд 11).
- Вес тела и сила тяжести – разные силы. У них разная природа. Эти силы приложены к разным телам: сила тяжести — к телу; вес тела — к опоре (подвесу).
- Вес тела совпадает с силой тяжести только тогда, когда тело неподвижно или движется равномерно и прямолинейно, и другие силы, кроме силы тяжести и реакции опоры (натяжение подвеса), на него не действуют.
- Вес тела больше силы тяжести (Р > mg), если ускорение тела направлено в сторону, противоположную направлению силы тяжести.
- Вес тела меньше силы тяжести (Р
- Состояние, при котором вес тела равен нулю, называют состоянием невесомости.
 Тело находится в состоянии невесомости, когда оно движется с ускорением свободного падения, то есть когда на него действует только сила тяжести.
Тело находится в состоянии невесомости, когда оно движется с ускорением свободного падения, то есть когда на него действует только сила тяжести.
Задачи 2 и 3 (слайд 12) могут быть предложены учащимся в качестве домашнего задания.
Презентация «Вес тела» может быть использована для дистанционного обучения. В этом случае рекомендуется:
- при просмотре презентации решение задачи 1 записать в тетрадь;
- самостоятельно решить задачи 2, 3, применяя предложенную в презентации последовательность действий.
Презентация по теме «Вес тела» позволяет показать теорию решения задач на динамику в интересной, доступной трактовке. Презентация активирует познавательную деятельность учащихся и позволяет формировать правильный подход к решению физических задач.
Литература:
- Гринченко Б.И. Физика 10-11. Теория решения задач. Для старшеклассников и поступающих в вузы. – Великие Луки: Великолукская городская типография, 2005.
- Генденштейн Л.
 Э. Физика. 10 класс. В 2 ч. Ч 1./Л.Э. Генденштейн, Ю.И. Дик. – М.: Мнемозина, 2009.
Э. Физика. 10 класс. В 2 ч. Ч 1./Л.Э. Генденштейн, Ю.И. Дик. – М.: Мнемозина, 2009. - Генденштейн Л.Э. Физика. 10 класс. В 2 ч. Ч 2. Задачник./Л.Э. Генденштейн, Л.А. Кирик, И.М. Гельгафгат, И.Ю. Ненашев.- М.: Мнемозина, 2009.
Интернет-ресурсы:
- images.yandex.ru
- videocat.chat.ru
Мы часто употребляем фразы наподобие: «Пачка конфет весит 250 грамм» или «я вешу 52 килограмма». Использование таких предложений происходит автоматический. Но что такое вес? Из чего он складывается и как его посчитать?
Для начала нужно понять, что неправильно говорить: «Этот предмет весит Х килограмм». В физике существует два разных понятия – масса и вес . Масса измеряется в килограммах, граммах, тонах и так далее, а вес тела рассчитывается в ньютонах. Поэтому, когда мы говорим, например, что мы весим 52 килограмма, мы на самом деле имеем в виду массу, а не вес.
Масса – это мера инертности тела . Чем тело обладает большей инертностью, тем больше времени понадобится, чтобы придать ему скорость. Грубо говоря, чем выше значение массы, тем тяжелее сдвинуть предмет. В международной системе единиц массу измеряют в килограммах. Но её также измеряют и в других единицах, например;
Грубо говоря, чем выше значение массы, тем тяжелее сдвинуть предмет. В международной системе единиц массу измеряют в килограммах. Но её также измеряют и в других единицах, например;
- унция;
- фунт;
- стоун;
- американская тонна;
- английская тонна;
- грамм;
- миллиграмм и так далее.
Когда мы говорим один, два, три килограмма, мы сравниваем массу с эталонной массой (прообраз которой находится во Франции в МБМВ). Масса обозначается m.
Вес – это сила, которая действует на подвес или опору за счёт предмета, притягиваемого силой тяжести. Это векторная величина, а значит у него есть направление (как и у всех сил), в отличие от массы (скалярная величина). Направление всегда идёт в центр Земли (из-за силы тяжести). Например, если мы сидим на стуле, сиденье которого располагается параллельно Земле, то вектор силы направлен строго вниз. Вес обозначается P и рассчитывается в ньютонах [Н].
Если тело находится в движении или покое, то сила тяжести (Fтяж), действующая на тело, равна весу. Это справедливо, если движение происходит вдоль прямой линии относительно Земли, и оно имеет постоянную скорость. Вес действует на опору, а сила тяжести на само тело (которое располагается на опоре). Это разные величины, и независимо от того, что они равны в большинстве случаев, не стоит их путать.
Это справедливо, если движение происходит вдоль прямой линии относительно Земли, и оно имеет постоянную скорость. Вес действует на опору, а сила тяжести на само тело (которое располагается на опоре). Это разные величины, и независимо от того, что они равны в большинстве случаев, не стоит их путать.
Сила тяжести – это результат притяжения тела к земле, вес – воздействие тела на опору. Так как тело изгибает (деформирует) опору своим весом, возникает ещё одна сила, она называется сила упругости (Fупр). Третий закон Ньютона гласит, что тела взаимодействуют друг с другом с одинаковыми по модулю силами, но разными по вектору. Из этого следует, что для силы упругости должна быть противоположная сила, и эта она называется – сила реакции опоры и обозначается N.
По модулю |N|=|P|. Но так как эти силы разнонаправленные, то, раскрывая модуль, мы получим N= — P. Именно поэтому вес можно измерить динамометром, который состоит из пружинки и шкалы. Если подвесить груз на это устройство, пружинка растянется до определённой отметки на шкале.
Как измерить вес тела
Второй закон Ньютона гласит, что ускорение равно силе, делённой на массу. Таким образом, F=m*a. Так как Fтяж равна P (если тело находится в покое или движется по прямой (относительно Земли) с одинаковой скоростью), то и Р тела будет равняться произведению массы и ускорения (P=m*a).
Мы знаем, как найти массу, и знаем, что такое вес тела, осталось разобраться с ускорением. Ускорение – это физическая векторная величина, которая обозначает изменение скорости тела за единицу времени. Например, объект движется первую секунду со скоростью 4 м/с, а на второй секунде его скорость увеличивается до 8 м/с, значит, его ускорение равняется 2. По международной системе единиц ускорение рассчитывается в метрах на секунду в квадрате [м/с 2 ].
Если поместить тело в специальную среду, где будет отсутствовать сила сопротивления воздуха – вакуум, и убрать опору, то объект начнёт лететь равноускоренно. Название этого явления — ускорение свободного падения , которое обозначается g и рассчитывается в метрах на секунду в квадрате [м/с 2 ].
Интересно, что ускорение не зависит от массы тела, а значит если мы кинем листок бумажки и гирю на Земле в специальных условиях, при которых отсутствует воздух (вакуум), то эти предметы приземлятся в одно и то же время. Так как листок имеет большую площадь поверхности и относительно маленькую массу, то для того чтобы упасть, ему приходятся сталкиваться с большим сопротивлением воздуха. В вакууме такого не происходит , и поэтому перо, листок бумаги, гиря, пушечное ядро и другие предметы будут лететь с одной и той же скоростью и упадут в одно время (при условии, что они начнут лететь в одно и то же время, и их первоначальная скорость будет равняться нулю).
Так как Земля имеет форму геоида (или по-другому эллипсоида), а не идеального шара, то и ускорение свободного падения в разных участках Земли разное. Например, на экваторе оно равно 9,832 м/с 2 , а на полюсах 9,780 м/с 2 . Это происходит потому, что на некоторых участках Земли расстояние до ядра больше, а на некоторых меньше. Чем ближе объект находится к центру, тем сильнее он притягивается. Чем объект дальше, тем сила тяжести меньше. Обычно, в школе округляют это значение до 10, это делается для удобства расчётов. Если же необходимо измерить более точно (в инженерном или военном деле и так далее), то берут конкретные значения.
Чем ближе объект находится к центру, тем сильнее он притягивается. Чем объект дальше, тем сила тяжести меньше. Обычно, в школе округляют это значение до 10, это делается для удобства расчётов. Если же необходимо измерить более точно (в инженерном или военном деле и так далее), то берут конкретные значения.
Таким образом, формула для расчёта веса телу будет выглядеть следующим образом P=m*g .
Примеры задач для расчёта веса тела
Первая задача . На стол положили груз массой 2 килограмма. Каков вес груза?
Для решения этой задачи нам понадобится формула по расчёту веса P=m*g. Мы знаем массу тела, а ускорение свободного падения примерно составляет 9,8 м/с 2 . Подставляем эти данные в формулу и получим P=2*9,8=19,6 Н. Ответ: 19,6 Н.
Вторая задача . На стол положили парафиновый шарик, объёмом 0,1 м 3 . Каков вес шарика?
Эту задачу необходимо решать в следующей последовательности;
- Для начала нам надо вспомнить формулу веса P=m*g.
 Ускорение нам известно – 9,8 м/с 2 . Осталось найти массу.
Ускорение нам известно – 9,8 м/с 2 . Осталось найти массу. - Масса рассчитывается по формуле m=p*V, где p – это плотность, а V – объём. Плотность парафина можно посмотреть в таблице, объём нам известен.
- Необходимо подставить значения в формулу, для нахождения массы. m=900*0,1=90 кг.
- Теперь подставляем значения в первую формулу, для нахождения веса. P=90*9,9=882 Н.
Ответ: 882 Н.
Видео
В этом видео уроке разбирается тема — сила тяжести и вес тела.
Не получили ответ на свой вопрос? Предложите авторам тему.
Какое слово вы употребляете чаще: «масса» или «вес»? Думаю, это зависит от вашей профессии. Если вы учитель физики, то слово «масса» встречается в вашей речи чаще. Если же вы продавец в магазине, то слово «вес» вы слышите и произносите много раз в день. В чём же отличия массы от веса и причём тут профессиональная деятельность? Масса и вес – синонимы, но не абсолютные. Для начала, у обоих слов существует несколько значений. В этом легко убедиться на примере таких словосочетаний: «вес твоего голоса», «вес груза», «масса отличий», «масса тела». Основные значения этих слов в обиходе совпадают, но в науке, особенно в физике, отличия между массой и весом значительные. Так, масса – это физическая величина, определяющая инертные и гравитационные свойства тел. Масса определяет количество вещества в предмете. Вес – это сила, с которой объект давит на опору, чтобы не упасть. Исходя из этого определения, приходим к выводу, что в случае с весом гравитационная составляющая является обязательной для дачи верного определения. Так, например, если вес космонавта на земле 80 кг, то его вес на орбите будет почти нулевой, на Луне он бы весил меньше 15 кг, а вот на Юпитере — почти 200 кг. При этом его масса во всех случаях остается неизменной.
В этом легко убедиться на примере таких словосочетаний: «вес твоего голоса», «вес груза», «масса отличий», «масса тела». Основные значения этих слов в обиходе совпадают, но в науке, особенно в физике, отличия между массой и весом значительные. Так, масса – это физическая величина, определяющая инертные и гравитационные свойства тел. Масса определяет количество вещества в предмете. Вес – это сила, с которой объект давит на опору, чтобы не упасть. Исходя из этого определения, приходим к выводу, что в случае с весом гравитационная составляющая является обязательной для дачи верного определения. Так, например, если вес космонавта на земле 80 кг, то его вес на орбите будет почти нулевой, на Луне он бы весил меньше 15 кг, а вот на Юпитере — почти 200 кг. При этом его масса во всех случаях остается неизменной.
Официально масса и вес имеют различные единицы измерения, масса – килограммы, вес – ньютоны. Интересно, что в медицине традиционно мы имеем дело с понятием «вес человека», «вес новорождённого», который измеряют в килограммах, то есть на самом деле речь идёт о массе. При этом масса не подразумевает действие каких-либо сил, как вес. Это величина, которая рассчитывается в состоянии покоя и инертности.
При этом масса не подразумевает действие каких-либо сил, как вес. Это величина, которая рассчитывается в состоянии покоя и инертности.
Выводы сайт
- Масса — фундаментальная физическая величина, определяющая количество вещества и инертные свойства тела. Вес — это сила, с которой предмет давит на опору, которая зависит от гравитации. Например, масса человека на разных планетах остается той же, а вес меняется в зависимости от силы тяжести.
- Масса стандартно измеряется в килограммах, вес – в ньютонах.
В обиходе и повседневной жизни понятия «масса» и «вес» абсолютно идентичны, хотя семантическое их значение принципиально разное. Спрашивая «Какой у тебя вес?» мы подразумеваем «Сколько в тебе килограммов?». Однако на вопрос, с помощью которого мы пытаемся выяснить этот факт, ответ дается не в килограммах, а в ньютонах. Придется вернуться к школьному курсе физики.
Вес тела — величина, характеризующая силу, с которой тело оказывает давление на опору или подвес.
Для сравнения, масса тела ранее грубо определялась как «количество вещества», современное определение звучит таким образом:
Масса — физическая величина, отражающая способность тела к инерции и являющаяся мерой его гравитационных свойств.
Понятие массы вообще несколько шире представленного здесь, однако наша задача состоит несколько в другом. Вполне достаточно уяснить факт действительного различия между массой и весом.
Кроме того, — килограммы, а веса (как вида силы) — ньютоны.
И, пожалуй, самое главное отличие веса от массы содержит в себе сама формула веса, которая выглядит следующим образом:
где P — собственно вес тела (в Ньютонах), m — его масса в килограммах, а g — ускорение которое принято выражать в виде 9,8 Н/кг.
Иными словами, формула веса может быть понята на таком примере:
Гиря массой 1 кг подвешена к неподвижному динамометру, с тем, чтобы определить ее вес. Поскольку тело, да и сам динамометр, находятся в покое, то смело можно умножать его массу на ускорение свободного падения. Имеем: 1 (кг) х 9,8 (Н/кг)= 9,8 Н. Именно с такой силой действует гиря на подвес динамометра. Отсюда ясно, что вес тела равняется Однако это не всегда так.
Имеем: 1 (кг) х 9,8 (Н/кг)= 9,8 Н. Именно с такой силой действует гиря на подвес динамометра. Отсюда ясно, что вес тела равняется Однако это не всегда так.
Самое время сделать важное замечание. Формула веса равняется тяжести лишь в случаях, когда:
- тело находится в состояние покоя;
- на тело не действует сила Архимеда (выталкивающая сила). Любопытный факт, касающийся известно, что тело, погруженное в воду, вытесняет объем воды, равный своем весу. Но оно не просто выталкивает воду, тело становится «легче» на объем вытесненной воды. Вот почему поднять в воде девушку массой 60 кг можно шутя и смеясь, а на поверхности это сделать куда сложнее.
При неравномерном движении тела, т.е. когда тело совместно с подвесом движутся с ускорением a ,меняет свой облик и формула веса. Физика явления меняется незначительно, но в формуле такие изменения находят следующее отражение:
P=m (g-a).
Как можно заменить по формуле, вес может быть отрицательным, но для этого ускорение, с которым движется тело, должно быть больше ускорения свободного падения.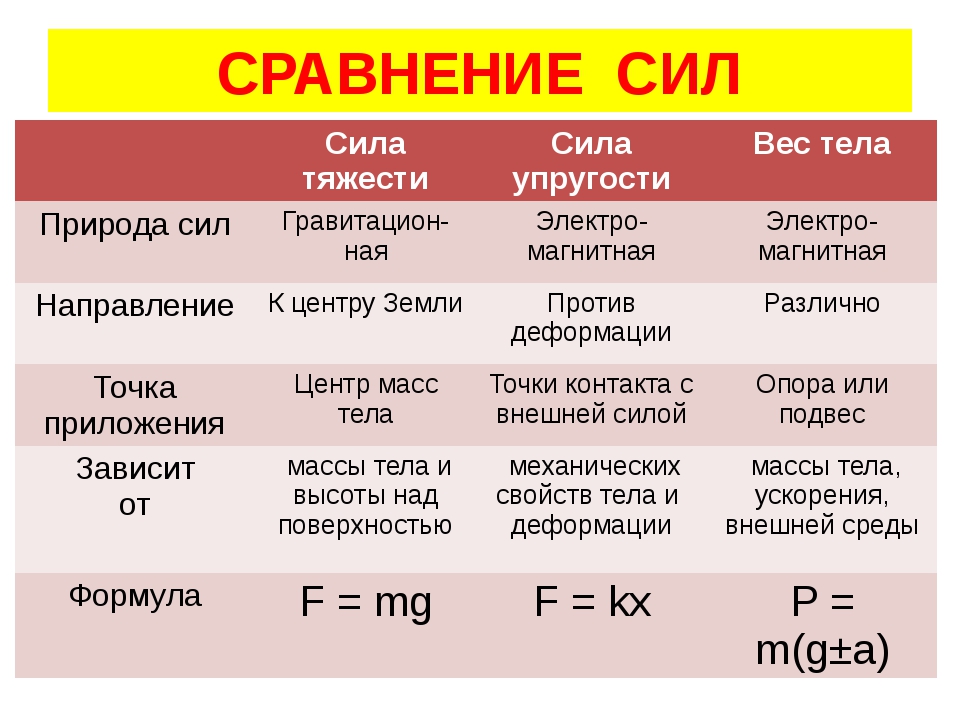 И тут опять важно отличать вес от массы: отрицательный вес не влияет на массу (свойства тела остаются те же), однако он фактически становится направлен в противоположную сторону.
И тут опять важно отличать вес от массы: отрицательный вес не влияет на массу (свойства тела остаются те же), однако он фактически становится направлен в противоположную сторону.
Хорош пример с ускоренным лифтом: при его резком ускорении на непродолжительное время создается впечатление»притягивания к потолку». С таким ощущением, конечно, столкнуться достаточно просто. Гораздо сложнее прочувствовать состояние невесомости, которое в полной мере ощущают космонавты на орбите.
Невесомость — по сути, отсутствие веса. Для того чтобы такое было возможным, ускорение, с которым движется тело, должно быть равно пресловутому усорению g (9,8 Н/кг). Добиться такого эффекта проще всего на околоземной орбите. Гравитация, т.е. притяжение, по-прежнему действует на тело (спутник), однако она пренебрежимо мала. А ускорение дрейфующего по орбите спутника также стремится к нулю. Тут-то и возникает эффект отсутствия веса, поскольку тело вообще не соприкасается ни с опорой, ни с подвесом, а попросту парит в воздухе.
Частично с таким эффектом можно столкнуться при взлете самолета. На секунду возникает ощущение подвешенности в воздухе: в этот момент ускорение, с которым движется самолет, равно ускорению свободного падения.
Вновь возвращаясь к отличиям веса и массы, важно помнить, что формула веса тела отличается от формулы массы, которая выглядит как:
m=ρ/V,
то есть плотность вещества, деленная на его объем.
Рекомендуем также
Вес тела в физике. Невесомость и перегрузка
Вес , как и любая другая сила, в системе СИ измеряется в Ньютонах.
Следы на снегу или на песке свидетельствуют о том, что человек или животное, проходя, давит на снежную или песчаную опору с некоторой силой.
Вес тела во время движения. Состояния невесомости и перегрузки
Вес тела зависит от ускорения, с которым движется тело, а потому может быть различным:
- Если тело покоится или движется равномерно прямолинейно, т.
 е. ускорение тела равно нулю, вес тела равен силе тяжести.
е. ускорение тела равно нулю, вес тела равен силе тяжести.
По второму закону Ньютона:
или в проекции на ось :
откуда
По третьему закону Ньютона:
- Если тело движется с ускорением, направленным вертикально вверх, вес тела увеличивается. Такое состояние тела называется перегрузкой.
По второму закону Ньютона:
или в проекции на ось :
откуда
По третьему закону Ньютона:
Перегрузки испытывают космонавты при взлете и на участках торможения космического корабля, летчики при выполнении фигур высшего пилотажа, пассажиры лифта при разгоне или торможении лифта и т.д.
- Если тело движется с ускорением, направленным вертикально вниз, вес тела уменьшается.
По второму закону Ньютона:
или в проекции на ось :
откуда
По третьему закону Ньютона:
Если ускорение тела в этом случае будет равно ускорению свободного падения, вес тела равен нулю, т. е. тело будет находиться в состоянии невесомости.
е. тело будет находиться в состоянии невесомости.
Поскольку вес покоящегося тела равен силе тяжести, часто считают, что вес и сила тяжести – это одна и та же сила. Однако это неверно. Во-первых, вес и сила тяжести приложены к разным телам: сила тяжести приложена к телу, а вес – к опоре или подвесу. Во-вторых, вес и сила тяжести имеют различную физическую природу: вес, как правило, является силой упругости, а сила тяжести – это сила гравитационного взаимодействия. Наконец, как было показано выше, вес тела изменяется с изменением ускорения и может быть равен нулю, когда сила тяжести нулю не равна.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
Сила тяжести, вес тела, сила упругости.
 Примеры решения задач по физике. 7 класс
Примеры решения задач по физике. 7 классСила тяжести, вес тела, сила упругости. Примеры решения задач по физике. 7 класс
- Подробности
- Просмотров: 1434
Задачи по физике — это просто!
Вспомним
Изображение сил на чертеже:
Формула для расчета силы тяжести, действующей на тело:
Формула для расчета веса тела:
Форула для расчета силы упругости:
Здесь единица измерения массы — 1 кг,
единица измерения силы — 1 Н,
единица измерения жесткости пружины — 1 Н/м,
единица измерения величины деформации пружины (удлинения) — 1 м.
Все задачи решаем в системе СИ!
А теперь к задачам!
Элементарные задачи для 7 класса из курса школьной физики на расчет силы тяжести, веса тела и силы упругости.
Задача 1
Определить силу тяжести, действующую на тело массой 100 кг.
Задача 2
Определить вес тела массой 600 г.
Задача 3
Определить массу тела весом 120 Н.
Задача 4
На полу стоит ящик массой 1 тонна. Определить силу тяжести и силу упругости, действующие на ящик, а также вес ящика.
(Здесь N — сила реакции опоры, на которой стоит ящик, приложена к ящику, является силой упругости.
Если тело стоит неподвижно, т.е. не проваливается сквозь опору, то сила реакции опоры численно равна силе тяжести, действующей на тело.
Вес тела приложен к опоре и численно равен силе тяжести, действующей на тело.)
Задача 5
Определить вес алюминиевого бруска объемом 200 см3.
Задача 6
Определить силу упругости, возникающую при сжатии пружины на 10 см, если жесткость пружины равна 400 Н/м.
Задача 7
Определить максимальную силу упругости, возникающую при растяжении резины грузом массой 5 кг.
Задача 7
Найти удлинение пружины, возникающее под действием подвешенного к ней груза массой 200 г, если жесткость пружины равна 1000 Н/м.
(в этой задаче Х -это удлинение пружины, иначе величина деформации пружины, равна изменению длины пружины при деформации)
Зависимость веса тела от вида движения в физике
Зависимость веса тела от вида движения:
В настоящее время большинство административных и жилых зданий являются многоэтажными. Для подъема на верхние этажи и спуска вниз пользуются лифтами. Рассмотрим движение человека, поднимающегося и опускающегося в лифте.
1. Человек с массой
Иначе говоря, при движении лифта с постоянной скоростью вес тела будет таким же, каким он был, когда лифт находился в покое (рис. 2.5а).
2. Лифт двигается вниз с ускорением (рис. 2.5 б). Согласно второму закону Ньютона:
Здесь – сила реакции пола лифта, – масса тела.
По третьему закону Ньютона, вес тела . С учетом формулы (2.7) получаем
Итоговый вес тела во время движения будет:
Отсюда видно, что когда лифт двигается вниз с ускорением , вес человека уменьшается на величину . Если резко освободить трос, который держит лифт, то лифт будет двигаться вниз с ускорением , а вес человека будет:
Если резко освободить трос, который держит лифт, то лифт будет двигаться вниз с ускорением , а вес человека будет:
Состояние, при котором сила взаимодействия тела с опорой или подвесом равна нулю, называется невесомостью.
Значит, чтобы тело перешло в невесомое состояние, оно должно двигаться вниз с ускорением . Отсюда вытекает, что во время свободного падения тела находятся в невесомом состоянии. Частичное состояние невесомости наблюдается при раскачивании на качелях в момент спуска и во время прыжка. Это продолжается очень короткое время. Космонавты, проживающие в искусственных спутниках Земли и на орбитальных станциях, находятся долгое время в состоянии невесомости. В этот период нарушается система кровообращения и питания организма. Для профилактики отрицательных последствий состояния невесомости на орбитальных станциях предпринимаются специальные меры.
3. Лифт поднимается вверх с ускорением (рис. 2.5в). Воздействие, оказываемое человеком на пол (опору) лифта, равняется:
Отсюда видно, что при подъеме лифта вверх с ускорением, вес человека увеличивается на величину . Это называется дополнительная нагрузка (перегрузка).
Это называется дополнительная нагрузка (перегрузка).
Перегрузка определяется отношением веса тела при движении с ускорением к весу тела в состоянии покоя:
В этом состоянии полная нагрузка приходится на опору. Однако появляются частичные нагрузки на тело человека. Например, вес головы человека давит на шею, вес головы, шеи, плеч и рук давит на корпус и т.д., к ногам. Если ускорение лифта будет в пределе 0,3 – 1 м/с2 , то человек этого не почувствует. Но в сверхзвуковых самолетах, при взлете ракеты ускорение доходит до 100 м/с2. По рассказам летчиков и космонавтов, которые находились в этом состоянии, перегрузка прижимала их к креслам, поднять руки было очень трудно, даже открыть глаза удавалось с
трудом.
Образец решения задачи:
Лифт опускается вниз с ускорением 4,5 м/с2. Во сколько раз уменьшается вес тела, находящегося в лифте?
Дано:
Найти:
Формула:
Решение:
Ответ: 1,82 раза.
понятие, формулы для расчета, схема, коэффициент и отличие от силы тяжести
Что такое сила веса
Вес тела является силой влияния этого тела на опору в виде подвеса или иной разновидности крепления, которая препятствует падению, и возникает в области воздействия силы тяжести.
Вес тела в единицах СИ измеряется в Ньютонах (Н).
Термин «вес» обычно не применяется в законах в физике. Чаще всего используют понятия «масса» и «сила». Более содержательная величина — это сила воздействия на опору. Если ее рассчитать, то можно, к примеру, оценить абсолютную способность опоры стабилизировать положение рассматриваемого тела в определенных условиях.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
История понятия
Еще древнегреческие философы оперировали определениями тяжести и легкости тел, как неотъемлемыми их физическими свойствами.
- Согласно Платону, вес является естественной тенденцией объектов искать себе подобные.
- Аристотель понимал легкость, как свойство в восстановлении порядка ключевых компонентов, включая воду, воздух, землю и огонь.
- Это качество Архимедом определялось, как противоположное плавучести.
- Евклид впервые представил контактное определение веса. Оно заключалось в том, что данная величина является легкостью одной вещи в сравнении с другой, измеряемой балансом.
В 1901 году была проведена третья Генеральная конференция по мерам и весам. В рамках мероприятия было подчеркнуто, что понятие «вес» соответствует величине аналогичной природы, что и определение «сила». На конференции было отмечено понятие веса тела, как произведение массы тела на ускорение, вызванное гравитацией. Стандартным весом тела было принято называть произведение массы тела и стандартного ускорения, которое составляет 980,665 см/с2.
Способы измерения
Прибором, позволяющим измерить вес тела, являются пружинные весы. Если они градуированы, то с их помощью можно определить массу тела.
Принцип действия рычажных весов заключается в сравнении масс объектов, которые подвержены воздействию равного ускорения свободного падения, либо суммы ускорений в случае неинерциальных систем отсчета.
Если используют технические пружинные весы, то ускорение свободного падения, как правило, не учитывают. Это связано с минимальным влиянием этой величины на измерения, которая меньше, чем практически необходимая точность взвешивания.
Для газообразной и жидкой среды характерно действие силы Архимеда, что объясняет разницу измерений веса по сравнению с взвешиванием аналогичного тела в вакууме.
Важные формулы для расчета веса тела
В том случае, когда тело находится в состоянии покоя в условиях инерциальной системы отсчета, его вес Р будет равен силе тяжести, которая воздействует на тело, пропорционален массе m и ускорению свободного падения g в рассматриваемой точке.
Формула для расчета веса имеет вид:
P = m * g
Ускорение свободного падения является зависимой величиной. Оно определяется высотой над поверхностью Земли, а также географическими координатами точки измерения.
В результате вращения Земли в течение суток наблюдается широтное уменьшение веса. Таким образом, данная величина на экваторе будет меньше, чем на полюсах. Значение g также меняется в связи с гравитационными аномалиями. Они объясняются неодинаковым строением поверхности планеты. Если объект находится не на Земле, а близко к поверхности другой планеты, то величина ускорения свободного падения будет определяться массой и габаритами этой планеты.
Невесомость — отсутствие веса. Данное состояние возможно при удалении тела от объекта, который его притягивал, либо в том случае, когда тело пребывает в свободном падении, то есть:
g – w = 0
Тело, масса которого m, может быть подвержено воздействию других сил. Такие силы обусловлены гравитационным полем. Примерами являются сила Архимеда и сила трения.
Такие силы обусловлены гравитационным полем. Примерами являются сила Архимеда и сила трения.
Отличие силы веса тела от силы тяжести
Термины силы тяжести и веса отличаются. Оба понятия применимы для теории гравитационного поля в физике. Нередко их неверно используют в разном контексте. Это связано с тем, что в стандартном понимании такие определения, как масса в виде свойства материи и вес, воспринимаются в качестве тождественных. По этой причине важно правильно понимать тяжесть и вес тела при рассмотрении научных вопросов. Часто эти две концепции применяются, как взаимозаменяемые.
Сила, направленная на тело со стороны Земли или другого астрономического объекта, является силой тяжести:
F (тяж) = m * g
Сила воздействия тела на опору или вертикальный подвес является весом тела, которая обозначена буквой W и представляет собой векторную величину.
При этом наблюдают процесс отталкивания атомов или молекул объекта от частиц основания. В результате:
В результате:
- появляется частичная деформация опоры и объекта;
- возникают силы упругости;
- незначительно изменяется форма тела и опоры;
- возникает сила реакции опоры и сила упругости на поверхности тела.
Примеры задач для расчета веса тела
Задача № 1Требуется определить массу шара из свинца, если его вес составляет 600 Н.
Решение:
P = m * g
m = P / g
m = 600 / 10 = 60
Ответ: масса шара равна 60 килограмм.
Задача № 2Имеется футбольный мяч, который весит 400 грамм. Требуется вычислить его вес и силу тяжести, оказывающую на него воздействие.
Решение:
P = F (тяж) = m * g
P = F (тяж) = 0,4 * 10 = 4
Ответ: вес мяча и сила тяжести равны 4 Н.
Задача № 3Необходимо определить вес воды, объем которой составляет 3 кубических дециметра.
Решение:
P = m * g
m = p * V
m = 1000 * 0. 003 = 3
003 = 3
Р = 3 * 9.8 = 29.4
Ответ: вес воды равен 29,4 Н.
Задача № 4К потолку подвешена люстра. Она действует на подвес с силой 49 Н. Требуется определить массу люстры.
Решение:
P = m * g
m = P / g
m = 49 / 9.8 = 5
Ответ: масса люстры составляет 5 килограмм.
Вес на других планетах
Вес тела зависит от гравитационного ускорения. Притяжение на других планетах определяется их массой и удалением поверхности от центра тяжести. Сравнить гравитационные ускорения можно с помощью таблицы:
Универсальное уравнение для оценки идеальной массы тела и массы тела при любом ИМТ
Am J Clin Nutr. 2016 May; 103 (5): 1197–1203.
Кортни М. Петерсон
2 Лаборатория физиологии скелетных мышц Джона С. Макилхенни и
Диана М. Томас
4 Центр количественных исследований ожирения, Государственный университет Монклера, Монклер, Нью-Джерси;
Джордж Л.
 Блэкберн
Блэкберн5 Центр изучения медицины питания, Медицинский центр Бет Исраэль Дьяконис, Бостон, Массачусетс; и
6 Отдел питания Гарвардской медицинской школы, Бостон, Массачусетс
Стивен Б. Хеймсфилд
3 Лаборатория метаболизма и состава тела, Центр биомедицинских исследований Пеннингтона, Система государственного университета Луизианы, Батон-Руж, Луизиана;
2 Лаборатория физиологии скелетных мышц Джона С. Макилхенни и
3 Лаборатория метаболизма и состава тела, Центр биомедицинских исследований Пеннингтона, Университет штата Луизиана, Батон-Руж, Луизиана;
4 Центр количественных исследований ожирения, Государственный университет Монклера, Монклер, Нью-Джерси;
5 Центр изучения медицины питания, Медицинский центр диаконис Бет Исраэль, Бостон, Массачусетс; и
6 Отдел питания Гарвардской медицинской школы, Бостон, Массачусетс и Центр трансляционных наук.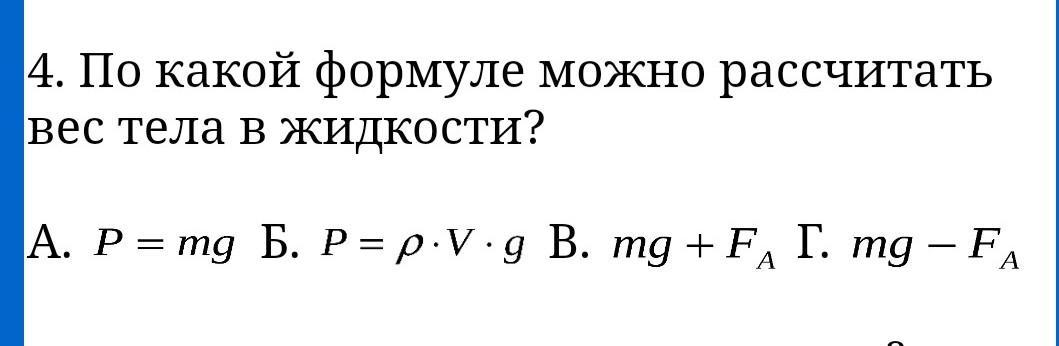
Поступила 7 августа 2015 г .; Принято 25 февраля 2016 г.
Авторские права © Американское общество питания, 2016 г.См. Статью на странице 1193.
На эту статью цитировали другие статьи в PMC.Abstract
Предпосылки: Уравнения идеальной массы тела (IBW) и диапазоны индекса массы тела (BMI) использовались для определения диапазонов здорового или нормального веса, хотя эти два разных подхода расходятся друг с другом. В частности, прошлые уравнения IBW несовместимы со значениями ИМТ, и, в отличие от ИМТ, в уравнениях не учитывается наличие диапазона идеальной или целевой массы тела.
Цель: Впервые, насколько нам известно, мы объединили концепции линейного уравнения IBW и определения целевого веса тела с точки зрения ИМТ.
Дизайн: С использованием расчетов и приближений мы получили простое в использовании линейное уравнение, которое врачи могут использовать для расчета как IBW, так и массы тела при любом целевом значении BMI.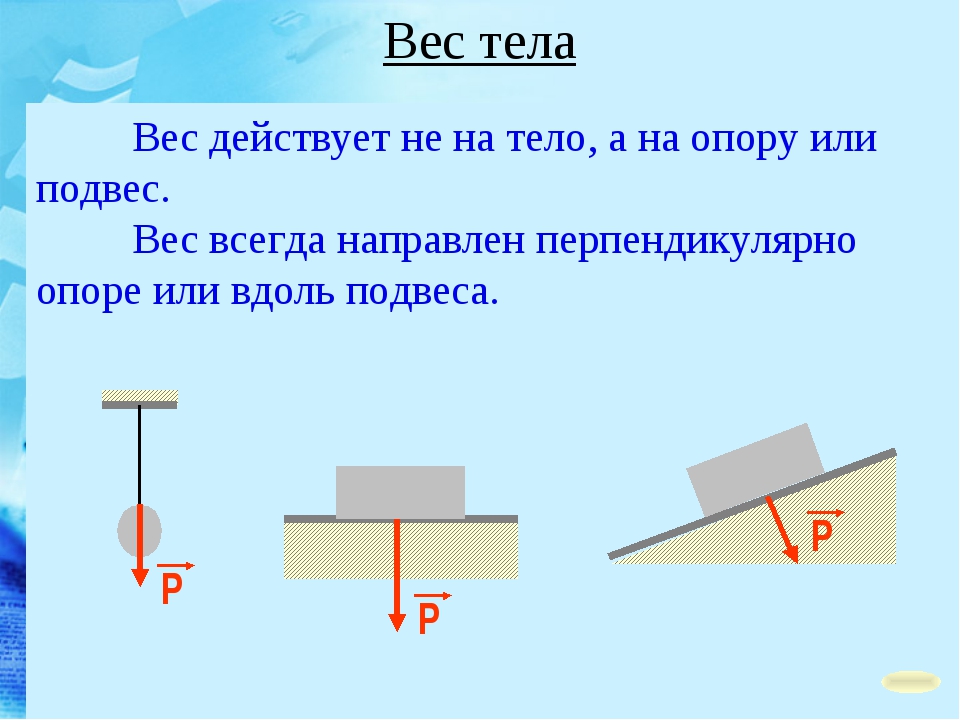 Мы измерили эмпирическую точность уравнения с использованием данных NHANES и провели сравнительный анализ с предыдущими уравнениями IBW.
Мы измерили эмпирическую точность уравнения с использованием данных NHANES и провели сравнительный анализ с предыдущими уравнениями IBW.
Результаты: Наше линейное уравнение позволило нам рассчитать массу тела для любого ИМТ и роста со средней эмпирической точностью 0,5–0,7% на основе данных NHANES. Более того, мы показали, что наше уравнение веса тела напрямую согласуется со значениями ИМТ как для мужчин, так и для женщин, что позволяет избежать проблем с переоценкой и недооценкой на верхнем и нижнем концах спектра роста, которые преследовали предыдущие уравнения IBW.
Выводы: Наше линейное уравнение увеличивает сложность уравнений IBW, заменяя их одним универсальным уравнением, которое рассчитывает как IBW, так и массу тела при любом целевом ИМТ и росте.Таким образом, наше уравнение совместимо с ИМТ и может применяться с использованием математических вычислений или калькулятора без необходимости в приложении, что делает его полезным инструментом как для практикующих врачей, так и для широкой публики.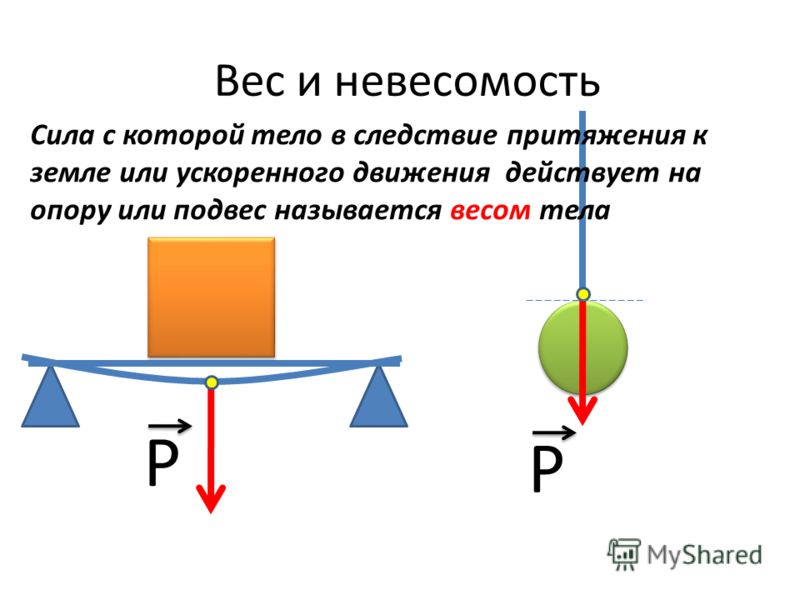
Ключевые слова: ИМТ, идеальная масса тела, ожирение, избыточный вес, упрощенные уравнения
См. Соответствующую редакционную статью на странице 1193.
ВВЕДЕНИЕ
Как точно определить желаемый или целевой вес тела для оценки питания и здоровья был важным вызов уже более века (1, 2).Многие из первых попыток были основаны на актуарных данных и определяли идеальный или желаемый вес тела с использованием таблиц роста и веса. Поскольку эти таблицы громоздки в использовании, уравнения идеальной массы тела (IBW) для прогнозирования веса как линейной функции от роста были разработаны, начиная с конца 1800-х годов (2). Позже популярность уравнений IBW возросла после того, как Хамви (3) и Девайн (4) опубликовали свои основополагающие уравнения (4). Десять лет спустя, мотивированные приложениями к дозированию лекарств, Robinson et al.(5) и Miller et al. (6) сформулировали уравнения IBW на основе таблиц роста и веса Metropolitan Life Insurance Company 1959 и 1983 годов соответственно. Совсем недавно Хаммонд (7) создал метрическую версию уравнения Хамви. Хотя уравнения IBW не так популярны, как когда-то, они все еще используются клиницистами для расчета дозировки лекарств, оценки статуса избыточного и недостаточного веса, а также для расчета потребления питательных веществ (2).
Совсем недавно Хаммонд (7) создал метрическую версию уравнения Хамви. Хотя уравнения IBW не так популярны, как когда-то, они все еще используются клиницистами для расчета дозировки лекарств, оценки статуса избыточного и недостаточного веса, а также для расчета потребления питательных веществ (2).
Преимущество уравнений IBW заключается в том, что они предсказывают вес (переменная: Wt) как линейная функция от высоты (переменная: Ht) как
, где a — наклон, а b — точка пересечения.Часто термин «рост» выражается как разница от эталонного значения, такого как рост в дюймах, превышающий 5 футов. Например, уравнения Хамви (3) для конкретных полов, разработанные для системы США, оценивают IBW для для мужчин —
, а для женщин —
, тогда как уравнения Девайна (4) для конкретных полов, которые были разработаны для метрической системы, оценивают IBW для мужчин как
, а для женщин как
, где Ht выражается в дюймах, а Ht составляет ≥60 дюймов. Простая линейная структура этих уравнений позволяет легко вычислить их с помощью мысленной математики или калькулятора.
Простая линейная структура этих уравнений позволяет легко вычислить их с помощью мысленной математики или калькулятора.
Однако, несмотря на преимущество простоты, подход IBW имеет 3 важных ограничения. Во-первых, хотя IBW или желаемый вес изначально определялся как вес, связанный с наибольшей ожидаемой продолжительностью жизни на каждом росте, не существует единого идеального веса, универсально применимого ко всем сопутствующим заболеваниям и причинам, связанным со смертностью, и не существует единого идеального веса, который можно было бы использовать. применимо ко всем демографическим факторам, включая возраст и этническую принадлежность (8). Во-вторых, уравнения IBW предсказывают единственную целевую массу тела, тогда как большинство клиницистов предпочитают диапазон целевых масс тела, а эмпирические данные подтверждают это.В-третьих, Shah et al. (2) проанализировали уравнения IBW и показали, что они несовместимы с BMI и, вместо этого, что уравнения IBW занижали массу тела при меньшем росте и завышали массу тела при более высоком росте (2).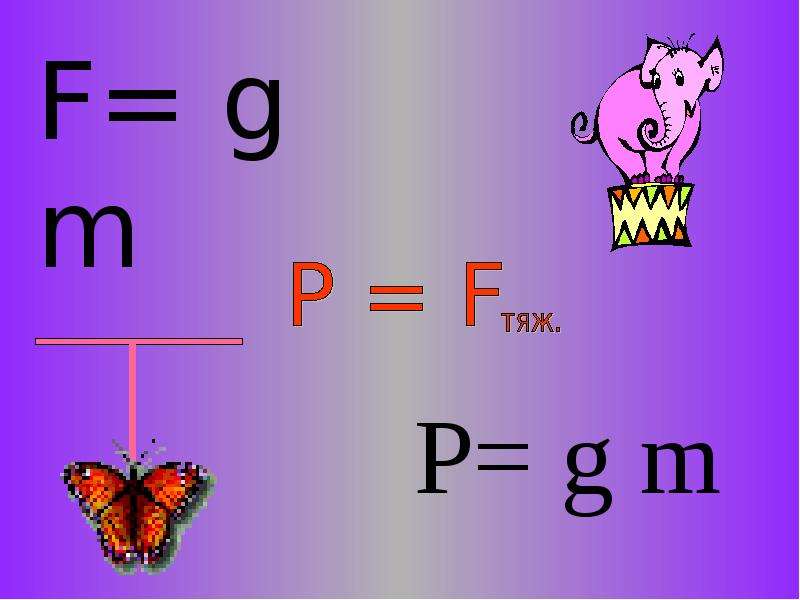 По этим причинам уравнения IBW в значительной степени были заменены диапазонами BMI.
По этим причинам уравнения IBW в значительной степени были заменены диапазонами BMI.
Напротив, ИМТ, который определяется как масса тела, разделенная на квадрат роста (кг / м 2 ), в настоящее время более широко используется в клинических условиях для диагностики избыточного ожирения и недостаточного веса (9–11).ИМТ имеет два важных преимущества: он позволяет количественно оценить ожирение независимо от роста, и врачи могут использовать ИМТ для определения целевого диапазона веса. Диапазон ИМТ 18,5–24,9 часто рассматривается как диапазон идеального или здорового веса тела [хотя более свежие данные, например, предоставленные Flegal et al. (12) предположили, что несколько более высокие ИМТ связаны с более низкой смертностью], тогда как ИМТ варьируется для статуса избыточного веса (25,0–29,9), ожирения 1 класса (30–34,9; низкий риск), ожирения 2 класса (35.0–39,9; умеренный риск) и ожирение 3 класса (≥40,0; высокий риск) используются для определения риска сопутствующих заболеваний, связанных с ожирением. Таким образом, хотя ИМТ сложнее рассчитать, и врачи часто используют приложения для его расчета, этот недостаток обычно перевешивается тем фактом, что можно назначить диапазон целевых весов и что диапазоны более точно связаны с результатами для здоровья.
Таким образом, хотя ИМТ сложнее рассчитать, и врачи часто используют приложения для его расчета, этот недостаток обычно перевешивается тем фактом, что можно назначить диапазон целевых весов и что диапазоны более точно связаны с результатами для здоровья.
Эти проблемы приводят к важному вопросу о том, действительно ли уравнения IBW и ИМТ несовместимы или есть способ объединить 2 разных подхода к определению целевого веса тела.Насколько нам известно, впервые мы объединяем концепции уравнения IBW и ИМТ для определения целевого веса тела. Мы показываем, что одно линейное уравнение может оценить как IBW, так и целевую массу тела для любого BMI и роста. В процессе мы показываем, что преимущества уравнений IBW и BMI могут быть объединены в одно простое в использовании уравнение.
МЕТОДЫ
Математический вывод
Хотя концепция ИМТ предсказывает, что вес тела взрослого человека изменяется как криволинейная функция роста (т.е., Wt ∝ Ht 2 ), это соотношение можно оценить с помощью линейного уравнения в пределах 95% диапазона роста населения США (∼60–75 дюймов или ∼1,5–1,9 м) (13). Однако, в отличие от предыдущих подходов к разработке уравнений IBW, мы строго доказали, что линейная функция верна с использованием исчисления. В процессе мы использовали ключевые этапы вывода, чтобы создать новое уравнение веса тела, которое является более точным, чем предыдущие уравнения IBW, и может быть обобщено на любой ИМТ и рост.
Однако, в отличие от предыдущих подходов к разработке уравнений IBW, мы строго доказали, что линейная функция верна с использованием исчисления. В процессе мы использовали ключевые этапы вывода, чтобы создать новое уравнение веса тела, которое является более точным, чем предыдущие уравнения IBW, и может быть обобщено на любой ИМТ и рост.
Сначала мы преобразовали уравнение для веса тела как функции роста в форму
Затем мы преобразовали уравнение 6 и расширили его до контрольной высоты Ht 0 следующим образом:
, где
и Ht — это рост человека ().Используя вычислительную технику разложения Тейлора и сохраняя только члены, линейные по ΔHt, мы получили линейное приближение
Это приближение оправдано, только если процентная погрешность мала. Поскольку кривая почти линейна в диапазоне высот 95%, процентная погрешность действительно мала (). Здесь процентная погрешность определялась пренебрегаемым членом в разложении в ряд Тейлора
Эту погрешность можно вычислить напрямую. Например, если эталонная высота находится в середине диапазона высот 95%, максимальная процентная ошибка равна 1.0%.
Например, если эталонная высота находится в середине диапазона высот 95%, максимальная процентная ошибка равна 1.0%.
Wt почти линейно зависит от Ht. Хотя Wt масштабируется как Ht 2 , Wt является почти линейной функцией Ht в диапазоне 95% Ht (∼1,5–1,9 м). Пример для ИМТ 27 кг / м 2 и показывает эталонный Ht ( Ht 0 ) 1,5 м и Δ Ht , который представляет собой разницу между Ht человека и эталонным Ht 0 . Ht, высота; Вес, вес.
Для согласования с предыдущими уравнениями IBW мы выбрали базовую высоту Ht 0 равной 5 футам (60.0 дюймов или 1,52 м) в системе США и 1,5 м (59,1 дюйма) в метрической системе. Однако этот выбор Ht 0 на нижнем конце 95% диапазона высоты вызывал ошибку. Поэтому мы аппроксимировали квадратичный член, показанный в уравнении 10 , компенсирующим линейным членом, который соответствовал весу тела на верхнем конце 95% диапазона роста (75 дюймов или 1,9 м). После стратегического округления наше окончательное уравнение было близко к точным касательным и секущим линиям, но дает более точную оценку веса тела, чем любая из этих линий.
После стратегического округления наше окончательное уравнение было близко к точным касательным и секущим линиям, но дает более точную оценку веса тела, чем любая из этих линий.
В нашем выводе было два ключевых шага, которые сделали наш подход превосходящим предыдущие уравнения IBW. Во-первых, найдя выражение для переменной наклона a в уравнении 1 в терминах ИМТ, наше уравнение напрямую согласуется со значениями ИМТ. Такое согласование дает то преимущество, что наше уравнение можно использовать для расчета массы тела при любом целевом значении ИМТ, что, насколько нам известно, никогда раньше не делалось для уравнения IBW. Во-вторых, если выбрать подходящий компенсирующий линейный член (как описано ранее), наше уравнение IBW станет более точным и легко запоминающимся.
Сравнительный анализ
Мы рассчитали точность выведенного нами уравнения IBW как теоретическими, так и эмпирическими методами. Теоретическая точность рассчитывалась как абсолютная ошибка и процентная погрешность между точным и прогнозируемым весом тела в 95% -ном диапазоне роста (60–75 дюймов или 1,5–1,9 м) при значениях ИМТ 20 и 35. Эмпирическая точность (оба значения: абсолютная ошибка и ошибка в процентах) была рассчитана путем применения нашего уравнения к антропометрическим данным, собранным у взрослых в рамках NHANES 1999–2006 гг.Мы также сравнили, насколько хорошо наше уравнение веса тела и другие уравнения IBW соответствуют значениям ИМТ. Согласование со значениями ИМТ — это один из методов оценки степени соответствия уравнений IBW. Чтобы определить выравнивание, мы использовали программу Mathematica (версия 10.0; Wolfram Research) для вычисления конечного интеграла процентной ошибки каждого уравнения IBW с использованием веса тела, предсказанного ИМТ, в качестве истинного веса. Конечные интегралы были оценены в диапазоне высоты 95% и разделены на разницу между верхней и нижней границами диапазона высоты 95%, чтобы получить среднюю точность.Этот процесс повторяли для каждого значения ИМТ от 17,0 до 27,0 с шагом 0,1, и наименьшее значение средней процентной ошибки в этом диапазоне ИМТ принималось за истинную процентную ошибку для каждого уравнения IBW.
Эмпирическая точность (оба значения: абсолютная ошибка и ошибка в процентах) была рассчитана путем применения нашего уравнения к антропометрическим данным, собранным у взрослых в рамках NHANES 1999–2006 гг.Мы также сравнили, насколько хорошо наше уравнение веса тела и другие уравнения IBW соответствуют значениям ИМТ. Согласование со значениями ИМТ — это один из методов оценки степени соответствия уравнений IBW. Чтобы определить выравнивание, мы использовали программу Mathematica (версия 10.0; Wolfram Research) для вычисления конечного интеграла процентной ошибки каждого уравнения IBW с использованием веса тела, предсказанного ИМТ, в качестве истинного веса. Конечные интегралы были оценены в диапазоне высоты 95% и разделены на разницу между верхней и нижней границами диапазона высоты 95%, чтобы получить среднюю точность.Этот процесс повторяли для каждого значения ИМТ от 17,0 до 27,0 с шагом 0,1, и наименьшее значение средней процентной ошибки в этом диапазоне ИМТ принималось за истинную процентную ошибку для каждого уравнения IBW. Этот метод нахождения наименьшей процентной ошибки правильно учитывает тот факт, что некоторые уравнения IBW согласуются с более высокими ИМТ, тогда как другие уравнения лучше согласуются с более низкими ИМТ и, таким образом, позволяют избежать несправедливого наказания определенных уравнений на этом основании.
Этот метод нахождения наименьшей процентной ошибки правильно учитывает тот факт, что некоторые уравнения IBW согласуются с более высокими ИМТ, тогда как другие уравнения лучше согласуются с более низкими ИМТ и, таким образом, позволяют избежать несправедливого наказания определенных уравнений на этом основании.
РЕЗУЛЬТАТЫ
Уравнение в системе США
Мы начали с вывода уравнения для системы США.Выведя уравнение, как описано в разделе «Методы», мы преобразовали вес в фунты, а рост в дюймы и расширили его вокруг эталонной высоты 5 футов (60 дюймов), чтобы получить
. Затем мы округлили 5,121 до 5 и пренебрегли показанным членом второго порядка. в уравнении 10 . Поскольку пренебрегая этим термином, мы немного занизили вес тела на верхнем конце 95% диапазона роста (ошибка 2,4%), мы нашли линейное приближение для замены члена второго порядка. После выполнения процедуры, изложенной в разделе «Методы», мы обнаружили, что поправочный член для уравнения 10 , необходимый для получения правильного веса на верхнем конце 95% диапазона роста, равен
.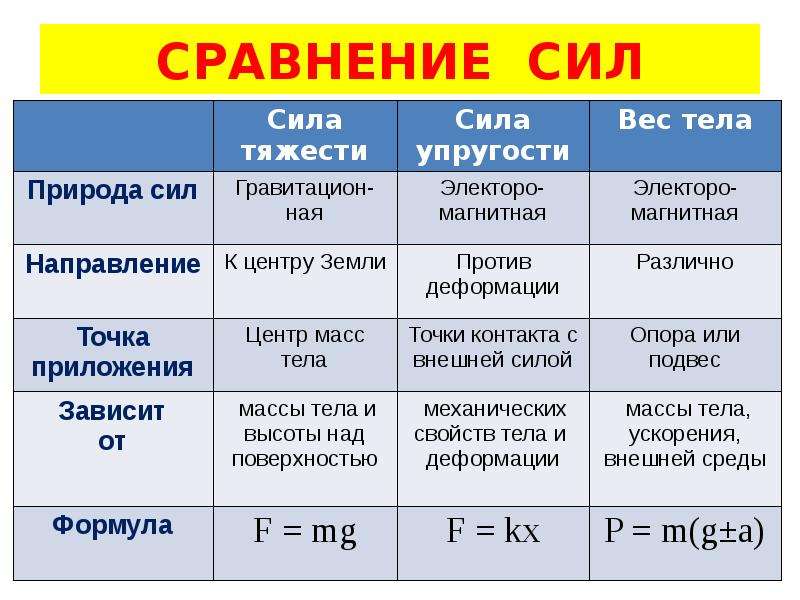 После того, как этот результат был подставлен обратно в уравнение, мы получили
После того, как этот результат был подставлен обратно в уравнение, мы получили
Клинические применения
Эта легко запоминающаяся формула обеспечивает высокоточный прогноз веса тела при любом целевом ИМТ и росте.Чтобы определить массу тела в фунтах, желаемый ИМТ умножается на 5, а затем прибавляется ИМТ / 5 фунтов на каждый дюйм роста> 5 футов. Например, для ИМТ 20 начните со 100 фунтов на рост 5 футов и добавьте 4 фунта на каждый дополнительный дюйм роста. Для ИМТ 25 начните со 125 фунтов и добавьте 5 фунтов на каждый дюйм роста. Таким образом, выразив наклон через ИМТ, мы разработали уравнение, которое действительно для прогнозирования массы тела при любом заданном ИМТ, что делает его единым универсальным уравнением.
В конкретном случае оценки IBW выбирается идеальный BMI для использования в уравнении; этот выбор объединяет концепции уравнений BMI и IBW.Например, если предположить, что ИМТ, равный 20, соответствует ИМТ, наше уравнение предсказывает, что ИМТ будет
. В качестве альтернативы, значения ИМТ в диапазоне от 18,5 до 25,0 могут быть взяты для представления диапазона ИМТ. В этом случае наше уравнение даст нижнюю границу (18,5) для IBW как
В качестве альтернативы, значения ИМТ в диапазоне от 18,5 до 25,0 могут быть взяты для представления диапазона ИМТ. В этом случае наше уравнение даст нижнюю границу (18,5) для IBW как
и верхнюю границу (25) как
. Аналогичным образом, другие диапазоны BMI также могут быть определены с помощью нашего уравнения. показаны расчеты с использованием нашего уравнения при ключевых значениях ИМТ 20, 25, 30, 35, 40, 45 и 50.Каждое увеличение ИМТ на 5 добавляет 25 фунтов к массе тела при росте 5 футов и дополнительно на 1 фунт за каждое увеличение роста на 1 дюйм; этот расчет обеспечивает удобный способ запомнить уравнение, поскольку большинство ключевых значений ИМТ кратны 5.
ТАБЛИЦА 1
Уравнение массы тела при ключевых значениях ИМТ
| ИМТ, кг / м 2 | Версия для США | Метрическая версия |
| Вес (фунт) = 5 × ИМТ + (ИМТ ÷ 5) × (Высота — 60 дюймов) | Вес (кг) = 2. 2 × ИМТ + 3,5 × ИМТ × (Ht — 1,5 м) 2 × ИМТ + 3,5 × ИМТ × (Ht — 1,5 м) | |
| 20 | Wt (фунт) = 100 + 4 × (Ht — 60 дюймов) | Wt (кг) = 44 + 70 × (Ht — 1,5 м) |
| 25 | Wt (фунт) = 125 + 5 × (Ht — 60 дюймов) | Wt (кг) = 55 + 88 × (Ht — 1,5 м) |
| 30 | Wt (фунты) = 150 + 6 × (Ht — 60 дюймов) | Wt (кг) = 66 + 105 × (Ht — 1,5 м) |
| 35 | Wt (фунты) = 175 + 7 × (Ht — 60 дюймов) | Wt (кг) = 77 + 123 × (Ht — 1.5 м) |
| 40 | Wt (фунт) = 200 + 8 × (Ht — 60 дюймов) | Wt (кг) = 88 + 140 × (Ht — 1,5 м) |
| 45 | Wt (фунты) = 225 + 9 × (Ht — 60 дюймов) | Wt (кг) = 99 + 158 × (Ht — 1,5 м) |
| 50 | Wt (фунты) = 250 + 10 × (Ht — 60 дюймов) | Wt (кг) = 110 + 175 × (Ht — 1,5 м) |
Еще одна полезная особенность уравнения состоит в том, что каждое увеличение ИМТ человека на 1 пункт добавляет
массы тела. Например, каждое увеличение ИМТ на 1 пункт добавляет 6 фунтов массы тела человеку с ростом 5 футов 5 дюймов, 7 фунтов тому, чей рост составляет 5 футов 10 дюймов, и 8 фунтов тому, чей рост составляет 6 футов 3 дюйма. in. Знание о том, что потеря того же постоянного количества фунтов приблизительно снижает ИМТ человека на 1 пункт, может быть полезной и мотивирующей целью для людей, которые пытаются похудеть. И наоборот, при инверсии этого отношения ИМТ человека можно оценить, разделив массу его тела (в фунтах) на 6 фунтов, если рост человека составляет 5 футов 5 дюймов, на 7 фунтов, если рост человека составляет 5 футов 10 дюймов, и на 8 фунтов, если рост человека 6 футов 3 дюйма.Этот метод позволяет человеку быстро оценить ИМТ.
Например, каждое увеличение ИМТ на 1 пункт добавляет 6 фунтов массы тела человеку с ростом 5 футов 5 дюймов, 7 фунтов тому, чей рост составляет 5 футов 10 дюймов, и 8 фунтов тому, чей рост составляет 6 футов 3 дюйма. in. Знание о том, что потеря того же постоянного количества фунтов приблизительно снижает ИМТ человека на 1 пункт, может быть полезной и мотивирующей целью для людей, которые пытаются похудеть. И наоборот, при инверсии этого отношения ИМТ человека можно оценить, разделив массу его тела (в фунтах) на 6 фунтов, если рост человека составляет 5 футов 5 дюймов, на 7 фунтов, если рост человека составляет 5 футов 10 дюймов, и на 8 фунтов, если рост человека 6 футов 3 дюйма.Этот метод позволяет человеку быстро оценить ИМТ.
Практический пример, показывающий, как можно использовать это уравнение, можно увидеть в его применении к пациенту с массой тела 225 фунтов и ростом 5 футов 10 дюймов (или 70 дюймов). Если клиницист хочет знать, страдает ли пациент ожирением и какой вес ему необходимо сбросить, чтобы достичь верхнего предела диапазона IBW, быстрый расчет показывает, что вес пациента при ИМТ ожирения 30 составляет
, тогда как при верхний предел диапазона здорового ИМТ (<25), пациент будет иметь вес
Таким образом, мы классифицируем пациента как страдающего ожирением, и ему или ему нужно будет сбросить 50 фунтов, чтобы считаться нормальным или здоровым диапазон веса. Конечно, для многих пациентов цель по снижению веса на 5–10% может быть более реалистичной, и наше уравнение может учитывать такие персонализированные цели, поскольку оно позволяет оценить массу тела для любого желаемого целевого ИМТ. Например, если ИМТ 28,0 является желаемой целью пациента, целевой вес пациента будет
Конечно, для многих пациентов цель по снижению веса на 5–10% может быть более реалистичной, и наше уравнение может учитывать такие персонализированные цели, поскольку оно позволяет оценить массу тела для любого желаемого целевого ИМТ. Например, если ИМТ 28,0 является желаемой целью пациента, целевой вес пациента будет
Уравнение в метрической системе
Для метрической системы мы использовали ту же математическую процедуру, что и для системы США. Уравнение:
, где мы округлили все члены до одного десятичного знака.Для справки: если мы возьмем версию уравнения для США и напрямую переведем ее в метрические единицы, то получим 3,6 вместо 3,5. Однако значение 3,5 дает более низкую совокупную процентную ошибку в диапазоне 95% высоты и, таким образом, является предпочтительным.
Точность
Наше уравнение очень точное. В, мы проиллюстрировали теоретическую точность нашего уравнения для ИМТ 20 и 35. За исключением высоты ≤61 дюйм (≤1,53 м), уравнение предсказывает правильный вес с точностью до 1 фунта (0. 5 кг) для ИМТ 20 и с точностью до 2 фунтов (1 кг) для ИМТ 35. Точность нашего уравнения, измеренная с помощью процентной ошибки, не зависит от ИМТ; таким образом, более высокие ИМТ не приводят к большему проценту ошибок. Максимальная процентная погрешность в 95% диапазоне высоты составляет 2,4% для обеих версий уравнения, а уравнение наиболее точное в середине диапазона высот, что является следствием того факта, что оно было разработано таким образом, чтобы минимизировать процентную ошибку. . Наконец, применительно к данным NHANES, наше уравнение дало среднюю эмпирическую точность 0.7% (95% ДИ: 0%, 3,2%) и 0,5% (95% ДИ: 0,3%, 2,4%) для версии США и метрической системы соответственно; это соответствовало средней абсолютной погрешности 1,1 фунта и 0,4 кг соответственно. Ошибка была вызвана в основном людьми с коротким и высоким концом диапазона роста, а влияние ковариат, таких как возраст, было опосредовано лишь косвенно, через их влияние на рост.
5 кг) для ИМТ 20 и с точностью до 2 фунтов (1 кг) для ИМТ 35. Точность нашего уравнения, измеренная с помощью процентной ошибки, не зависит от ИМТ; таким образом, более высокие ИМТ не приводят к большему проценту ошибок. Максимальная процентная погрешность в 95% диапазоне высоты составляет 2,4% для обеих версий уравнения, а уравнение наиболее точное в середине диапазона высот, что является следствием того факта, что оно было разработано таким образом, чтобы минимизировать процентную ошибку. . Наконец, применительно к данным NHANES, наше уравнение дало среднюю эмпирическую точность 0.7% (95% ДИ: 0%, 3,2%) и 0,5% (95% ДИ: 0,3%, 2,4%) для версии США и метрической системы соответственно; это соответствовало средней абсолютной погрешности 1,1 фунта и 0,4 кг соответственно. Ошибка была вызвана в основном людьми с коротким и высоким концом диапазона роста, а влияние ковариат, таких как возраст, было опосредовано лишь косвенно, через их влияние на рост.
ТАБЛИЦА 2
Точность уравнения массы тела 1
| Система США | Метрическая система | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| BMI | Высота, дюймы | фунтов | Вес, фунт | Расчетный | Абсолютная погрешность, фунт | Высота, м | Вес, кг | Прогнозируемая масса, кг | Абсолютная погрешность, кг | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20 кг / м 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 60 | 102 | 100 | −2 | 1. 50 50 | 45,0 | 44,0 | -1,0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 61 | 106 | 104 | -2 | 1,53 | 46,8 | 46,1 | 46,1 | 109 | 108 | −1 | 1,56 | 48,7 | 48,2 | −0,5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 63 | 113 | 112 | −1 | 112 | −1 | 6 | 50,3 | −0,3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 64 | 117 | 116 | −1 | 1,62 | 52,5 | 52,4 | −0,1 |
Сравнение с другими уравнениями IBW Наконец, мы сравнили наше уравнение веса тела с другими уравнениями IBW () на предмет их согласованности. ТАБЛИЦА 3
ТАБЛИЦА 4Согласование уравнений IBW с BMI 1
ОБСУЖДЕНИЕ В этой статье мы улучшили концепцию уравнения IBW, повысив его строгость и расширив область действия. С помощью простых расчетов и приближений мы объединили концепции 1 ) уравнений IBW и 2 ) использования ИМТ для определения диапазонов идеальной и целевой массы тела. До нашей работы предполагалось, что концепции уравнений IBW и BMI несовместимы. Уравнения IBW предсказывают одиночный IBW как линейную функцию от высоты. Напротив, ИМТ используются для определения диапазона целевого веса тела как квадратичной функции от роста. Мы согласовали 2 противоположных подхода с использованием исчисления для линеаризации уравнения, определяющего ИМТ.Поскольку мы сохранили наклон на линеаризованного уравнения в терминах ИМТ (т. Е. Оставив наклон как переменную, а не как постоянное число), мы смогли разработать уравнение, которое предсказывает массу тела при любом ИМТ, а не при единственном ИМТ. Хотя за последние несколько десятилетий было разработано несколько уравнений IBW, наше уравнение веса тела имеет важные преимущества. Во-вторых, наше уравнение является очень точным и позволяет избежать проблемы несоответствия со значениями ИМТ, которая является проблемой, которая мешает другим уравнениям IBW.Shah et al. (2) провели сравнительный анализ уравнений IBW и пришли к выводу, что ни одно из уравнений IBW не было согласовано с одним ИМТ, а скорее находилось в диапазоне от ~ 18,5 до ≥25,0. Поскольку наше уравнение массы тела объединяет концепции уравнений IBW и ИМТ, оно имеет те же ограничения, что и ИМТ.ИМТ ошибочно классифицирует значительную часть населения на основании ожирения, включая людей с саркопеническим ожирением и людей с очень высокой мускулатурой. Действительно, ИМТ лучше всего рассматривать как антропометрический индикатор первого уровня для выявления ожирения. Поскольку наше уравнение так близко соответствует значениям ИМТ в диапазоне роста 95% (ошибка 0,5%), оно страдает теми же ограничениями при прогнозировании состава тела. Во-вторых, оптимальный диапазон ИМТ может варьироваться в зависимости от пола, возраста, этнической или расовой принадлежности, сопутствующей патологии или смертности, связанных с конкретной причиной, или других факторов. Несмотря на эти недостатки, масса тела и ИМТ остаются двумя наиболее часто сообщаемыми переменными оценки питания (16). Точно так же уравнения IBW все еще используются, хотя и в меньшей степени, для диагностики статуса недостаточного и избыточного веса, для расчета потребления питательных веществ и для дозирования лекарств. В частности, для дозирования лекарств IBW используется как суррогат безжировой массы тела (5). Распространенным альтернативным подходом к дозированию является использование IBW плюс множитель разницы между общим весом и IBW для получения эффективной массы тела, которая является промежуточной между IBW и фактической массой тела (17).Наше уравнение может заменить этот подход к дозированию лекарств, потому что наше уравнение можно использовать с ИМТ, выбранным как промежуточное значение между идеальным и фактическим ИМТ человека, и выбранное значение может быть адаптировано к липофобным свойствам каждого лекарства. Следовательно, в дополнение к предоставлению быстрой оценки веса тела для оценки питания и состава тела, наше уравнение может быть использовано в будущем для упрощения расчетов дозировки лекарств. В заключение, наше универсальное уравнение веса тела превосходит предыдущие уравнения IBW, поскольку оно предсказывает как IBW, так и массу тела для любого ИМТ и роста с высокой степенью точности.Наше уравнение можно настроить так, чтобы оно соответствовало любому значению ИМТ, что делает уравнение универсальным и актуальным для ряда сценариев. Более того, наше уравнение не зависит от пола, а коэффициенты в системе США являются кратными или делителями 5, что упрощает запоминание и упрощает вычисление с использованием мысленной математики или калькулятора и без использования приложения. Следовательно, наше уравнение должно быть привлекательным для практикующих врачей и широкой публики. Благодарности Обязанности авторов заключались в следующем: CMP: написал рукопись и взял на себя основную ответственность за окончательное содержание рукописи; CMP, DMT и SBH: участвовали в математических расчетах; CMP, GLB и SBH: разработали исследование; и все авторы: прочитали и одобрили рукопись. ССЫЛКИ1. Пай М.П., Палоучек Ф.П. Происхождение «идеальных» уравнений веса тела. Энн Фармакотер 2000; 34: 1066–9. [PubMed] [Google Scholar] 2. Шах Б., Сучер К., Холленбек CB. Сравнение уравнений идеальной массы тела и опубликованных таблиц роста и веса с таблицами индекса массы тела для здоровых взрослых в США. Нутр Клин Практ 2006; 21: 312–9. [PubMed] [Google Scholar] 3. Hamwi GJ. Терапия: изменение диетических представлений.Нью-Йорк: Американская диабетическая ассоциация; 1964. [Google Scholar] 4. Дивайн Б.Дж. Гентамициновая терапия. Препарат Интелл Клин Фарм 1974. 8: 650–5. [Google Scholar] 5. Робинсон Дж. Д., Лупкевич С. М., Паленик Л., Лопес Л. М., Ариет М. Определение идеальной массы тела для расчета дозировки лекарств. Am J Hosp Pharm 1983; 40: 1016–9. [PubMed] [Google Scholar] 6. Миллер Д.Р., Карлсон Д.Д., Ллойд Б.Дж., Дэй Б.Дж. Определение идеальной массы тела (и массы). Am J Hosp Pharm 1983; 40: 1622–5. [Google Scholar] 7. Хаммонд К.А.
Диетическая и клиническая оценка.В: Махан Л.К., Пень С.Е., редакторы. Еда, питание и диетотерапия Краузе. 11-е изд.
Филадельфия: Сондерс; 2000. с. 353–79. [Google Scholar] 10. Джин Дж.
Страница пациента JAMA. Лекарства для похудания: показания и применение. JAMA
2015; 313: 2196. [PubMed] [Google Scholar] 11. Икрамуддин С., Блэкстоун Р.П., Бранкатисано А., Тули Дж., Шах С.Н., Вулф Б.М., Фуджиока К., Махер Дж. У., Суэйн Дж., Ку Ф. Г. и др. .
Влияние обратимой прерывистой интраабдоминальной блокады блуждающего нерва на патологическое ожирение: рандомизированное клиническое исследование ReCharge.JAMA
2014; 312: 915–22. [PubMed] [Google Scholar] 12. Flegal KM, Kit BK, Orpana H, Graubard BI.
Связь общей смертности с избыточной массой тела и ожирением с использованием стандартных категорий индекса массы тела: систематический обзор и метаанализ. JAMA
2013; 309: 71–82. [Бесплатная статья PMC] [PubMed] [Google Scholar] 13. Макдауэлл MA, Fryar CD, Ogden CL, Flegal KM. [Google Scholar] 7. Хаммонд К.А.
Диетическая и клиническая оценка.В: Махан Л.К., Пень С.Е., редакторы. Еда, питание и диетотерапия Краузе. 11-е изд.
Филадельфия: Сондерс; 2000. с. 353–79. [Google Scholar] 10. Джин Дж.
Страница пациента JAMA. Лекарства для похудания: показания и применение. JAMA
2015; 313: 2196. [PubMed] [Google Scholar] 11. Икрамуддин С., Блэкстоун Р.П., Бранкатисано А., Тули Дж., Шах С.Н., Вулф Б.М., Фуджиока К., Махер Дж. У., Суэйн Дж., Ку Ф. Г. и др. .
Влияние обратимой прерывистой интраабдоминальной блокады блуждающего нерва на патологическое ожирение: рандомизированное клиническое исследование ReCharge.JAMA
2014; 312: 915–22. [PubMed] [Google Scholar] 12. Flegal KM, Kit BK, Orpana H, Graubard BI.
Связь общей смертности с избыточной массой тела и ожирением с использованием стандартных категорий индекса массы тела: систематический обзор и метаанализ. JAMA
2013; 309: 71–82. [Бесплатная статья PMC] [PubMed] [Google Scholar] 13. Макдауэлл MA, Fryar CD, Ogden CL, Flegal KM. Справочные антропометрические данные для детей и взрослых: США, 2003-2006 гг. Статистический отчет национального здравоохранения
2008; 10: 1–48. [PubMed] [Google Scholar] 14.Брей Г.А.
Какая идеальная масса тела?
J Nutr Biochem
1998; 9: 489–92. [Google Scholar] 15. Токунага К., Мацузава Ю., Котани К., Кено Ю., Кобатаке Т., Фудзиока С., Таруи С.
Идеальная масса тела по индексу массы тела с наименьшей заболеваемостью. Int J Obes
1991; 15: 1–5. [PubMed] [Google Scholar] 16. Хауэлл WH.
Антропометрия и анализ состава тела. В: Матарезе Л.Е., Готчлих М.М., редакторы. Современная практика поддержки питания: клиническое руководство. Филадельфия: Сондерс, 1998. стр. 33–46. [Google Scholar] 17.Винтер М.А., Гур К.Н., Берг Г.М.
Влияние различной массы тела и концентрации креатинина в сыворотке на систематическую ошибку и точность уравнения Кокрофта-Голта. Фармакотерапия
2012; 32: 604–12. [PubMed] [Google Scholar] Справочные антропометрические данные для детей и взрослых: США, 2003-2006 гг. Статистический отчет национального здравоохранения
2008; 10: 1–48. [PubMed] [Google Scholar] 14.Брей Г.А.
Какая идеальная масса тела?
J Nutr Biochem
1998; 9: 489–92. [Google Scholar] 15. Токунага К., Мацузава Ю., Котани К., Кено Ю., Кобатаке Т., Фудзиока С., Таруи С.
Идеальная масса тела по индексу массы тела с наименьшей заболеваемостью. Int J Obes
1991; 15: 1–5. [PubMed] [Google Scholar] 16. Хауэлл WH.
Антропометрия и анализ состава тела. В: Матарезе Л.Е., Готчлих М.М., редакторы. Современная практика поддержки питания: клиническое руководство. Филадельфия: Сондерс, 1998. стр. 33–46. [Google Scholar] 17.Винтер М.А., Гур К.Н., Берг Г.М.
Влияние различной массы тела и концентрации креатинина в сыворотке на систематическую ошибку и точность уравнения Кокрофта-Голта. Фармакотерапия
2012; 32: 604–12. [PubMed] [Google Scholar]Универсальное уравнение для оценки идеальной массы тела и массы тела при любом ИМТ Am J Clin Nutr. Кортни М. Петерсон2 Лаборатория физиологии скелетных мышц Джона С. Макилхенни и Диана М. Томас4 Центр количественных исследований ожирения, Государственный университет Монклера, Монклер, Нью-Джерси; Джордж Л. Блэкберн5 Центр изучения медицины питания, Медицинский центр Бет Исраэль Дьяконис, Бостон, Массачусетс; и 6 Отдел питания Гарвардской медицинской школы, Бостон, Массачусетс Стивен Б. Хеймсфилд3 Лаборатория метаболизма и состава тела, Центр биомедицинских исследований Пеннингтона, Система государственного университета Луизианы, Батон-Руж, Луизиана; 2 Лаборатория физиологии скелетных мышц Джона С. Макилхенни и 3 Лаборатория метаболизма и состава тела, Центр биомедицинских исследований Пеннингтона, Университет штата Луизиана, Батон-Руж, Луизиана; 4 Центр количественных исследований ожирения, Государственный университет Монклера, Монклер, Нью-Джерси; 5 Центр изучения медицины питания, Медицинский центр диаконис Бет Исраэль, Бостон, Массачусетс; и 6 Отдел питания Гарвардской медицинской школы, Бостон, Массачусетс и Центр трансляционных наук. Поступила 7 августа 2015 г .; Принято 25 февраля 2016 г. Авторские права © Американское общество питания, 2016 г.См. Статью на странице 1193. На эту статью цитировали другие статьи в PMC.AbstractПредпосылки: Уравнения идеальной массы тела (IBW) и диапазоны индекса массы тела (BMI) использовались для определения диапазонов здорового или нормального веса, хотя эти два разных подхода расходятся друг с другом. В частности, прошлые уравнения IBW несовместимы со значениями ИМТ, и, в отличие от ИМТ, в уравнениях не учитывается наличие диапазона идеальной или целевой массы тела. Цель: Впервые, насколько нам известно, мы объединили концепции линейного уравнения IBW и определения целевого веса тела с точки зрения ИМТ. Дизайн: С использованием расчетов и приближений мы получили простое в использовании линейное уравнение, которое врачи могут использовать для расчета как IBW, так и массы тела при любом целевом значении BMI. Результаты: Наше линейное уравнение позволило нам рассчитать массу тела для любого ИМТ и роста со средней эмпирической точностью 0,5–0,7% на основе данных NHANES. Более того, мы показали, что наше уравнение веса тела напрямую согласуется со значениями ИМТ как для мужчин, так и для женщин, что позволяет избежать проблем с переоценкой и недооценкой на верхнем и нижнем концах спектра роста, которые преследовали предыдущие уравнения IBW. Выводы: Наше линейное уравнение увеличивает сложность уравнений IBW, заменяя их одним универсальным уравнением, которое рассчитывает как IBW, так и массу тела при любом целевом ИМТ и росте.Таким образом, наше уравнение совместимо с ИМТ и может применяться с использованием математических вычислений или калькулятора без необходимости в приложении, что делает его полезным инструментом как для практикующих врачей, так и для широкой публики. Ключевые слова: ИМТ, идеальная масса тела, ожирение, избыточный вес, упрощенные уравнения См. Соответствующую редакционную статью на странице 1193. ВВЕДЕНИЕ Как точно определить желаемый или целевой вес тела для оценки питания и здоровья был важным вызов уже более века (1, 2).Многие из первых попыток были основаны на актуарных данных и определяли идеальный или желаемый вес тела с использованием таблиц роста и веса. Поскольку эти таблицы громоздки в использовании, уравнения идеальной массы тела (IBW) для прогнозирования веса как линейной функции от роста были разработаны, начиная с конца 1800-х годов (2). Позже популярность уравнений IBW возросла после того, как Хамви (3) и Девайн (4) опубликовали свои основополагающие уравнения (4). Десять лет спустя, мотивированные приложениями к дозированию лекарств, Robinson et al.(5) и Miller et al. (6) сформулировали уравнения IBW на основе таблиц роста и веса Metropolitan Life Insurance Company 1959 и 1983 годов соответственно. Преимущество уравнений IBW заключается в том, что они предсказывают вес (переменная: Wt) как линейная функция от высоты (переменная: Ht) как , где a — наклон, а b — точка пересечения.Часто термин «рост» выражается как разница от эталонного значения, такого как рост в дюймах, превышающий 5 футов. Например, уравнения Хамви (3) для конкретных полов, разработанные для системы США, оценивают IBW для для мужчин — , а для женщин — , тогда как уравнения Девайна (4) для конкретных полов, которые были разработаны для метрической системы, оценивают IBW для мужчин как , а для женщин как , где Ht выражается в дюймах, а Ht составляет ≥60 дюймов. Однако, несмотря на преимущество простоты, подход IBW имеет 3 важных ограничения. Во-первых, хотя IBW или желаемый вес изначально определялся как вес, связанный с наибольшей ожидаемой продолжительностью жизни на каждом росте, не существует единого идеального веса, универсально применимого ко всем сопутствующим заболеваниям и причинам, связанным со смертностью, и не существует единого идеального веса, который можно было бы использовать. применимо ко всем демографическим факторам, включая возраст и этническую принадлежность (8). Во-вторых, уравнения IBW предсказывают единственную целевую массу тела, тогда как большинство клиницистов предпочитают диапазон целевых масс тела, а эмпирические данные подтверждают это.В-третьих, Shah et al. (2) проанализировали уравнения IBW и показали, что они несовместимы с BMI и, вместо этого, что уравнения IBW занижали массу тела при меньшем росте и завышали массу тела при более высоком росте (2). Напротив, ИМТ, который определяется как масса тела, разделенная на квадрат роста (кг / м 2 ), в настоящее время более широко используется в клинических условиях для диагностики избыточного ожирения и недостаточного веса (9–11).ИМТ имеет два важных преимущества: он позволяет количественно оценить ожирение независимо от роста, и врачи могут использовать ИМТ для определения целевого диапазона веса. Диапазон ИМТ 18,5–24,9 часто рассматривается как диапазон идеального или здорового веса тела [хотя более свежие данные, например, предоставленные Flegal et al. (12) предположили, что несколько более высокие ИМТ связаны с более низкой смертностью], тогда как ИМТ варьируется для статуса избыточного веса (25,0–29,9), ожирения 1 класса (30–34,9; низкий риск), ожирения 2 класса (35.0–39,9; умеренный риск) и ожирение 3 класса (≥40,0; высокий риск) используются для определения риска сопутствующих заболеваний, связанных с ожирением. Эти проблемы приводят к важному вопросу о том, действительно ли уравнения IBW и ИМТ несовместимы или есть способ объединить 2 разных подхода к определению целевого веса тела.Насколько нам известно, впервые мы объединяем концепции уравнения IBW и ИМТ для определения целевого веса тела. Мы показываем, что одно линейное уравнение может оценить как IBW, так и целевую массу тела для любого BMI и роста. В процессе мы показываем, что преимущества уравнений IBW и BMI могут быть объединены в одно простое в использовании уравнение. МЕТОДЫМатематический вывод Хотя концепция ИМТ предсказывает, что вес тела взрослого человека изменяется как криволинейная функция роста (т.е., Wt ∝ Ht 2 ), это соотношение можно оценить с помощью линейного уравнения в пределах 95% диапазона роста населения США (∼60–75 дюймов или ∼1,5–1,9 м) (13). Сначала мы преобразовали уравнение для веса тела как функции роста в форму Затем мы преобразовали уравнение 6 и расширили его до контрольной высоты Ht 0 следующим образом: , где и Ht — это рост человека ().Используя вычислительную технику разложения Тейлора и сохраняя только члены, линейные по ΔHt, мы получили линейное приближение Это приближение оправдано, только если процентная погрешность мала. Поскольку кривая почти линейна в диапазоне высот 95%, процентная погрешность действительно мала (). Здесь процентная погрешность определялась пренебрегаемым членом в разложении в ряд Тейлора Эту погрешность можно вычислить напрямую. Wt почти линейно зависит от Ht. Хотя Wt масштабируется как Ht 2 , Wt является почти линейной функцией Ht в диапазоне 95% Ht (∼1,5–1,9 м). Пример для ИМТ 27 кг / м 2 и показывает эталонный Ht ( Ht 0 ) 1,5 м и Δ Ht , который представляет собой разницу между Ht человека и эталонным Ht 0 . Ht, высота; Вес, вес. Для согласования с предыдущими уравнениями IBW мы выбрали базовую высоту Ht 0 равной 5 футам (60.0 дюймов или 1,52 м) в системе США и 1,5 м (59,1 дюйма) в метрической системе. Однако этот выбор Ht 0 на нижнем конце 95% диапазона высоты вызывал ошибку. Поэтому мы аппроксимировали квадратичный член, показанный в уравнении 10 , компенсирующим линейным членом, который соответствовал весу тела на верхнем конце 95% диапазона роста (75 дюймов или 1,9 м). В нашем выводе было два ключевых шага, которые сделали наш подход превосходящим предыдущие уравнения IBW. Во-первых, найдя выражение для переменной наклона a в уравнении 1 в терминах ИМТ, наше уравнение напрямую согласуется со значениями ИМТ. Такое согласование дает то преимущество, что наше уравнение можно использовать для расчета массы тела при любом целевом значении ИМТ, что, насколько нам известно, никогда раньше не делалось для уравнения IBW. Во-вторых, если выбрать подходящий компенсирующий линейный член (как описано ранее), наше уравнение IBW станет более точным и легко запоминающимся. Сравнительный анализ Мы рассчитали точность выведенного нами уравнения IBW как теоретическими, так и эмпирическими методами. Теоретическая точность рассчитывалась как абсолютная ошибка и процентная погрешность между точным и прогнозируемым весом тела в 95% -ном диапазоне роста (60–75 дюймов или 1,5–1,9 м) при значениях ИМТ 20 и 35. РЕЗУЛЬТАТЫУравнение в системе СШАМы начали с вывода уравнения для системы США.Выведя уравнение, как описано в разделе «Методы», мы преобразовали вес в фунты, а рост в дюймы и расширили его вокруг эталонной высоты 5 футов (60 дюймов), чтобы получить . Затем мы округлили 5,121 до 5 и пренебрегли показанным членом второго порядка. в уравнении 10 . Поскольку пренебрегая этим термином, мы немного занизили вес тела на верхнем конце 95% диапазона роста (ошибка 2,4%), мы нашли линейное приближение для замены члена второго порядка. После выполнения процедуры, изложенной в разделе «Методы», мы обнаружили, что поправочный член для уравнения 10 , необходимый для получения правильного веса на верхнем конце 95% диапазона роста, равен . Клинические примененияЭта легко запоминающаяся формула обеспечивает высокоточный прогноз веса тела при любом целевом ИМТ и росте.Чтобы определить массу тела в фунтах, желаемый ИМТ умножается на 5, а затем прибавляется ИМТ / 5 фунтов на каждый дюйм роста> 5 футов. Например, для ИМТ 20 начните со 100 фунтов на рост 5 футов и добавьте 4 фунта на каждый дополнительный дюйм роста. Для ИМТ 25 начните со 125 фунтов и добавьте 5 фунтов на каждый дюйм роста. Таким образом, выразив наклон через ИМТ, мы разработали уравнение, которое действительно для прогнозирования массы тела при любом заданном ИМТ, что делает его единым универсальным уравнением. В конкретном случае оценки IBW выбирается идеальный BMI для использования в уравнении; этот выбор объединяет концепции уравнений BMI и IBW.Например, если предположить, что ИМТ, равный 20, соответствует ИМТ, наше уравнение предсказывает, что ИМТ будет . и верхнюю границу (25) как . Аналогичным образом, другие диапазоны BMI также могут быть определены с помощью нашего уравнения. показаны расчеты с использованием нашего уравнения при ключевых значениях ИМТ 20, 25, 30, 35, 40, 45 и 50.Каждое увеличение ИМТ на 5 добавляет 25 фунтов к массе тела при росте 5 футов и дополнительно на 1 фунт за каждое увеличение роста на 1 дюйм; этот расчет обеспечивает удобный способ запомнить уравнение, поскольку большинство ключевых значений ИМТ кратны 5. ТАБЛИЦА 1Уравнение массы тела при ключевых значениях ИМТ
Еще одна полезная особенность уравнения состоит в том, что каждое увеличение ИМТ человека на 1 пункт добавляет массы тела. Практический пример, показывающий, как можно использовать это уравнение, можно увидеть в его применении к пациенту с массой тела 225 фунтов и ростом 5 футов 10 дюймов (или 70 дюймов). Если клиницист хочет знать, страдает ли пациент ожирением и какой вес ему необходимо сбросить, чтобы достичь верхнего предела диапазона IBW, быстрый расчет показывает, что вес пациента при ИМТ ожирения 30 составляет , тогда как при верхний предел диапазона здорового ИМТ (<25), пациент будет иметь вес Таким образом, мы классифицируем пациента как страдающего ожирением, и ему или ему нужно будет сбросить 50 фунтов, чтобы считаться нормальным или здоровым диапазон веса. Уравнение в метрической системеДля метрической системы мы использовали ту же математическую процедуру, что и для системы США. Уравнение: , где мы округлили все члены до одного десятичного знака.Для справки: если мы возьмем версию уравнения для США и напрямую переведем ее в метрические единицы, то получим 3,6 вместо 3,5. Однако значение 3,5 дает более низкую совокупную процентную ошибку в диапазоне 95% высоты и, таким образом, является предпочтительным. Точность Наше уравнение очень точное. В, мы проиллюстрировали теоретическую точность нашего уравнения для ИМТ 20 и 35. За исключением высоты ≤61 дюйм (≤1,53 м), уравнение предсказывает правильный вес с точностью до 1 фунта (0. ТАБЛИЦА 2Точность уравнения массы тела 1
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 P = mg – если тело покоится или равномерно движется.
P = mg – если тело покоится или равномерно движется.
 Вес – это сила, измеряемая в ньютонах или килограмм-силах, а не в килограммах. Если вы обсуждаете ваш «вес» с врачом, то вы обсуждаете вашу массу.
Вес – это сила, измеряемая в ньютонах или килограмм-силах, а не в килограммах. Если вы обсуждаете ваш «вес» с врачом, то вы обсуждаете вашу массу. Любопытный факт, касающийся выталкивающей силы: известно, что тело, погруженное в воду, вытесняет объем воды, равный своем весу. Но оно не просто выталкивает воду, тело становится «легче» на объем вытесненной воды. Вот почему поднять в воде девушку массой 60 кг можно шутя и смеясь, а на поверхности это сделать куда сложнее.
Любопытный факт, касающийся выталкивающей силы: известно, что тело, погруженное в воду, вытесняет объем воды, равный своем весу. Но оно не просто выталкивает воду, тело становится «легче» на объем вытесненной воды. Вот почему поднять в воде девушку массой 60 кг можно шутя и смеясь, а на поверхности это сделать куда сложнее.
 Детей интересует буквально всё:-Куда пропадает Солнце…
Детей интересует буквально всё:-Куда пропадает Солнце… Выбор осей определяется соображениями удобства: так, чтобы выражения для проекций законов Ньютона имели бы наиболее простой вид.
Выбор осей определяется соображениями удобства: так, чтобы выражения для проекций законов Ньютона имели бы наиболее простой вид.
 Тело находится в состоянии невесомости, когда оно движется с ускорением свободного падения, то есть когда на него действует только сила тяжести.
Тело находится в состоянии невесомости, когда оно движется с ускорением свободного падения, то есть когда на него действует только сила тяжести. Э. Физика. 10 класс. В 2 ч. Ч 1./Л.Э. Генденштейн, Ю.И. Дик. – М.: Мнемозина, 2009.
Э. Физика. 10 класс. В 2 ч. Ч 1./Л.Э. Генденштейн, Ю.И. Дик. – М.: Мнемозина, 2009. Ускорение нам известно – 9,8 м/с 2 . Осталось найти массу.
Ускорение нам известно – 9,8 м/с 2 . Осталось найти массу. е. ускорение тела равно нулю, вес тела равен силе тяжести.
е. ускорение тела равно нулю, вес тела равен силе тяжести.
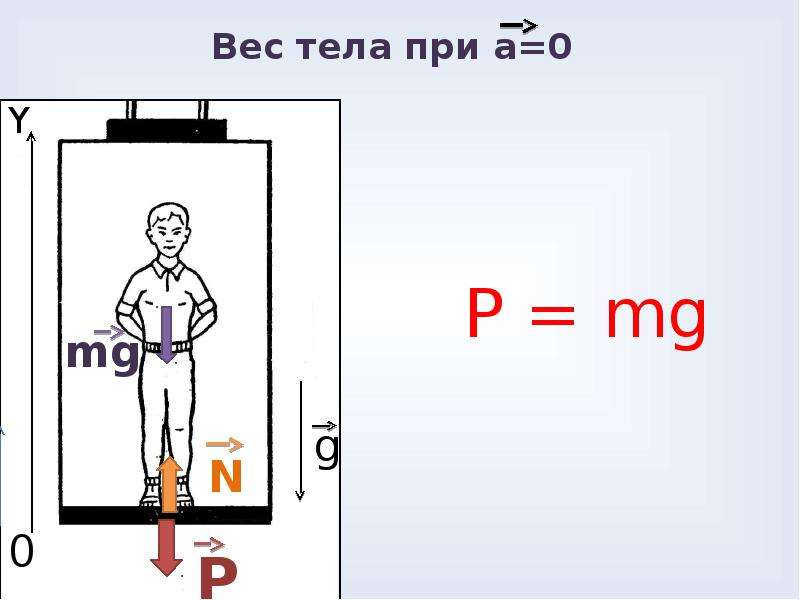 6
6 2
2 89
89 50
50 80
80 89
89 со значениями ИМТ.Как показано в, все остальные уравнения IBW лучше всего соответствовали ИМТ в диапазоне от 21,0 до 24,3. Для сравнения, наше уравнение можно настроить так, чтобы оно соответствовало любому значению ИМТ. Когда мы сравнивали каждое уравнение с наиболее подходящим ИМТ, американская версия нашего уравнения превзошла уравнения IBW, которые оценивали вес тела в фунтах с ошибкой 0,5% для нашего уравнения, по сравнению с ошибками 3,9% и 2,6% для уравнений Хамви ( 3) для мужчин и женщин соответственно. В метрической системе наше уравнение было примерно сопоставимо с уравнением Робинсона и др.(5) для мужчин (ошибка 0,5% по сравнению с ошибкой 0,4%, соответственно), но очень немного превосходит уравнение Робинсона и др. (5) для женщин (ошибка 0,5% по сравнению с ошибкой 0,7%, соответственно). Все другие уравнения IBW, основанные на показателях, не были столь точными и имели ошибки выравнивания ИМТ ≥2,1%.
со значениями ИМТ.Как показано в, все остальные уравнения IBW лучше всего соответствовали ИМТ в диапазоне от 21,0 до 24,3. Для сравнения, наше уравнение можно настроить так, чтобы оно соответствовало любому значению ИМТ. Когда мы сравнивали каждое уравнение с наиболее подходящим ИМТ, американская версия нашего уравнения превзошла уравнения IBW, которые оценивали вес тела в фунтах с ошибкой 0,5% для нашего уравнения, по сравнению с ошибками 3,9% и 2,6% для уравнений Хамви ( 3) для мужчин и женщин соответственно. В метрической системе наше уравнение было примерно сопоставимо с уравнением Робинсона и др.(5) для мужчин (ошибка 0,5% по сравнению с ошибкой 0,4%, соответственно), но очень немного превосходит уравнение Робинсона и др. (5) для женщин (ошибка 0,5% по сравнению с ошибкой 0,7%, соответственно). Все другие уравнения IBW, основанные на показателях, не были столь точными и имели ошибки выравнивания ИМТ ≥2,1%. (текущая статья)
(текущая статья) , 1983 (6)
, 1983 (6) (текущая статья)
(текущая статья) , 1983 (6)
, 1983 (6) Результатом является единое универсальное уравнение, которое описывает массу тела при любом значении ИМТ и росте как в американской, так и в метрической системах. Насколько нам известно, такое уравнение разработано впервые.
Результатом является единое универсальное уравнение, которое описывает массу тела при любом значении ИМТ и росте как в американской, так и в метрической системах. Насколько нам известно, такое уравнение разработано впервые. Во-первых, как было сформулировано ранее, наше уравнение предсказывает массу тела при любом значении ИМТ. Следовательно, его можно использовать для определения диапазона целевых масс тела, как и самих значений ИМТ.Кроме того, если идеальный диапазон ИМТ пересмотрен в сторону увеличения (или уменьшения) или адаптирован к конкретному демографическому результату или результату, зависящему от конкретной причины, наше уравнение по-прежнему остается в силе, поскольку его можно использовать, применяя пересмотренные диапазоны ИМТ. Точно так же наше уравнение может быть адаптировано к цели похудания любого человека, включая более реалистичные целевые значения ИМТ для больных с болезненным ожирением. Эта особенность делает наше уравнение актуальным в широком диапазоне сценариев и приложений.
Во-первых, как было сформулировано ранее, наше уравнение предсказывает массу тела при любом значении ИМТ. Следовательно, его можно использовать для определения диапазона целевых масс тела, как и самих значений ИМТ.Кроме того, если идеальный диапазон ИМТ пересмотрен в сторону увеличения (или уменьшения) или адаптирован к конкретному демографическому результату или результату, зависящему от конкретной причины, наше уравнение по-прежнему остается в силе, поскольку его можно использовать, применяя пересмотренные диапазоны ИМТ. Точно так же наше уравнение может быть адаптировано к цели похудания любого человека, включая более реалистичные целевые значения ИМТ для больных с болезненным ожирением. Эта особенность делает наше уравнение актуальным в широком диапазоне сценариев и приложений. Shah et al. (2) показали, что почти все уравнения IBW недооценивают веса на малых высотах и завышают веса на больших высотах. Чтобы прийти к своим выводам, Shah et al. (2) сравнили уравнения IBW с ИМТ, равным 22,0, что часто подтверждается данными о смертности (14, 15). В данной статье мы применили более сложный подход к измерению соответствия уравнений IBW и BMI.Мы использовали исчисление для вычисления интегрированной процентной ошибки (интегрированное измерение согласования со значениями ИМТ) для 95% диапазона роста и далее нашли значение ИМТ, которое минимизировало процентную ошибку для каждого уравнения IBW. С помощью этого метода мы сравнили каждое уравнение с уникальным ИМТ, которому оно лучше всего подходит. Как показано на, за исключением уравнений IBW Робинсона и др. (5), все уравнения IBW давали ошибки несоосности ≥2,1%. И наше уравнение, и уравнения Робинсона и др. (5) дали наилучшее совпадение со значениями ИМТ (0.Ошибка 4–0,7%). Однако уравнения Робинсона и др. (5) совпадают с разными значениями ИМТ для мужчин и женщин (22,5 для мужчин по сравнению с 21,0 для женщин), тогда как наше уравнение согласуется с одним и тем же ИМТ (выбранным пользователем) для обоих полов.
Shah et al. (2) показали, что почти все уравнения IBW недооценивают веса на малых высотах и завышают веса на больших высотах. Чтобы прийти к своим выводам, Shah et al. (2) сравнили уравнения IBW с ИМТ, равным 22,0, что часто подтверждается данными о смертности (14, 15). В данной статье мы применили более сложный подход к измерению соответствия уравнений IBW и BMI.Мы использовали исчисление для вычисления интегрированной процентной ошибки (интегрированное измерение согласования со значениями ИМТ) для 95% диапазона роста и далее нашли значение ИМТ, которое минимизировало процентную ошибку для каждого уравнения IBW. С помощью этого метода мы сравнили каждое уравнение с уникальным ИМТ, которому оно лучше всего подходит. Как показано на, за исключением уравнений IBW Робинсона и др. (5), все уравнения IBW давали ошибки несоосности ≥2,1%. И наше уравнение, и уравнения Робинсона и др. (5) дали наилучшее совпадение со значениями ИМТ (0.Ошибка 4–0,7%). Однако уравнения Робинсона и др. (5) совпадают с разными значениями ИМТ для мужчин и женщин (22,5 для мужчин по сравнению с 21,0 для женщин), тогда как наше уравнение согласуется с одним и тем же ИМТ (выбранным пользователем) для обоих полов.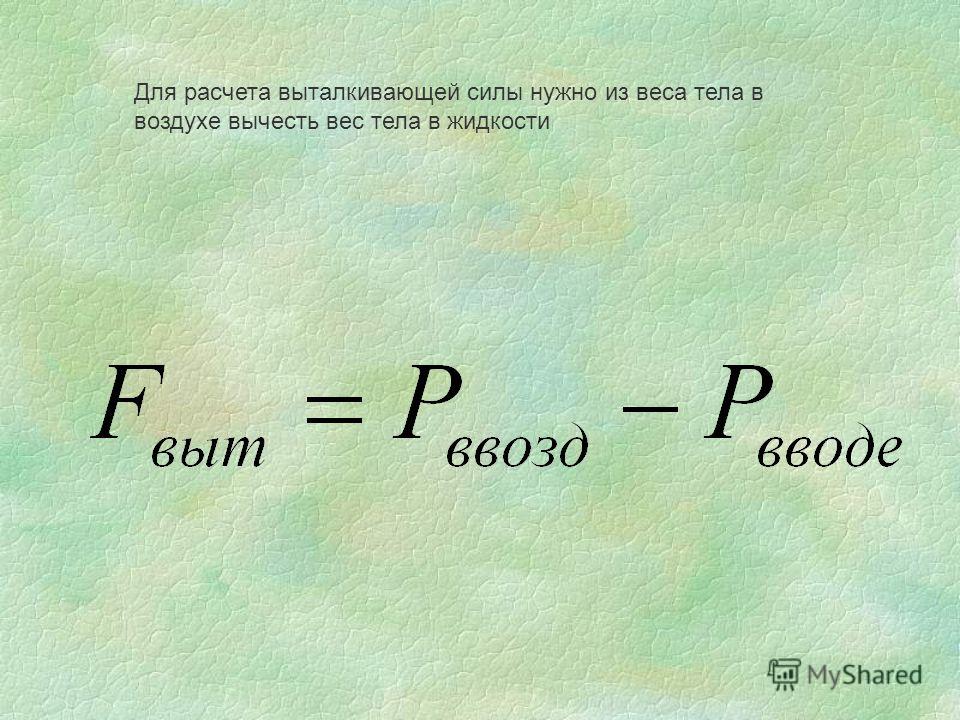 Последней привлекательной особенностью было то, что процентная ошибка для нашего уравнения не зависела от ИМТ и была очень маленькой, в среднем 0,5–0,7% для населения США, по оценке с использованием данных NHANES.
Последней привлекательной особенностью было то, что процентная ошибка для нашего уравнения не зависела от ИМТ и была очень маленькой, в среднем 0,5–0,7% для населения США, по оценке с использованием данных NHANES.

 Ни один из авторов не сообщил о конфликте интересов, связанном с исследованием.
Ни один из авторов не сообщил о конфликте интересов, связанном с исследованием. 2016 May; 103 (5): 1197–1203.
2016 May; 103 (5): 1197–1203.
 Мы измерили эмпирическую точность уравнения с использованием данных NHANES и провели сравнительный анализ с предыдущими уравнениями IBW.
Мы измерили эмпирическую точность уравнения с использованием данных NHANES и провели сравнительный анализ с предыдущими уравнениями IBW.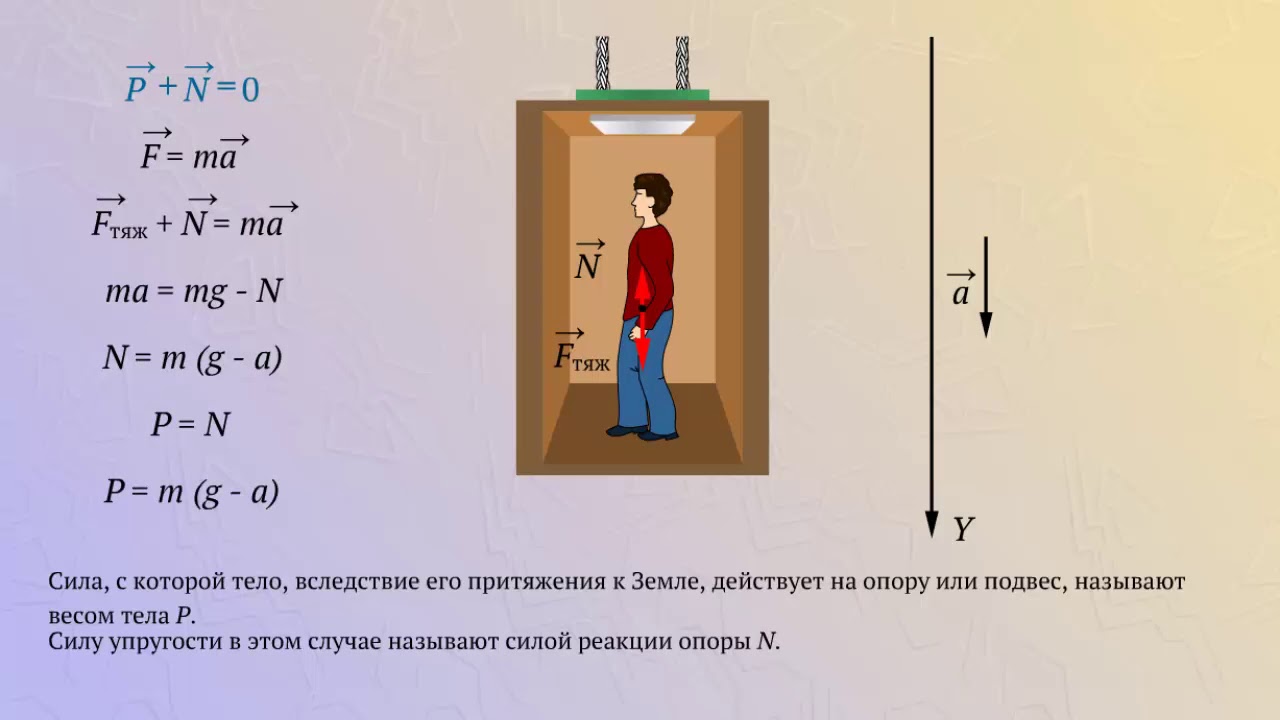
 Совсем недавно Хаммонд (7) создал метрическую версию уравнения Хамви. Хотя уравнения IBW не так популярны, как когда-то, они все еще используются клиницистами для расчета дозировки лекарств, оценки статуса избыточного и недостаточного веса, а также для расчета потребления питательных веществ (2).
Совсем недавно Хаммонд (7) создал метрическую версию уравнения Хамви. Хотя уравнения IBW не так популярны, как когда-то, они все еще используются клиницистами для расчета дозировки лекарств, оценки статуса избыточного и недостаточного веса, а также для расчета потребления питательных веществ (2).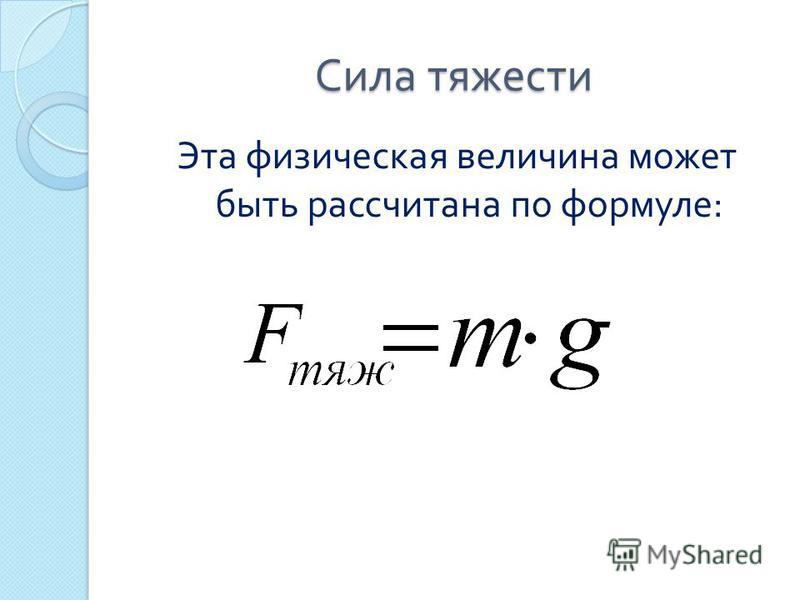 Простая линейная структура этих уравнений позволяет легко вычислить их с помощью мысленной математики или калькулятора.
Простая линейная структура этих уравнений позволяет легко вычислить их с помощью мысленной математики или калькулятора. По этим причинам уравнения IBW в значительной степени были заменены диапазонами BMI.
По этим причинам уравнения IBW в значительной степени были заменены диапазонами BMI. Таким образом, хотя ИМТ сложнее рассчитать, и врачи часто используют приложения для его расчета, этот недостаток обычно перевешивается тем фактом, что можно назначить диапазон целевых весов и что диапазоны более точно связаны с результатами для здоровья.
Таким образом, хотя ИМТ сложнее рассчитать, и врачи часто используют приложения для его расчета, этот недостаток обычно перевешивается тем фактом, что можно назначить диапазон целевых весов и что диапазоны более точно связаны с результатами для здоровья. Однако, в отличие от предыдущих подходов к разработке уравнений IBW, мы строго доказали, что линейная функция верна с использованием исчисления. В процессе мы использовали ключевые этапы вывода, чтобы создать новое уравнение веса тела, которое является более точным, чем предыдущие уравнения IBW, и может быть обобщено на любой ИМТ и рост.
Однако, в отличие от предыдущих подходов к разработке уравнений IBW, мы строго доказали, что линейная функция верна с использованием исчисления. В процессе мы использовали ключевые этапы вывода, чтобы создать новое уравнение веса тела, которое является более точным, чем предыдущие уравнения IBW, и может быть обобщено на любой ИМТ и рост. Например, если эталонная высота находится в середине диапазона высот 95%, максимальная процентная ошибка равна 1.0%.
Например, если эталонная высота находится в середине диапазона высот 95%, максимальная процентная ошибка равна 1.0%.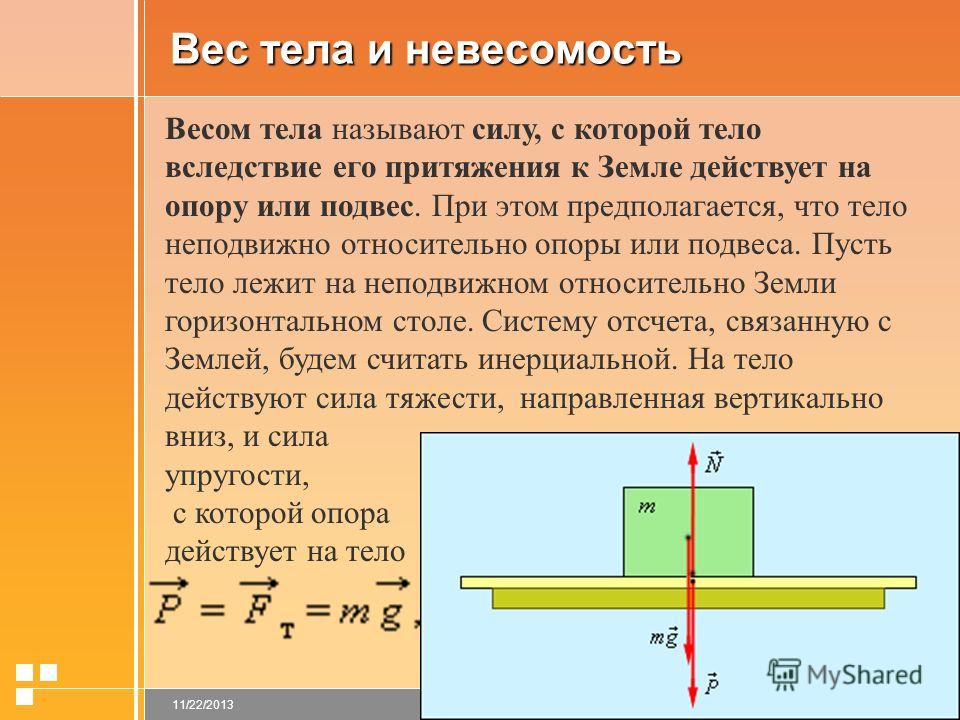 После стратегического округления наше окончательное уравнение было близко к точным касательным и секущим линиям, но дает более точную оценку веса тела, чем любая из этих линий.
После стратегического округления наше окончательное уравнение было близко к точным касательным и секущим линиям, но дает более точную оценку веса тела, чем любая из этих линий. Эмпирическая точность (оба значения: абсолютная ошибка и ошибка в процентах) была рассчитана путем применения нашего уравнения к антропометрическим данным, собранным у взрослых в рамках NHANES 1999–2006 гг.Мы также сравнили, насколько хорошо наше уравнение веса тела и другие уравнения IBW соответствуют значениям ИМТ. Согласование со значениями ИМТ — это один из методов оценки степени соответствия уравнений IBW. Чтобы определить выравнивание, мы использовали программу Mathematica (версия 10.0; Wolfram Research) для вычисления конечного интеграла процентной ошибки каждого уравнения IBW с использованием веса тела, предсказанного ИМТ, в качестве истинного веса. Конечные интегралы были оценены в диапазоне высоты 95% и разделены на разницу между верхней и нижней границами диапазона высоты 95%, чтобы получить среднюю точность.Этот процесс повторяли для каждого значения ИМТ от 17,0 до 27,0 с шагом 0,1, и наименьшее значение средней процентной ошибки в этом диапазоне ИМТ принималось за истинную процентную ошибку для каждого уравнения IBW.
Эмпирическая точность (оба значения: абсолютная ошибка и ошибка в процентах) была рассчитана путем применения нашего уравнения к антропометрическим данным, собранным у взрослых в рамках NHANES 1999–2006 гг.Мы также сравнили, насколько хорошо наше уравнение веса тела и другие уравнения IBW соответствуют значениям ИМТ. Согласование со значениями ИМТ — это один из методов оценки степени соответствия уравнений IBW. Чтобы определить выравнивание, мы использовали программу Mathematica (версия 10.0; Wolfram Research) для вычисления конечного интеграла процентной ошибки каждого уравнения IBW с использованием веса тела, предсказанного ИМТ, в качестве истинного веса. Конечные интегралы были оценены в диапазоне высоты 95% и разделены на разницу между верхней и нижней границами диапазона высоты 95%, чтобы получить среднюю точность.Этот процесс повторяли для каждого значения ИМТ от 17,0 до 27,0 с шагом 0,1, и наименьшее значение средней процентной ошибки в этом диапазоне ИМТ принималось за истинную процентную ошибку для каждого уравнения IBW. Этот метод нахождения наименьшей процентной ошибки правильно учитывает тот факт, что некоторые уравнения IBW согласуются с более высокими ИМТ, тогда как другие уравнения лучше согласуются с более низкими ИМТ и, таким образом, позволяют избежать несправедливого наказания определенных уравнений на этом основании.
Этот метод нахождения наименьшей процентной ошибки правильно учитывает тот факт, что некоторые уравнения IBW согласуются с более высокими ИМТ, тогда как другие уравнения лучше согласуются с более низкими ИМТ и, таким образом, позволяют избежать несправедливого наказания определенных уравнений на этом основании. После того, как этот результат был подставлен обратно в уравнение, мы получили
После того, как этот результат был подставлен обратно в уравнение, мы получили В качестве альтернативы, значения ИМТ в диапазоне от 18,5 до 25,0 могут быть взяты для представления диапазона ИМТ. В этом случае наше уравнение даст нижнюю границу (18,5) для IBW как
В качестве альтернативы, значения ИМТ в диапазоне от 18,5 до 25,0 могут быть взяты для представления диапазона ИМТ. В этом случае наше уравнение даст нижнюю границу (18,5) для IBW как 2 × ИМТ + 3,5 × ИМТ × (Ht — 1,5 м)
2 × ИМТ + 3,5 × ИМТ × (Ht — 1,5 м) Например, каждое увеличение ИМТ на 1 пункт добавляет 6 фунтов массы тела человеку с ростом 5 футов 5 дюймов, 7 фунтов тому, чей рост составляет 5 футов 10 дюймов, и 8 фунтов тому, чей рост составляет 6 футов 3 дюйма. in. Знание о том, что потеря того же постоянного количества фунтов приблизительно снижает ИМТ человека на 1 пункт, может быть полезной и мотивирующей целью для людей, которые пытаются похудеть. И наоборот, при инверсии этого отношения ИМТ человека можно оценить, разделив массу его тела (в фунтах) на 6 фунтов, если рост человека составляет 5 футов 5 дюймов, на 7 фунтов, если рост человека составляет 5 футов 10 дюймов, и на 8 фунтов, если рост человека 6 футов 3 дюйма.Этот метод позволяет человеку быстро оценить ИМТ.
Например, каждое увеличение ИМТ на 1 пункт добавляет 6 фунтов массы тела человеку с ростом 5 футов 5 дюймов, 7 фунтов тому, чей рост составляет 5 футов 10 дюймов, и 8 фунтов тому, чей рост составляет 6 футов 3 дюйма. in. Знание о том, что потеря того же постоянного количества фунтов приблизительно снижает ИМТ человека на 1 пункт, может быть полезной и мотивирующей целью для людей, которые пытаются похудеть. И наоборот, при инверсии этого отношения ИМТ человека можно оценить, разделив массу его тела (в фунтах) на 6 фунтов, если рост человека составляет 5 футов 5 дюймов, на 7 фунтов, если рост человека составляет 5 футов 10 дюймов, и на 8 фунтов, если рост человека 6 футов 3 дюйма.Этот метод позволяет человеку быстро оценить ИМТ. Конечно, для многих пациентов цель по снижению веса на 5–10% может быть более реалистичной, и наше уравнение может учитывать такие персонализированные цели, поскольку оно позволяет оценить массу тела для любого желаемого целевого ИМТ. Например, если ИМТ 28,0 является желаемой целью пациента, целевой вес пациента будет
Конечно, для многих пациентов цель по снижению веса на 5–10% может быть более реалистичной, и наше уравнение может учитывать такие персонализированные цели, поскольку оно позволяет оценить массу тела для любого желаемого целевого ИМТ. Например, если ИМТ 28,0 является желаемой целью пациента, целевой вес пациента будет 5 кг) для ИМТ 20 и с точностью до 2 фунтов (1 кг) для ИМТ 35. Точность нашего уравнения, измеренная с помощью процентной ошибки, не зависит от ИМТ; таким образом, более высокие ИМТ не приводят к большему проценту ошибок. Максимальная процентная погрешность в 95% диапазоне высоты составляет 2,4% для обеих версий уравнения, а уравнение наиболее точное в середине диапазона высот, что является следствием того факта, что оно было разработано таким образом, чтобы минимизировать процентную ошибку. . Наконец, применительно к данным NHANES, наше уравнение дало среднюю эмпирическую точность 0.7% (95% ДИ: 0%, 3,2%) и 0,5% (95% ДИ: 0,3%, 2,4%) для версии США и метрической системы соответственно; это соответствовало средней абсолютной погрешности 1,1 фунта и 0,4 кг соответственно. Ошибка была вызвана в основном людьми с коротким и высоким концом диапазона роста, а влияние ковариат, таких как возраст, было опосредовано лишь косвенно, через их влияние на рост.
5 кг) для ИМТ 20 и с точностью до 2 фунтов (1 кг) для ИМТ 35. Точность нашего уравнения, измеренная с помощью процентной ошибки, не зависит от ИМТ; таким образом, более высокие ИМТ не приводят к большему проценту ошибок. Максимальная процентная погрешность в 95% диапазоне высоты составляет 2,4% для обеих версий уравнения, а уравнение наиболее точное в середине диапазона высот, что является следствием того факта, что оно было разработано таким образом, чтобы минимизировать процентную ошибку. . Наконец, применительно к данным NHANES, наше уравнение дало среднюю эмпирическую точность 0.7% (95% ДИ: 0%, 3,2%) и 0,5% (95% ДИ: 0,3%, 2,4%) для версии США и метрической системы соответственно; это соответствовало средней абсолютной погрешности 1,1 фунта и 0,4 кг соответственно. Ошибка была вызвана в основном людьми с коротким и высоким концом диапазона роста, а влияние ковариат, таких как возраст, было опосредовано лишь косвенно, через их влияние на рост. 50
50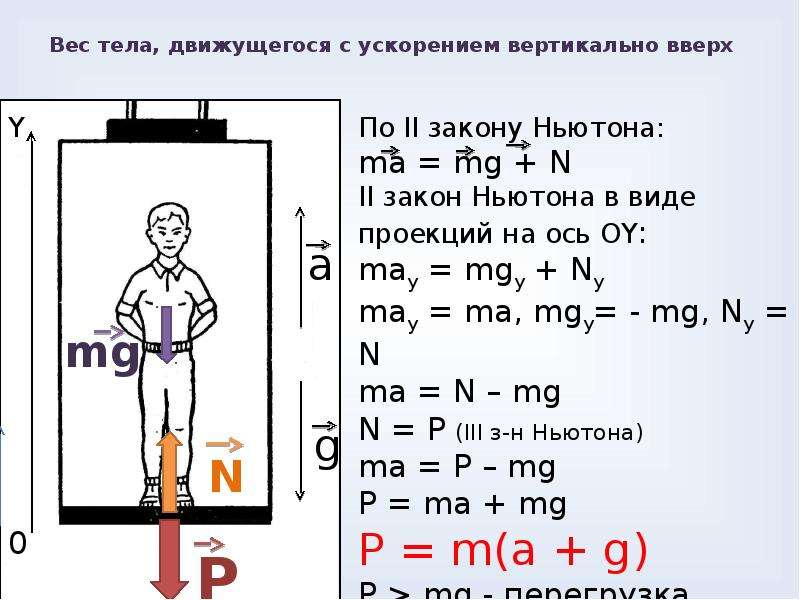 6
6 2
2 89
89 50
50 80
80 89
89 со значениями ИМТ.Как показано в, все остальные уравнения IBW лучше всего соответствовали ИМТ в диапазоне от 21,0 до 24,3. Для сравнения, наше уравнение можно настроить так, чтобы оно соответствовало любому значению ИМТ. Когда мы сравнивали каждое уравнение с наиболее подходящим ИМТ, американская версия нашего уравнения превзошла уравнения IBW, которые оценивали вес тела в фунтах с ошибкой 0,5% для нашего уравнения, по сравнению с ошибками 3,9% и 2,6% для уравнений Хамви ( 3) для мужчин и женщин соответственно. В метрической системе наше уравнение было примерно сопоставимо с уравнением Робинсона и др.(5) для мужчин (ошибка 0,5% по сравнению с ошибкой 0,4%, соответственно), но очень немного превосходит уравнение Робинсона и др. (5) для женщин (ошибка 0,5% по сравнению с ошибкой 0,7%, соответственно). Все другие уравнения IBW, основанные на показателях, не были столь точными и имели ошибки выравнивания ИМТ ≥2,1%.
со значениями ИМТ.Как показано в, все остальные уравнения IBW лучше всего соответствовали ИМТ в диапазоне от 21,0 до 24,3. Для сравнения, наше уравнение можно настроить так, чтобы оно соответствовало любому значению ИМТ. Когда мы сравнивали каждое уравнение с наиболее подходящим ИМТ, американская версия нашего уравнения превзошла уравнения IBW, которые оценивали вес тела в фунтах с ошибкой 0,5% для нашего уравнения, по сравнению с ошибками 3,9% и 2,6% для уравнений Хамви ( 3) для мужчин и женщин соответственно. В метрической системе наше уравнение было примерно сопоставимо с уравнением Робинсона и др.(5) для мужчин (ошибка 0,5% по сравнению с ошибкой 0,4%, соответственно), но очень немного превосходит уравнение Робинсона и др. (5) для женщин (ошибка 0,5% по сравнению с ошибкой 0,7%, соответственно). Все другие уравнения IBW, основанные на показателях, не были столь точными и имели ошибки выравнивания ИМТ ≥2,1%. (текущая статья)
(текущая статья) , 1983 (6)
, 1983 (6) (текущая статья)
(текущая статья) , 1983 (6)
, 1983 (6) Результатом является единое универсальное уравнение, которое описывает массу тела при любом значении ИМТ и росте как в американской, так и в метрической системах. Насколько нам известно, такое уравнение разработано впервые.
Результатом является единое универсальное уравнение, которое описывает массу тела при любом значении ИМТ и росте как в американской, так и в метрической системах. Насколько нам известно, такое уравнение разработано впервые. Во-первых, как было сформулировано ранее, наше уравнение предсказывает массу тела при любом значении ИМТ. Следовательно, его можно использовать для определения диапазона целевых масс тела, как и самих значений ИМТ.Кроме того, если идеальный диапазон ИМТ пересмотрен в сторону увеличения (или уменьшения) или адаптирован к конкретному демографическому результату или результату, зависящему от конкретной причины, наше уравнение по-прежнему остается в силе, поскольку его можно использовать, применяя пересмотренные диапазоны ИМТ. Точно так же наше уравнение может быть адаптировано к цели похудания любого человека, включая более реалистичные целевые значения ИМТ для больных с болезненным ожирением. Эта особенность делает наше уравнение актуальным в широком диапазоне сценариев и приложений.
Во-первых, как было сформулировано ранее, наше уравнение предсказывает массу тела при любом значении ИМТ. Следовательно, его можно использовать для определения диапазона целевых масс тела, как и самих значений ИМТ.Кроме того, если идеальный диапазон ИМТ пересмотрен в сторону увеличения (или уменьшения) или адаптирован к конкретному демографическому результату или результату, зависящему от конкретной причины, наше уравнение по-прежнему остается в силе, поскольку его можно использовать, применяя пересмотренные диапазоны ИМТ. Точно так же наше уравнение может быть адаптировано к цели похудания любого человека, включая более реалистичные целевые значения ИМТ для больных с болезненным ожирением. Эта особенность делает наше уравнение актуальным в широком диапазоне сценариев и приложений. Shah et al. (2) показали, что почти все уравнения IBW недооценивают веса на малых высотах и завышают веса на больших высотах. Чтобы прийти к своим выводам, Shah et al. (2) сравнили уравнения IBW с ИМТ, равным 22,0, что часто подтверждается данными о смертности (14, 15). В данной статье мы применили более сложный подход к измерению соответствия уравнений IBW и BMI.Мы использовали исчисление для вычисления интегрированной процентной ошибки (интегрированное измерение согласования со значениями ИМТ) для 95% диапазона роста и далее нашли значение ИМТ, которое минимизировало процентную ошибку для каждого уравнения IBW. С помощью этого метода мы сравнили каждое уравнение с уникальным ИМТ, которому оно лучше всего подходит. Как показано на, за исключением уравнений IBW Робинсона и др. (5), все уравнения IBW давали ошибки несоосности ≥2,1%. И наше уравнение, и уравнения Робинсона и др. (5) дали наилучшее совпадение со значениями ИМТ (0.Ошибка 4–0,7%). Однако уравнения Робинсона и др. (5) совпадают с разными значениями ИМТ для мужчин и женщин (22,5 для мужчин по сравнению с 21,0 для женщин), тогда как наше уравнение согласуется с одним и тем же ИМТ (выбранным пользователем) для обоих полов.
Shah et al. (2) показали, что почти все уравнения IBW недооценивают веса на малых высотах и завышают веса на больших высотах. Чтобы прийти к своим выводам, Shah et al. (2) сравнили уравнения IBW с ИМТ, равным 22,0, что часто подтверждается данными о смертности (14, 15). В данной статье мы применили более сложный подход к измерению соответствия уравнений IBW и BMI.Мы использовали исчисление для вычисления интегрированной процентной ошибки (интегрированное измерение согласования со значениями ИМТ) для 95% диапазона роста и далее нашли значение ИМТ, которое минимизировало процентную ошибку для каждого уравнения IBW. С помощью этого метода мы сравнили каждое уравнение с уникальным ИМТ, которому оно лучше всего подходит. Как показано на, за исключением уравнений IBW Робинсона и др. (5), все уравнения IBW давали ошибки несоосности ≥2,1%. И наше уравнение, и уравнения Робинсона и др. (5) дали наилучшее совпадение со значениями ИМТ (0.Ошибка 4–0,7%). Однако уравнения Робинсона и др. (5) совпадают с разными значениями ИМТ для мужчин и женщин (22,5 для мужчин по сравнению с 21,0 для женщин), тогда как наше уравнение согласуется с одним и тем же ИМТ (выбранным пользователем) для обоих полов. Последней привлекательной особенностью было то, что процентная ошибка для нашего уравнения не зависела от ИМТ и была очень маленькой, в среднем 0,5–0,7% для населения США, по оценке с использованием данных NHANES.
Последней привлекательной особенностью было то, что процентная ошибка для нашего уравнения не зависела от ИМТ и была очень маленькой, в среднем 0,5–0,7% для населения США, по оценке с использованием данных NHANES.
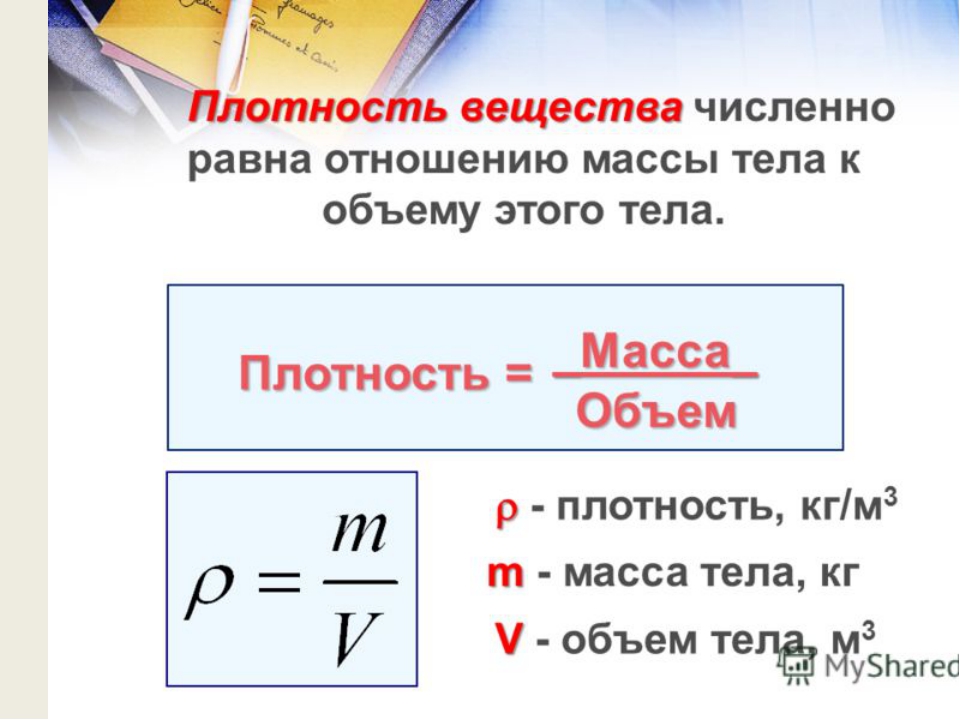
 Ни один из авторов не сообщил о конфликте интересов, связанном с исследованием.
Ни один из авторов не сообщил о конфликте интересов, связанном с исследованием.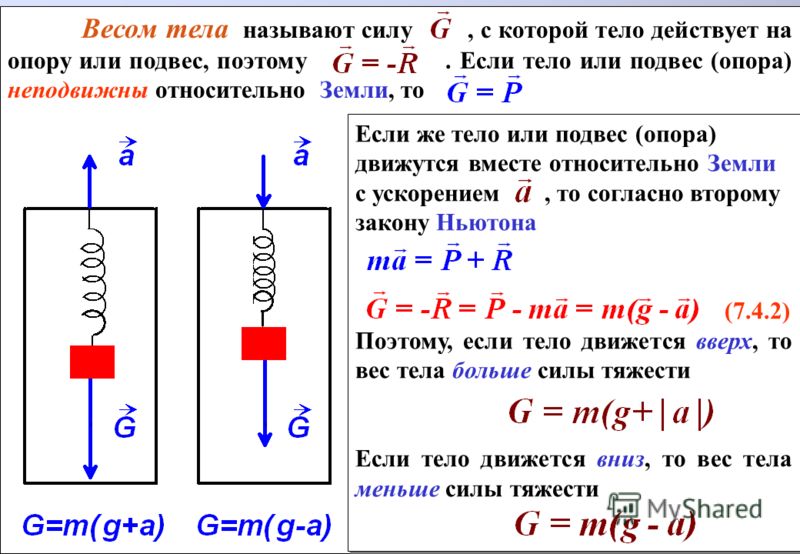 [Google Scholar] 7. Хаммонд К.А.
Диетическая и клиническая оценка.В: Махан Л.К., Пень С.Е., редакторы. Еда, питание и диетотерапия Краузе. 11-е изд.
Филадельфия: Сондерс; 2000. с. 353–79. [Google Scholar] 10. Джин Дж.
Страница пациента JAMA. Лекарства для похудания: показания и применение. JAMA
2015; 313: 2196. [PubMed] [Google Scholar] 11. Икрамуддин С., Блэкстоун Р.П., Бранкатисано А., Тули Дж., Шах С.Н., Вулф Б.М., Фуджиока К., Махер Дж. У., Суэйн Дж., Ку Ф. Г. и др. .
Влияние обратимой прерывистой интраабдоминальной блокады блуждающего нерва на патологическое ожирение: рандомизированное клиническое исследование ReCharge.JAMA
2014; 312: 915–22. [PubMed] [Google Scholar] 12. Flegal KM, Kit BK, Orpana H, Graubard BI.
Связь общей смертности с избыточной массой тела и ожирением с использованием стандартных категорий индекса массы тела: систематический обзор и метаанализ. JAMA
2013; 309: 71–82. [Бесплатная статья PMC] [PubMed] [Google Scholar] 13. Макдауэлл MA, Fryar CD, Ogden CL, Flegal KM.
[Google Scholar] 7. Хаммонд К.А.
Диетическая и клиническая оценка.В: Махан Л.К., Пень С.Е., редакторы. Еда, питание и диетотерапия Краузе. 11-е изд.
Филадельфия: Сондерс; 2000. с. 353–79. [Google Scholar] 10. Джин Дж.
Страница пациента JAMA. Лекарства для похудания: показания и применение. JAMA
2015; 313: 2196. [PubMed] [Google Scholar] 11. Икрамуддин С., Блэкстоун Р.П., Бранкатисано А., Тули Дж., Шах С.Н., Вулф Б.М., Фуджиока К., Махер Дж. У., Суэйн Дж., Ку Ф. Г. и др. .
Влияние обратимой прерывистой интраабдоминальной блокады блуждающего нерва на патологическое ожирение: рандомизированное клиническое исследование ReCharge.JAMA
2014; 312: 915–22. [PubMed] [Google Scholar] 12. Flegal KM, Kit BK, Orpana H, Graubard BI.
Связь общей смертности с избыточной массой тела и ожирением с использованием стандартных категорий индекса массы тела: систематический обзор и метаанализ. JAMA
2013; 309: 71–82. [Бесплатная статья PMC] [PubMed] [Google Scholar] 13. Макдауэлл MA, Fryar CD, Ogden CL, Flegal KM.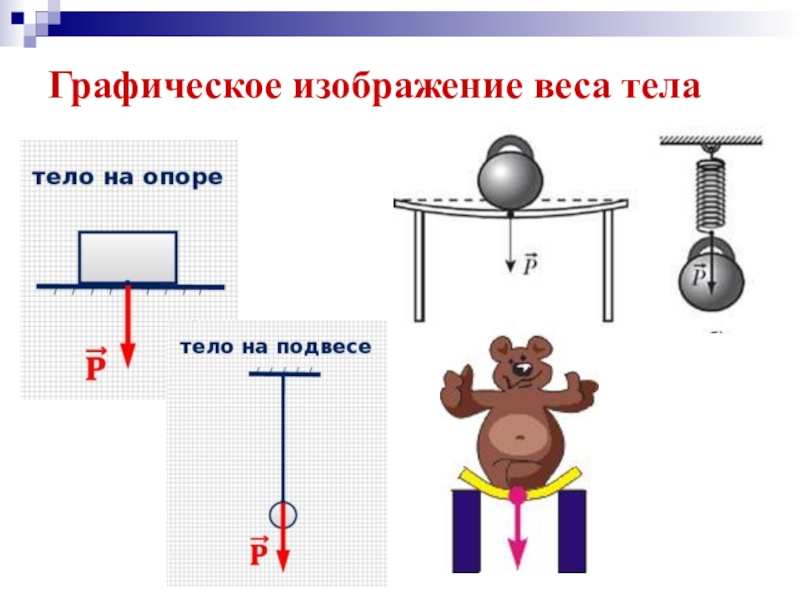 Справочные антропометрические данные для детей и взрослых: США, 2003-2006 гг. Статистический отчет национального здравоохранения
2008; 10: 1–48. [PubMed] [Google Scholar] 14.Брей Г.А.
Какая идеальная масса тела?
J Nutr Biochem
1998; 9: 489–92. [Google Scholar] 15. Токунага К., Мацузава Ю., Котани К., Кено Ю., Кобатаке Т., Фудзиока С., Таруи С.
Идеальная масса тела по индексу массы тела с наименьшей заболеваемостью. Int J Obes
1991; 15: 1–5. [PubMed] [Google Scholar] 16. Хауэлл WH.
Антропометрия и анализ состава тела. В: Матарезе Л.Е., Готчлих М.М., редакторы. Современная практика поддержки питания: клиническое руководство. Филадельфия: Сондерс, 1998. стр. 33–46. [Google Scholar] 17.Винтер М.А., Гур К.Н., Берг Г.М.
Влияние различной массы тела и концентрации креатинина в сыворотке на систематическую ошибку и точность уравнения Кокрофта-Голта. Фармакотерапия
2012; 32: 604–12. [PubMed] [Google Scholar]
Справочные антропометрические данные для детей и взрослых: США, 2003-2006 гг. Статистический отчет национального здравоохранения
2008; 10: 1–48. [PubMed] [Google Scholar] 14.Брей Г.А.
Какая идеальная масса тела?
J Nutr Biochem
1998; 9: 489–92. [Google Scholar] 15. Токунага К., Мацузава Ю., Котани К., Кено Ю., Кобатаке Т., Фудзиока С., Таруи С.
Идеальная масса тела по индексу массы тела с наименьшей заболеваемостью. Int J Obes
1991; 15: 1–5. [PubMed] [Google Scholar] 16. Хауэлл WH.
Антропометрия и анализ состава тела. В: Матарезе Л.Е., Готчлих М.М., редакторы. Современная практика поддержки питания: клиническое руководство. Филадельфия: Сондерс, 1998. стр. 33–46. [Google Scholar] 17.Винтер М.А., Гур К.Н., Берг Г.М.
Влияние различной массы тела и концентрации креатинина в сыворотке на систематическую ошибку и точность уравнения Кокрофта-Голта. Фармакотерапия
2012; 32: 604–12. [PubMed] [Google Scholar]