Типы фигур и способы их коррекции
Какие бывают типы фигур, в чём их особенности, как корректировать и почему многие стилисты не любят сравнивать людей с фруктами? Интересно? Тогда читайте дальше или смотрите видео.
Характеристики типов фигур
Женские фигуры обычно делят на 5 типов: песочные часы, верхний треугольник (клубника), нижний треугольник (груша), прямоугольник (банан), круг (яблоко). В некоторых источников их ещё больше и названия могут немного отличаться. В этой статье мы разберём только пять основных, так как особого смысла делить людей по типам фигур нет. Позже вы узнаете почему.
Песочные часы
Тип фигуры «песочные часы» считается самым идеальным. Плечи и бёдра пропорционально равны, а талия ярко выражена.
Особенности:
- Ширина плеч в плоскости равна ширине бёдер.
- Один размер одежды сверху и снизу.
- Ярко выражена талия. Разница между талией и бёдрами равна или больше 25 см.
- Набранный вес распределяется равномерно по всему телу.
Так как такая фигура считается эталоном, то основная задача при выборе одежды — это подчеркнуть её достоинства и сохранить баланс.
Одежда для фигуры «песочные часы»:
- Выбираем приталенные силуэты либо выделяем талию с помощью ремня.
- Если нет лишнего веса, можно носить облегающую одежду из тонких материалов, если есть, то лучше выбирать более плотные ткани.
- Если большая грудь, лучше не носить свободные топы и платья. Так как не будет видно изгиб тела, будет казаться, что вы толще, чем есть на самом деле.
- Важно понимать, раз фигура «песочные часы» идеально сбалансирована, то с помощью одежды можно легко это нарушить.
 То есть, если вы надеваете объёмный верх, то автоматически становитесь перевернутым треугольником, если объёмный низ, то грушей. Хорошо это или плохо, зависит от ваших вкусов и целей.
То есть, если вы надеваете объёмный верх, то автоматически становитесь перевернутым треугольником, если объёмный низ, то грушей. Хорошо это или плохо, зависит от ваших вкусов и целей.
Прямоугольник
Фигуру «прямоугольник» можно легко найти среди моделей. Ведь она сбалансированная, без ярких изгибов из неё можно построить любой силуэт с помощью одежды.
Особенности:
- Ширина плеч равна ширине бёдер.
- Один размер одежды сверху и снизу.
- Слабо выражена талия.
- Небольшая грудь.
- Вес распределяется равномерно по всему телу.
Так как фигура вся такая ровненькая, хочется добавить линий, объёмов, акцентов. Поэтому красиво будут смотреться глубокие вырезы на топах. Акцент на талии в виде высокой посадки или ремня, поможет показать, что она имеется под одеждой. Объёмный низ сделает фигуру интереснее для взгляда со стороны. А если и талию выделить, и объёма добавить сверху и снизу, то с лёгкостью фигура станет песочными часами.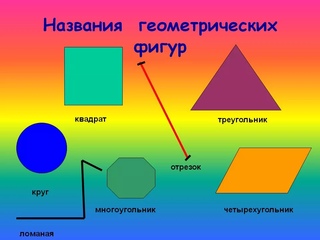
Одежда для фигуры «прямоугольник»
- Акцент на талии (ремень, пояс, высокая посадка).
- Глубокие вырезы.
- Объёмный низ (защипы, карманы, драпировки, рюши, баска и так далее).
- Платья свободного силуэта.
Верхний (перевёрнутый) треугольник
У девушек с фигурой «верхний треугольник» плечи заметно шире бёдер, талия обычно не ярко выражена, но зато красивая грудь и стройные ноги. Мода на одежду с объёмными плечами была в 40-е года, потом в 80-е и сейчас она тоже вернулась. Так что девушки с фигурой перевёрнутый треугольник могут просто добавить объёма вниз с помощью одежды и стать песочными часами или наоборот сделать акцент на плечи и быть в тренде.
Особенности:
- Плечи заметно шире бёдер.
- Слабо выражена талия.
- При наборе веса в первую очередь полнеют руки, грудь, живот.
- Стройные ноги.
- Размер верха часто больше, чем размер низа.

Раз уж считается, что идеально, когда ширина плеч равна ширине бёдер, то вся коррекция направлена на то, чтобы добавить объёма вниз и убрать внимание сверху.
Одежда для фигуры «верхний треугольник»
- V-образные вырезы.
- Рукав реглан или вообще без рукавов.
- Топы с тонкими бретельками.
- Объёмный низ (защипы, карманы, драпировки, рюши, баска и так далее).
- Брюки клёш.
- С помощью цвета: сверху темнее, снизу светлее.
- Отвлекаем внимание: яркие цвета, принты, украшения, аксессуары и тому подобное вниз, а сверху что-то менее заметное.
Нижний треугольник
Фигуру «нижний треугольник» часто называют грушей. Потому что верх меньше низа иногда на несколько размеров, вот и провели такую аналогию. Любимая фигура звёзд хип-хопа. Самые знаменитые «груши» — это Бейонсе, Риана и Ники Минаж. Они не скрывают разницу в пропорциях, а наоборот гордятся своей тонкой талией и большой попой.
Особенности:
- Бёдра заметно шире плеч.
- Ярко выражена талия.
- Размер верха меньше, чем размер низа.
- Небольшая грудь.
- Вес в первую очередь уходит в нижнюю часть тела.
Коррекция фигуры нижний треугольник направлена на то, чтобы сбалансировать верх с низом. То есть добавляем объём в верхнюю часть тела и не акцентируем внимание на нижней.
Одежда для фигуры «нижний треугольник»
- Объёмные рукава, подплечники, рюши и воланы на блузках.
- Вырез лодочкой.
- Акцент на талии.
- Внизу плотные ткани, либо наоборот свободно спадающие вниз.
- Избегать внизу объёмных деталей, ярких цветов, массивных узоров и горизонталей на самом широком месте бедра.
Круг
Такую фигуру ещё часто называют яблоком. Главная особенность в том, что основная доля набранного лишнего веса уходит в живот, но при этом ноги остаются стройными. Наверное, самая известная русская певица с такой фигурой — это Алла Пугачева. Она не просто так любила балахонистые платья, которые всё внимание уводили к стройным ногам.
Наверное, самая известная русская певица с такой фигурой — это Алла Пугачева. Она не просто так любила балахонистые платья, которые всё внимание уводили к стройным ногам.
Особенности:
- Отсутствие талии.
- Один размер верха и низа.
- Стройные ноги.
- Вес в первую очередь уходит в живот.
- Не очень выразительные бёдра.
Так как талии нет, её не надо подчёркивать, девушкам с фигурой круг лучше уводить внимание к стройным ногам.
Одежда для фигуры «нижний треугольник»
- Свободные топы и платья.
- Акцент на стройные ноги.
- Плотные ткани и более прямые силуэты вверху.
Почему многие стилисты не признают типирование фигур?
Современные стилисты говорят, что они не делят людей на фрукты и овощи, что эта система уже устарела. Так почему же типирование фигур считается моветоном?
Самая главная причина — это то, что все мы разные и фигуры у женщин на столько индивидуальны, что редко встретишь чистый «верхний треугольник» или «яблоко». Чаще всего это будут смешанные типы. Например, «песочные часы» стремящиеся к «груше». В справочнике по типам фигур написано, если у вас плечи шире бёдер, стройные ноги, а талия слабо выражена, то вы «верхний треугольник». А в жизни у вас может быть просто плечи широкие, но с талией всё в порядке.
Чаще всего это будут смешанные типы. Например, «песочные часы» стремящиеся к «груше». В справочнике по типам фигур написано, если у вас плечи шире бёдер, стройные ноги, а талия слабо выражена, то вы «верхний треугольник». А в жизни у вас может быть просто плечи широкие, но с талией всё в порядке.
Плюс у каждой девушки есть свои комплексы и предпочтения. Может кого-то вообще не парит, что бёдра шире плеч, а наоборот нравится эта особенность, зачем тогда их скрывать. Сразу вся система ломается. Тем более не все женщины хотят быть «песочными часами». Кто-то просто хочет выглядеть стройнее, выше, менее сексуальной или более. А данная методология не учитывает индивидуальные предпочтения.
Ах, да! Ещё разница в пропорциях бывает такая незначительная, что на неё вообще не стоит обращать внимание и носить то, что хочется.
Поэтому стилисты любят индивидуальный подход к каждому клиенту. Ведь главное, чтобы девушка в одежде чувствовала себя комфортно, чтобы нравилась себе.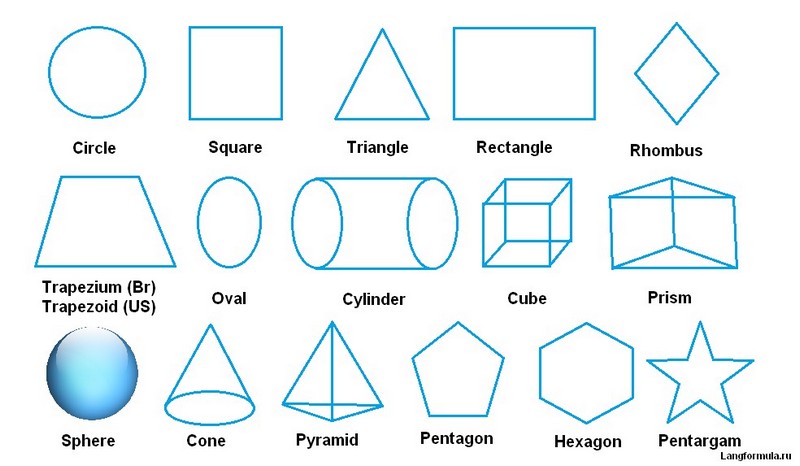
Зачем нужны знания о типах фигур?
- Просто чтобы понимать, о чём речь, если вдруг кто-то назовёт девушку грушей. Или вы, например, где-то увидите информацию для какого-то типа фигуры, то будете хотя бы знать на каких женщин ориентируется автор.
- Если вы считаете, что нет ничего прекраснее идеально сбалансированной фигуры и стремитесь к ней. При этом вы относитесь к одному из вышеперечисленных типов без каких-либо индивидуальных нюансов. Тогда это придумано точно для вас. Смело можете соблюдать все рекомендации для вашего типа фигуры.
- Всем остальным советую внимательно рассмотреть себя в зеркале или на фотографии и понять, что вам нравится, а что нет. Чтобы вы хотели уменьшить, что увеличить, что показать, а что скрыть. Расставить приоритеты и работать с каждым нюансом отдельно. Например, не нравятся широкие бёдра, значит не акцентируем на них внимание и не обтягиваем.
Геометрические фигуры плоские и объёмные
Цели урока:
- Познавательная: создать условия для ознакомления с понятиями плоские и объёмные геометрические фигуры, расширить представление о видах объёмных фигур, научить определять вид фигуры, сравнивать фигуры.

- Коммуникативная: создать условия для формирования умения работать в парах, группах; воспитание доброжелательного отношения друг к другу; воспитывать у учащихся взаимопомощь, взаимовыручку.
- Регулятивная: создать условия для формирования планировать учебную задачу, выстраивать последовательность необходимых операций, корректировать свою деятельность.
- Личностная: создать условия для развития вычислительных навыков, логического мышления, интереса к математике, формирования познавательных интересов, интеллектуальных способностей учащихся, самостоятельность в приобретении новых знаний и практических умений.
Планируемые результаты:
личностные:
- формирование познавательных интересов, интеллектуальных способностей учащихся; формирование ценностных отношений друг к другу;
самостоятельность в приобретении новых знаний и практических умений; - формирование умений воспринимать, перерабатывать полученную информацию, выделять основное содержание.

метапредметные:
- овладение навыками самостоятельного приобретения новых знаний;
- организация учебной деятельности, планирования;
- развитие теоретического мышления на основе формирования умений устанавливать факты.
предметные:
- усвоить понятия плоские и объёмные фигуры, научиться сравнивать фигуры, находить плоские и объёмные фигуры в окружающей действительности, научиться работать с развёрткой.
УУД общенаучные:
- поиск и выделение необходимой информации;
- применение методов информационного поиска, осознанное и произвольное построение речевого высказывания в устной форме.
УУД личностные:
- оценивать свои и чужие поступки;
- проявление доверия, внимательности, доброжелательности;
- умение работать в паре;
- выражать положительное отношение к процессу познания.

Оборудование: учебник, интерактивная доска, смайлики, модели фигур, развёртки фигур, светофоры индивидуальные, прямоугольники -средства обратной связи, Толковый словарь.
Тип урока: изучение нового материала.
Методы: словесные, исследовательские, наглядные, практические.
Формы работы: фронтальная, групповая, парная, индивидуальная.
1. Организация начала урока.
Утром солнышко взошло.
Новый день нам принесло.
Сильными и добрыми
Новый день встречаем мы.
Вот мои руки, я раскрываю
Их навстречу солнцу.
Вот мои ноги, они твердо
Стоят на земле и ведут
Меня верной дорогой.
Вот моя душа, я раскрываю
Её навстречу людям.
Наступи, новый день!
Здравствуй, новый день!
2. Актуализация знаний.
Создадим хорошее настроение. Улыбнитесь мне и друг другу, садитесь!
Чтобы дойти до цели, надо прежде всего идти.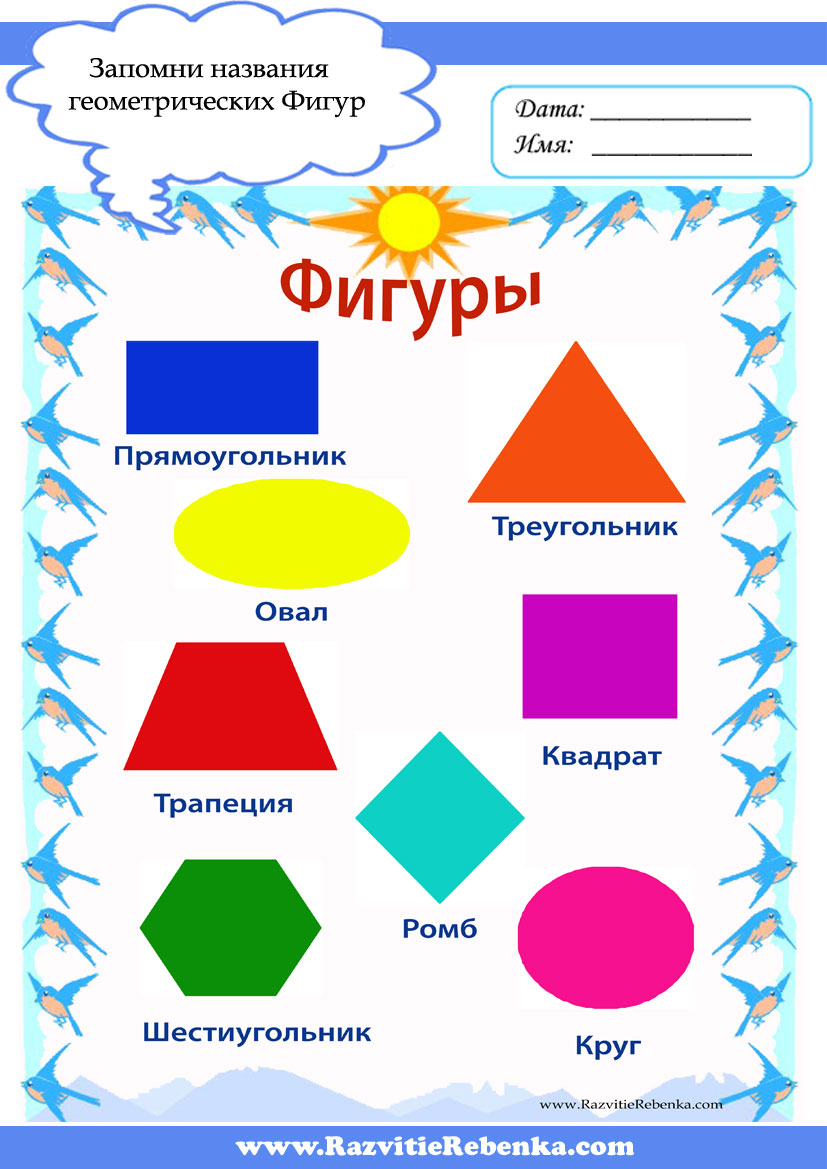
Перед вами высказывание, прочитайте. Что означает это высказывание?
(Чтобы чего-то добиться, нужно что-то делать)
— И действительно, ребята, попадающим в цель может стать только тот, кто настраивает себя на собранность и организованность своих действий. И вот я надеюсь, что мы с вами на уроке достигнем своей цели.
— Начнем наш путь к достижению цели сегодняшнего урока.
3. Подготовительная работа.
— Посмотрите на экран. Что вы видите? (Геометрические фигуры)
Назовите эти фигуры.
— Какое задание, вы можете предложить своим одноклассникам? (разделите фигуры на группы)
— У вас на партах лежат карточки с этими фигурами. Выполните это задание в парах.
— По какому признаку вы разделили эти фигуры?
- Плоские и объемные фигуры
- По основаниям объемных фигур
— С какими фигурами мы уже работали? Что учились находить у них? Какие фигуры встречаются нам на геометрии впервые?
— Какая же тема нашего урока? (Учитель добавляет слова на доске: объёмные, на доске появляется тема урока: Объёмные геометрические фигуры. )
)
— Чему мы должны научиться на уроке?
4. «Открытие» нового знания в практической исследовательской работе.
(Учитель показывает куб и квадрат.)
— Чем они похожи?
— Можно ли сказать, что это одно и тоже?
— Чем же отличается куб от квадрата?
— Давайте проведём опыт. (Ученики получают индивидуальные фигуры – куб и квадрат.)
— Попробуем приложить квадрат к плоской поверхности порты. Что видим? Он весь (целиком) лёг на поверхность парты? Вплотную?
! Как назовём фигуру, которую можно целиком расположить на одной плоской поверхности? (Плоской фигурой.)
— Можно ли куб полностью (весь) прижать к парте? Проверим.
— Можно ли назвать куб плоской фигурой? Почему? Есть ли пространство между рукой и партой?
! Значит, что мы можем сказать о кубе? (Занимает определённое пространство, является объёмной фигурой.)
ВЫВОДЫ: Чем же отличаются плоские и объёмные фигуры? (Учитель вывешивает на доске выводы.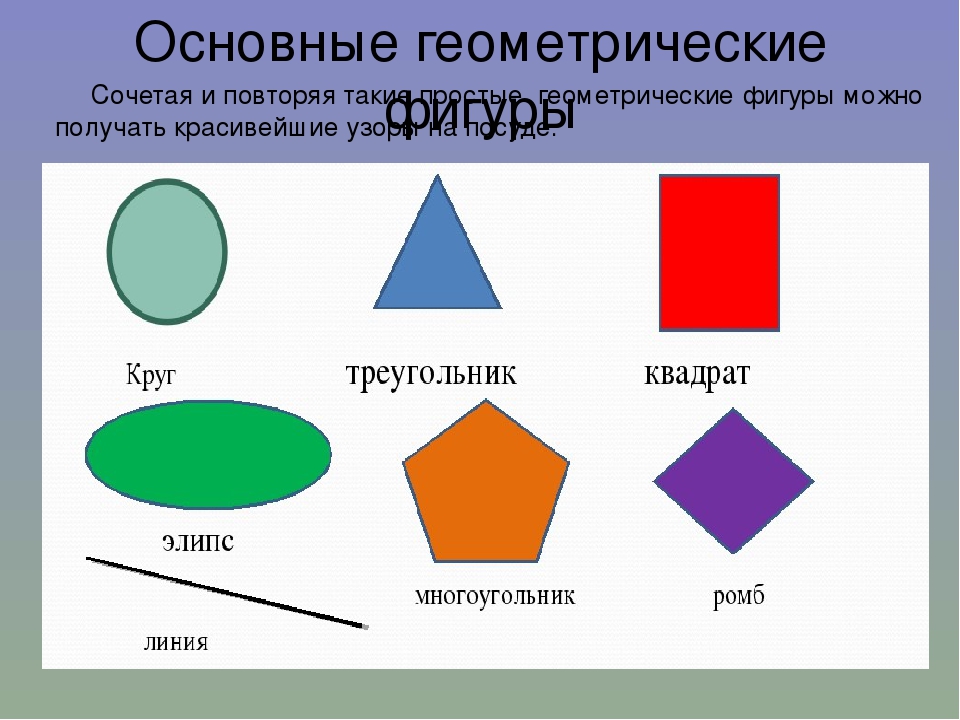 )
)
ПЛОСКИЕ
- Можно целиком расположить на одной плоской поверхности.
ОБЪЁМНЫЕ
- занимают определённое пространство,
- возвышаются над плоской поверхностью.
Объёмные фигуры: пирамида, куб, цилиндр, конус, шар, параллелепипед.
4. Открытие новых знаний.
1. Назовите фигуры, изображенные на рисунке.
— Какую форму имеют основания этих фигур?
— Какие еще формы можно увидеть на поверхности куба и призмы?
2. Фигуры и линии на поверхности объемных фигур имеют свои названия.
— Предложите свои названия.
— Боковые стороны, образующие плоскую фигуру называются гранями. А боковые линии – рёбра. Углы многоугольников – вершины. Это элементы объемных фигур.
— Ребята, а как вы думаете, как называются такие объемные фигуры, у которых много граней? Многогранники.
Работа с тетрадями: чтение нового материала
Соотнесение реальных объектов и объёмных тел.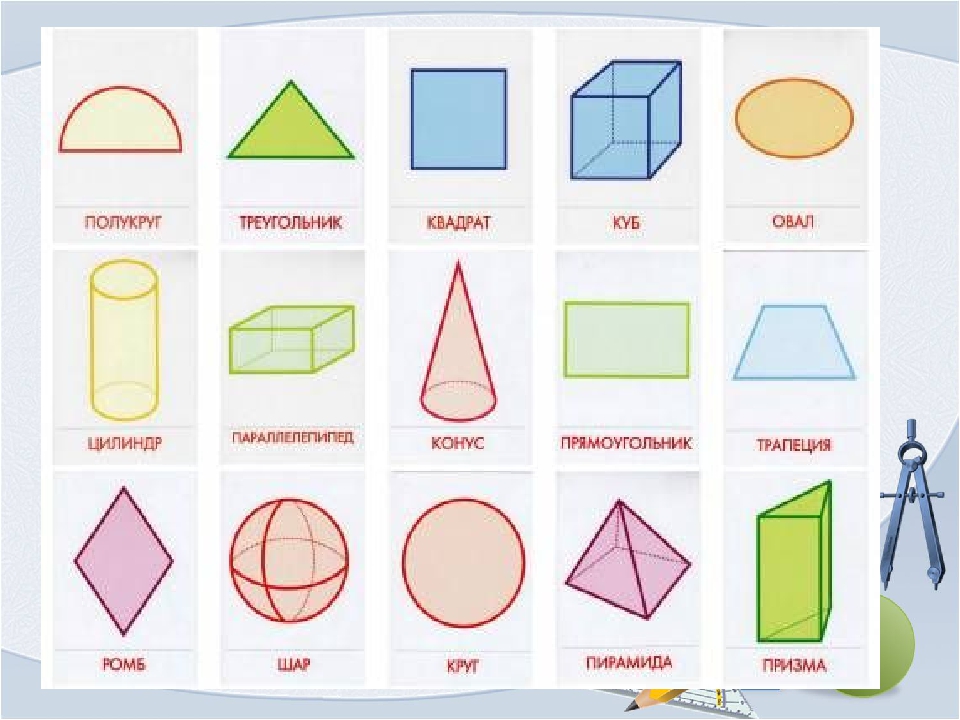
— А теперь подберите для каждого предмета ту объёмную фигуру, на которую он похож.
+ Коробка – параллелепипед.
- Яблоко – шар.
- Пирамидка – пирамида.
- Банка – цилиндр.
- Горшок из-под цветка — конус.
- Колпачок – конус.
- Ваза – цилиндр.
- Мяч – шар.
5. Физминутка.
1. Представьте себе большой шар, погладьте его со всех сторон. Он большой, гладкий.
(Ученики «обхватывают» руками и гладят воображаемый шар.)
А теперь представьте себе конус, дотроньтесь до его вершины. Конус растёт вверх, вот он уже выше вас. Допрыгните до его вершины.
Представьте, что вы внутри цилиндра, похлопайте по его верхнему основанию, потопайте по нижнему, а теперь руками по боковой поверхности.
Цилиндр стал маленькой подарочной коробочкой. Представьте, что вы сюрприз, который находится в этой коробочке. Я нажимаю кнопку и… сюрприз выскакивает из коробочки!
6.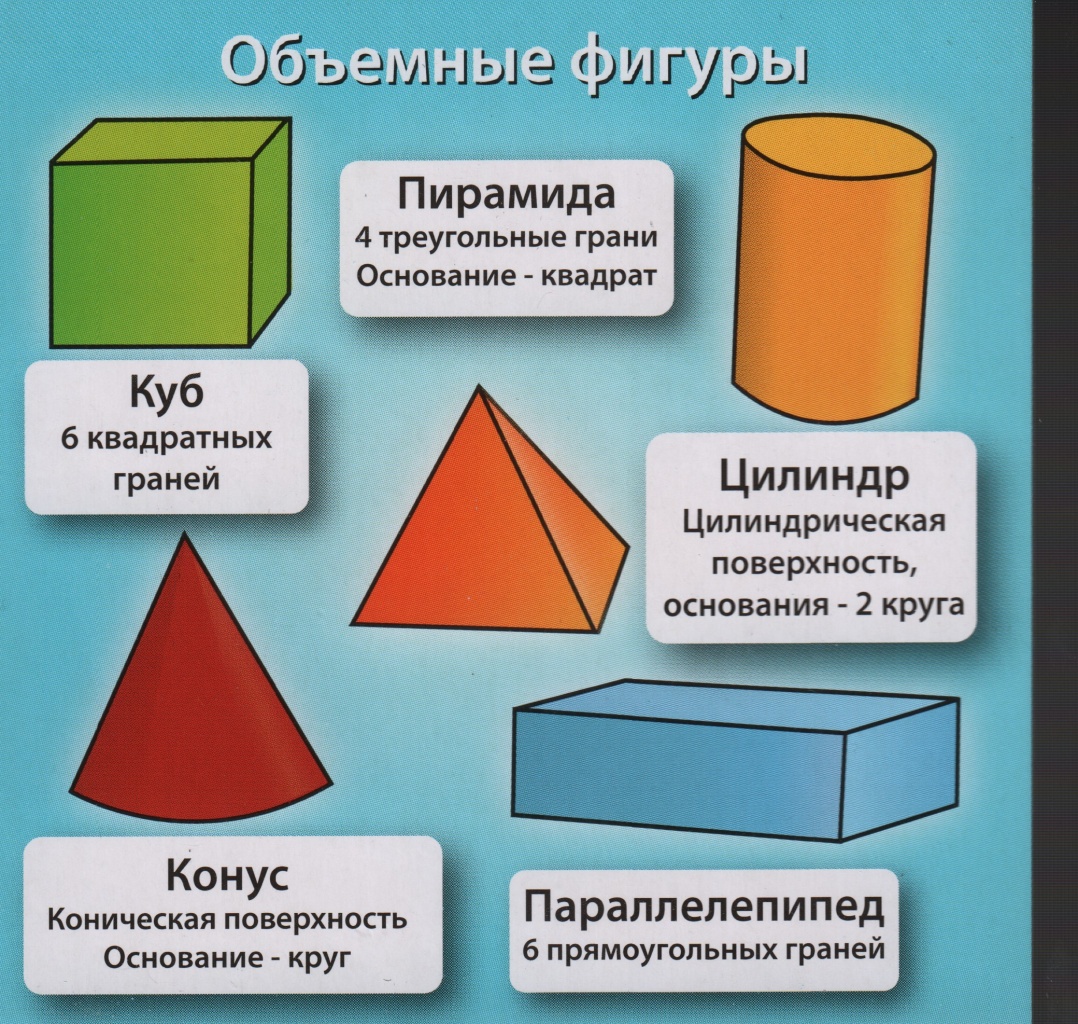 Групповая работа:
Групповая работа:
(Каждая группа получает одну из фигур: куб, пирамиду, параллелепипед.Полученную фигуру дети изучают, выводы записывают в подготовленную учителем карточку.)
Группа 1. (Для изучения параллелепипеда)
| Эта объемная фигура называется ______________ . Его стороны (грани) похожи на плоскую фигуру ______________ . Их ровно ______________ . Еще у этой фигуры есть углы – вершины, их ______________ . |
Группа 2. (Для изучения пирамиды)
| Эта объемная фигура называется ______________ . Его стороны (грани) похожи на плоскую фигуру ______________ . Их ровно ______________ . Еще у этой фигуры есть углы – вершины, их ______________ . |
Группа 3. (Для изучения куба)
Эта объемная фигура называется ______________ .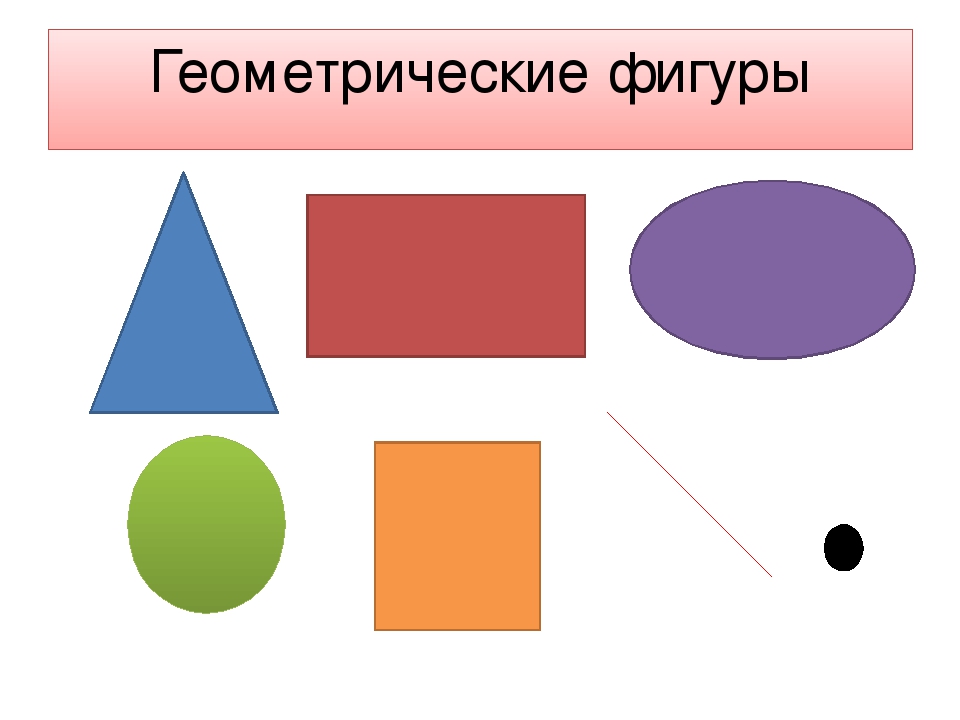 Его стороны (грани) похожи на плоскую фигуру ______________ . Их ровно ______________ . Еще у этой фигуры есть углы – вершины, их ______________ . |
Далее каждая группа выступает, представляя свою объемную фигуру другим.
7. Решение кроссворда
8. Итог урока. Рефлексия деятельности.
Решение кроссворда в презентации
— Что нового вы для себя сегодня открыли?
+ Все геометрические фигуры можно разделить на объёмные и плоские.
+ А я узнал названия объёмных фигур
Управление фигурами в Visio для Интернета
В Веб-приложение Visio есть множество фигур, которые объединены в наборы. Создание любой схемы можно начать с набора фигур. Однако можно также добавить наборы фигур на палитру для быстрого доступа. Например, чтобы создать схему процесса, можно добавить набор фигур простой блок-схемы.
Используйте палитру фигур для добавления, просмотра и удаления наборов фигур.
Добавление набора фигур
-
Откройте схему для редактирования.
-
В области табуляции (видимой на левом поле на рисунке выше) выберите команду Добавить фигуры .
-
Прокрутите список наборов фигур, чтобы увидеть все доступные варианты.
-
Чтобы отобразить доступные фигуры в наборе, выберите элемент Просмотр .
-
Чтобы добавить набор фигур, выберите команду Добавить.
Просмотр добавленного набора фигур
Набор фигур, который вы добавили, может отобразиться не сразу.
-
Откройте схему для редактирования.
-
В области вкладок выберите значок набора фигур.
 При наведении указателя мыши на значок появляется название набора.
При наведении указателя мыши на значок появляется название набора.
Удаление набора фигур
Для очистки палитры фигур может потребоваться удалить наборы. Вы всегда сможете вернуть их на место позже.
-
Откройте схему для редактирования.
-
В области вкладок фигур щелкните правой кнопкой мыши значок набора фигур и выберите пункт Удалить.
К началу страницы
См. также
Справка по Visio для веба
Просмотр, создание и изменение схем в Visio для веб-сайта.
Выделение, копирование и перемещение фигур в Visio для Интернета
Изменение размера, угла поворота и порядка фигур в Visio для веб-сайта
Список различных типов геометрических фигур с картинками
Мы встречаем различные типы объектов и материалов, которые коренным образом регулируются конкретные геометрические аспекты, которые делают их появляются уникальными в собственном образе. Это бизнес сайт статья даст вам исчерпывающую информацию о различных видах и названия геометрических фигур, вместе с их значениями и цены. Быстрый Факт
Это бизнес сайт статья даст вам исчерпывающую информацию о различных видах и названия геометрических фигур, вместе с их значениями и цены. Быстрый Факт
Как сообщается, в области геометрии и связанного с изучением формы и фигуры возник первый в реки Инда цивилизации и Вавилонской цивилизации около 3000 до н. э.. Некоторые отчеты показывают, что у египтян была своя версия теоремы Пифагора даже перед Пифагор сформулировал это. Внешний вид или форма предмета или тела, которое остается стабильным или постоянным при определенных нормальных условиях называется геометрической формы объекта. Проще говоря, геометрические фигуры характеризуются как внешние ориентации рассматриваемых объектов. В качестве параметров отличаются, так что типы формы. Если фигуры двух объектов одинаковые или похожие, они равны друг другу. Любого известного тела или материалистической сущности во всей Вселенной, можно сказать, присутствует в виде геометрической формы.
— Добавление Показателей
В основном существует два вида геометрических фигур: двухмерные (2D) и трехмерного (3D). Первые могут быть сделаны со ссылкой на оси X и Y, в то время как последний также включает в себя ось Z. 2D формы и фигуры в основном состоят из точек и соединяющих линий, которые образуют форму. Они могут быть либо выпуклой (обычный вид) или вогнутая (нерегулярные) внешний вид. Во многих полигональных 2Д фигуры, выпуклые, имеют углы меньше 180 градусов, в то время как вогнутые формы имеют хотя бы один угол больше 180 градусов. 3D-фигуры более сложные, и состоят в основном из вершин, ребер, граней и т. д..
Первые могут быть сделаны со ссылкой на оси X и Y, в то время как последний также включает в себя ось Z. 2D формы и фигуры в основном состоят из точек и соединяющих линий, которые образуют форму. Они могут быть либо выпуклой (обычный вид) или вогнутая (нерегулярные) внешний вид. Во многих полигональных 2Д фигуры, выпуклые, имеют углы меньше 180 градусов, в то время как вогнутые формы имеют хотя бы один угол больше 180 градусов. 3D-фигуры более сложные, и состоят в основном из вершин, ребер, граней и т. д..
— Как использовать научный калькулятор
Индекс
Двух мерное (2D) формы
■ треугольники
■ Четырехугольники
■ полигоны
■ Криволинейной Формы
Трехмерная (3D) фигуры
Следующие разделы помогут вам понять значение основных геометрических фигур, а также их фотографии. Обратите внимание, что все указанные углы являются внутренними.
Различные типы геометрических фигур
Двух мерное (2D) формы
Треугольники
Это типа полигон, который состоит из трех сторон с тремя апексами. Сумма углов треугольника равна 180 градусов в любом типе. Смотрите раздел ниже для более подробной информации.
Сумма углов треугольника равна 180 градусов в любом типе. Смотрите раздел ниже для более подробной информации.
Равнобедренный Треугольник
Две стороны равны и два угла тоже равны. Линия симметрии присутствует. Треугольник Разносторонний
Длины всех сторон равны, и всех трех углов имеют разные значения.
Равносторонний Треугольник
Все три стороны и углы равны. Линия симметрии присутствует. Прямоугольный Треугольник
Один из углов 90 градусов. Линия симметрии может и не быть.
Тупоугольному Треугольнику
Один из углов больше 90 градусов. Линия симметрии может и не быть. Острый Треугольник
Все углы острые (меньше 90 градусов). Линия симметрии может и не быть. Обратно в индекс
Четырехугольники
Эти полигоны состоят из четырех сторон, и сумма углов равна 360 градусов в любом типе. Смотрите раздел ниже для более подробной информации.
Прямоугольник
У них есть две пары противоположных сторон равны и все четыре угла 90 градусов. Две линии симметрии присутствуют. Площадь
Две линии симметрии присутствуют. Площадь
Все четыре угла равны 90 градусов, вместе с четырьмя равными сторонами. Этот многоугольник имеет четыре линии симметрии.
Параллелограмм
Они состоят из двух наборов противоположных линий, которые равны и параллельны. Противоположные углы также равны по любой стоимости. Линия симметрии может присутствовать. Ромб
Все четыре стороны равны и параллельны, но только противоположные углы равны. Две линии симметрии присутствуют. Она тесно связана с квадрат и параллелограмм. Обратно в индекс
Трапециевидные
Один набор противоположные линии параллельна и другой набор непараллельных. Линия симметрии может присутствовать. Это называется трапеция в Великобритании.
Трапецеидальная
Все четыре стороны не равны и не параллельны, а линии симметрии отсутствует. Это называется Трапецией в Великобритании.
Кайт
Две пары смежных сторон равны и два противоположных угла имеют равные значения. Линия симметрии присутствует. Нерегулярные Четырехугольник
Линия симметрии присутствует. Нерегулярные Четырехугольник
Она имеет четыре неравные стороны, и появление вогнутая, я. э. по крайней мере один угол больше 180 градусов. Обратно в индекс
Полигоны
Цифры, которые состоят из трех или более чем трех сторон известны как многоугольники. Углы в таких геометрических фигур может быть больше, чем 360 градусов. Как регулярные, так и нерегулярные типы полигонов приведены ниже.
Примечание: хотя треугольник и четырехугольник включены под полигоны, как они были описаны выше, они не перечислены в следующем разделе.
Пентагон
Он состоит из пяти равных сторон, и сумма углов равна 540 градусов. Пять линий симметрии присутствуют. Шестигранник
Он состоит из шести равных сторон, и сумма углов равна 720 градусов. Шесть осей симметрии присутствуют.
Семиугольник
Он состоит из семи равных сторон, и сумма углов равна 900 градусов. Семь линий симметрии присутствуют. Восьмиугольник
Она состоит из восьми равных сторон, и сумма углов равна 1080 градусов. Восемь линий симметрии присутствуют. Обратно в индекс
Восемь линий симметрии присутствуют. Обратно в индекс
Девятиугольника
Она состоит из девяти равных сторон, и сумма углов равна 1260 градусов. Девять линий симметрии присутствуют. Декагон
Он состоит из десяти равных сторон, и сумма углов равна 1440 градусов. Десять линий симметрии присутствуют.
Двенадцатиугольник
Он состоит из двенадцати равных сторон, и сумма углов равна 1800 градусов. Двенадцать линий симметрии присутствуют. Неправильного Многоугольника
Он может иметь четыре и более неравных сторон, а внешний вид может быть вогнутой, я. э. по крайней мере один угол больше 180 градусов. Обратно в индекс
Изогнутые Формы
Фигуры, состоящие из кривых линий и соответствующие точки называются криволинейной формы. Основные виды, которые входят в эту категорию можно отнести следующие:
Круг
Состоящая только из одной изогнутой линии, эта форма не имеет какой-либо другой точки присоединения или Apex. Расстояние от эпицентра до окружности равны во всех отраслях. Овал/Эллипс
Овал/Эллипс
Он похож на круг, но расстояние от центра до окружности постоянно изменяется. Таким образом, эта форма имеет две оси: крупных и мелких, вместе с вытянутую форму.
Объектив
Эта цифра похожа на эллипс, но состоит из двух отдельных изогнутых линий, которые встретятся на противоположных концах. В данном случае, присутствуют две точки на их стыке. Полумесяц
Эта форма характеризуется наличием двух изогнутых линий: одна выпуклая, а другая вогнутая. Они встречаются в подобной манере, как линзы, образуя своеобразный рисунок. Обратно в индекс
Арки
Эти цифры состоят из изогнутых линий, что соответствует прямой линии в двух соседних точек. Бывшая линия может быть полностью изогнутым или может быть в виде двух параллельных линий до вступления в прямой линии. Кольца
Этот показатель характеризуется наличием двух концентрических кольцевых структур, которые отличаются по размеру. В большинстве случаев, интерьер форма не закрывается. Этот показатель также называют кольцевую структуру.
Этот показатель также называют кольцевую структуру.
Круговой Сегмент
Это, главным образом, определяется как часть окружности, которая может представлять собой часть окружности, вместе с хордой. Форма может быть полукруг или может быть фигура с минимальной части окружности. Оставшуюся часть также можно назвать сегмент. Круговой Сектор
Это, главным образом, определяется как треугольный участок, который обозначен частью круговой окружность и две прямые линии. Последние встречаются в общей точке, в основном в Центральном круге. Они оставшуюся половину круга также можно назвать сектор. Обратно в индекс
Формы, описанные выше, являются основными, а кроме них, существуют и многие другие деятели в категории 2D геометрии. Пройдя через эти формы, давайте взглянем на различные виды геометрических фигур, которые подпадают под 3 категории.
Трехмерная (3D) фигуры
Куб/Шестигранник
Этот показатель имеет 12 ребер, 8 вершин и 6 граней. Стороны все равны в длину и лица квадратной формы. Прямоугольная Призма/Прямоугольный Параллелепипед
Прямоугольная Призма/Прямоугольный Параллелепипед
Он имеет те же функции, что Куба по количеству сторон, граней и вершин, за исключением того, что лица имеют прямоугольную форму.
Цилиндр
Эта форма не имеет каких-либо вершин, но состоит из двух плоских граней (только в случае закрытого цилиндра), и одним кривым лицом. Два ребра присутствуют. Сфера
Эта Геометрическая фигура не имеет каких-либо ребер и вершин, и только одна изогнутая лицо присутствует. Это наиболее равномерно изогнутые формы включены в категории 3D. Обратно в индекс
Треугольная Призма
Он состоит из шести вершин, девять краев, и пять лиц. Лица на обоих концах треугольной формы, тогда как все остальные имеют прямоугольную форму. Конусная
Вместе с одной вершиной и одной из кромок, конусов, один кривым лицом, и одной дополнительной плоской грани (в закрытых шишек). Угол вершины может варьироваться от острой до тупой.
Шестиугольная Призма
Состоящий из двенадцати вершин, ребер восемнадцать, и восемь лиц, эта цифра имеет два шестигранники на противоположных концах. Остальные грани имеют прямоугольную или квадратную форму. Пятиугольная Призма
Остальные грани имеют прямоугольную или квадратную форму. Пятиугольная Призма
Состоящий из десяти вершин, ребер пятнадцать, и семь лиц, эта цифра имеет двух пятиугольников на противоположных концах. Остальные грани имеют прямоугольную или квадратную форму. Обратно в индекс
Квадратная Пирамида
В таком виде база состоит из квадрата, а остальные грани треугольники. В целом, он имеет 5 вершин, 8 ребер и 5 граней. Треугольная Пирамида
В этой формы, базу, а также все грани треугольники. В целом, он имеет 4 вершины, 6 ребер и 4 грани. Базальный треугольник имеет разный размер по сравнению с лицами.
Шестиугольная Пирамида
Эта форма в основном состоит из 7 вершин, 12 ребер и граней 7. Его основание шестиугольной формы, и грани треугольные.
Параллелепипед
На этом рисунке все грани и основание имеют форму параллелограммов. Размеры граней могут отличаться или могут быть одинаковые. Обратно в индекс
Тетраэдр
Это похоже на появление треугольной пирамиды, с тем лишь исключением, что все грани и основание всех одинакового размера. Октаэдр
Октаэдр
Этот показатель имеет восемь треугольников, расположенных в определенном порядке, чтобы сформировать шесть вершин, восемь граней, двенадцать ребер. Треугольники могут быть равносторонними или равнобедренными.
Додекаэдр
Они состоят из двенадцати пятиугольников, двадцать вершин и 30 ребер. Лица имеют равные пятиугольники.
Икосаэдр
Они характеризуются 30 ребер, 20 граней и 12 вершин. Лица состоят из равносторонних треугольников. Обратно в индекс
Ромбический Додекаэдр
Этот тип фигуры состоит из 12 ромбовидная лица, вместе с 14 вершин и 24 ребра.
Усеченный
Он представляет собой конусообразную конструкцию, но вместо Апекс, круг присутствует на одном конце.
Всестороннее знание геометрических фигур и рисунков очень важно, особенно если есть склонность к этой суб-области математики. Кроме того, человек должен научиться следовать разные математические правила, необходимые при рисовании геометрических фигур. Фигуры, описанные выше, вместе с образцом уравнений, несомненно, поможет вам очистить свои основы о этой теме.
Комментарии
— 27.12.2020 09:33:50
— 06.02.2020 10:15:11
— 17.09.2019 18:52:46
— 16.01.2019 22:04:13
ПЕТЯ — 12.03.2018 23:14:10
ГДЕ НАЗВАНИЯ ФИГУР
как выбрать одежду по типу фигуры
Мои ноги вовсе не так красивы, как вы думаете, — просто я знаю, что с ними делать! /Марлен Дитрих/
КАК ВЫБРАТЬ ОДЕЖДУ ПО ТИПУ ФИГУРЫ
Не спешите отчаиваться и не драматизируйте, если параметры вашей фигуры далеки от модельных 90-60-90 см, или если вы как и любая девушка всю жизнь о таких мечтаете. Все возможно в нашем мире! Из любой ситуации находится выход, когда его ищут особо внимательно. Главное любите себя такими, как Вы есть! А чтобы выглядеть на 100%, корректируйте свой облик одеждой по типу вашей шикарной фигуры и наслаждайтесь собой и жизнью…
Ведь, все знают звезд, фигуры которых не стандартны, следовательно не идеальны. А вот, что для кого идеал, всегда остается загадкой. Некоторые мужчины выбирают любимых с «сочными» формами, и для них избранница это идеал красоты (женщина же в большинстве случаев для любимого старается), некоторым нравятся худые. Но, знайте, что прекрасная внешняя форма — это не панацея, тут дело в другом. Вы должны уметь подчеркивать свои достоинства и научиться вуалировать недостатки. Советуем впреть подходить к шоппингу ответственно и проанализировать к какому типу фигуры соответствует Ваша, так Вам легче будет создать привлекательный женственный образ с помощью платья по типу фигуры или стильного костюма.
Некоторые мужчины выбирают любимых с «сочными» формами, и для них избранница это идеал красоты (женщина же в большинстве случаев для любимого старается), некоторым нравятся худые. Но, знайте, что прекрасная внешняя форма — это не панацея, тут дело в другом. Вы должны уметь подчеркивать свои достоинства и научиться вуалировать недостатки. Советуем впреть подходить к шоппингу ответственно и проанализировать к какому типу фигуры соответствует Ваша, так Вам легче будет создать привлекательный женственный образ с помощью платья по типу фигуры или стильного костюма.
Давайте разберемся: стилисты выделяют 4 типа фигуры — это песочные часы, трапеция, прямоугольник и треугольник. Рассмотрев все их детально, Вы сможете понять как подобрать одежду по типу фигуры.
ТРАПЕЦИЯ: ЯРКО ВЫРАЖЕНА ТАЛИЯ, БЕДРА ШИРЕ ПЛЕЧ
Фигура-трапеция (груша):
- прямые плечи;
- явное наличие осиной талии;
- округлые ягодицы.
- ИРИНА АЛЛЕГРОВА и БАРБАРА БРЫЛЬСКА представительницы такого типа фигуры.
 Одежда по типу фигуры трапеция — полуприлегающая и табу на обтягивающую.
Одежда по типу фигуры трапеция — полуприлегающая и табу на обтягивающую.
КАК ПОДОБРАТЬ ОДЕЖДУ ПО ФИГУРЕ ТРАПЕЦИЯ:
1) ЮБКА ДЛЯ ТИПА ФИГУРЫ ТРАПЕЦИЯ.
Обладаете красивыми ножками, выбирайте юбки, трапециевидной формы — низ шире, чем верх. Идеальный крой — расклешающиесь книзу юбки по низ колена, сшитые из трапециевидных клиньев или скроенные по косой.
Юбки такого покроя визуально стройнят вашу фигуру и дадут возможность не концентрировать внимание на широких бедрах. Подойдут любые темные оттенки: коричневый, черный. Например, комплект из светлой туники и коричневой юбки одного оттенка будет смотреться просто восхитительно.
Если Вы всеже предпочитаете узкую юбку, знайте, что к лицу она не каждой барышне с таким типом фигуры. Все-таки решили пополнить ей гардероб, тогда параллельно берите тунику, жилет или кардиган и обязательно удлиненный. Хотите акцентировать на своей стройности? Хорошо! Поможет костюм с коротким или полуприлегающим жакетом, он скроет многие изъяны облика.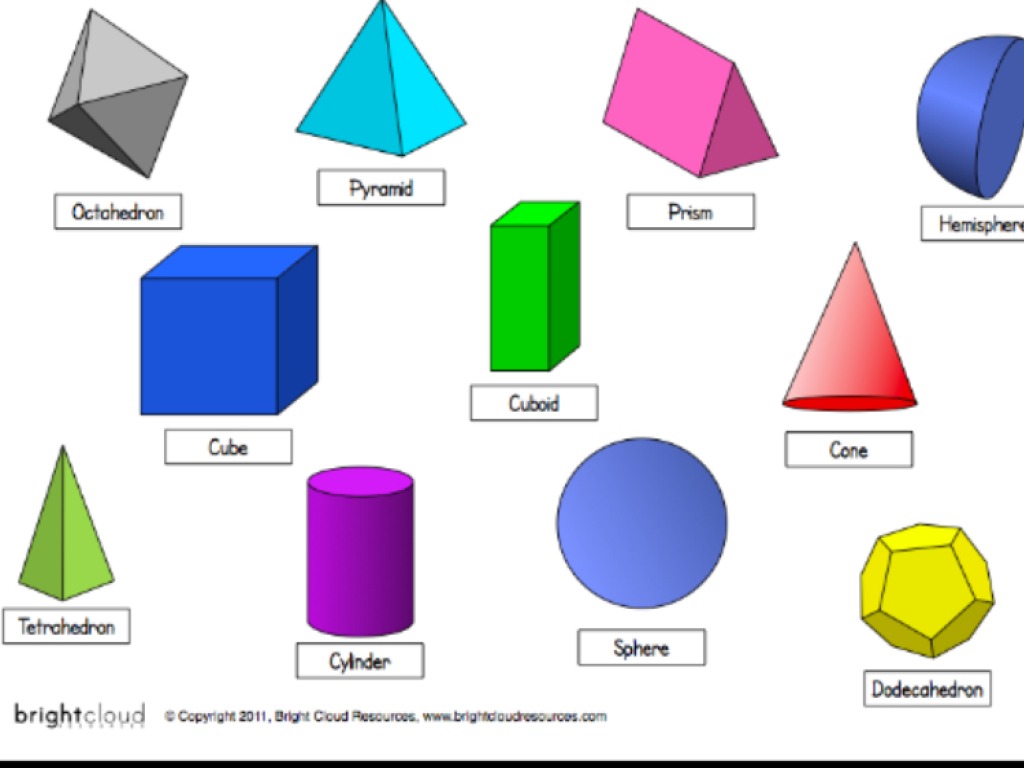
2) БРЮКИ, ДЖИНСЫ ДЛЯ ФИГУРЫ ТРАПЕЦИЯ. ОДЕЖДА ПО ТИПУ ВАШЕЙ ФИГУРЫ
Если Вы считаете, что широкие брюки — это хорошо, мол скрывают широкие бедра. Нет, это не так, это ошибочное мнение. Советуем, выбирать брюки прямые классические, немного зауженные книзу или слегка расширяющиеся. Вас также украсит брючный комплект. Основной ньюанс — пиджак безусловно полуприлегающий длиной ниже линии бедер. Не покупайте прямые блейзеры, они не подчеркивают плавные женственные изгибы тела, а нейтрализуют эффект от них и делают Вас полнее. Подходящие оттенки костюма — темно-синий, серый, черный.
Трапециевидной фигуре подойдут классические прямые джинсы зауженные книзу темно-синего цвета. Так как светлые оттенки выделят круглые бедра, для гармоничного образа этого нужно избегать. Хорошо сядут джинсы с низкой посадкой на талии. Предпочитаете джинсы-стрейч? Тогда носите их с туникой до середины бедра или расширяющимся книзу джемпером, будь они сиреневого или салатового цвета.
3) КОФТОЧКИ, БЛУЗКИ, ТУНИКИ однотонных светлых оттенков — то, что нужно, тем более, если предусмотрен темный низ и желательно пастельного или темного цвета. Платье по типу фигуры покупайте акцентирующее внимание на груди и немного приталенное.
Платье по типу фигуры покупайте акцентирующее внимание на груди и немного приталенное.
Женские платья для фигуры трапеция должны быть в оттенках розового, светло-зеленого, голубого, сиреневого или белого цвета. Красная блузка и черные брючки украсят обладательницу такой фигуры не меньше, чем платье.
4) АКСЕССУАРЫ. Дамам с выдающимися бедрами лучше не носить пояса, в крайнем случае, узкие без утяжки. Обувь подойдет на шпильке или с каблуком средней высоты 3-5 см.
ТРЕУГОЛЬНИК: ПЛЕЧИ ШИРЕ БЕДЕР — ПЕРЕВЕРНУТЫЙ ТРЕУГОЛЬНИК
Фигура — перевернутый треугольник:
- у МОНИКИ БЕЛЛУЧЧИ и ПУГАЧЕВОЙ, и др;
- акцент должен быть сделан на бедра и талию;
- при пополнении гардероба следуйте рекомендациям о 1-м типе фигуры, точно да наоборот;
- цвет одежды должен помочь сконцентрировать внимание на бедрах и талии (белый низ и черный верх).
1) КОФТОЧКИ, БЛУЗКИ, ДЖЕМПЕРА подойдут без горизонтальных полос и крупных узоров. Вертикальные линии кроя одежды. Подойдут с \/-образным выкатом приталенные пиджаки с акцентом ввиде крупных карманов, которые обозначат красивые бедра. Цвета холодных оттенков: синий темный, зеленый или бордово-красный.
Вертикальные линии кроя одежды. Подойдут с \/-образным выкатом приталенные пиджаки с акцентом ввиде крупных карманов, которые обозначат красивые бедра. Цвета холодных оттенков: синий темный, зеленый или бордово-красный.
2) ДЖИНСЫ, БРЮКИ ДЛЯ ФИГУРЫ ПЕРЕВЕРНУТЫЙ ТРЕУГОЛЬНИК.
Барышням с типом фигуры перевернутый треугольник показаны любые фасоны, основное, чтобы штаны выделяли достоинства, а не наоборот. В нашей ситуации довольно гармонично будут выглядеть светлые голубые брюки или деним. Вот например, замечательно и выгодно смотрятся обтягивающие блузки или рубашки совместно с такими же светлыми голубыми джинсами. Отлично украсит девушку с типом фигуры треугольник костюм брючный в вертикальную полоску светлого коричневого тона, а полосы более темного цвета, чем сама двойка или тройка.
3) ДЛИНА ЮБКИ — по Вашему желанию! Она может зависеть только от одного — желаете Вы показать стройность своих ног либо же нет. Цвета ткани светлые, хотите в клетку или в косую линию, хороши также узоры, так как акцентируют внимание на себе.
ПРЯМОУГОЛЬНИК: БЕДРА И ПЛЕЧИ ПРОПОРЦИОНАЛЬНЫ, ТАЛИЯ ВЫРАЖЕНА НЕЧЕТКО
Фигура — колонна:
- представительницы ПАМЕЛА АНДЕРСОН и ЕВА ПОЛЬНА, и др;
- основное — акцент на талию для стройности;
- топы приталенные и чуть ниже талии;
- табу на широкую одежду, так как этот вариант, прячет одни недостатки, но добавляет других.
1) БРЮКИ И ЮБКИ — без пояса! По цвету низ и верх — тон в тон. Например, темная юбка подойдет под темную блузку, одно но — с ярким цветочным принтом. Вы можете носить брюки-капри, опять же при 1-м условии, если ваши ножки стройны и длинны.
Прямоугольный тип фигуры для барышень сулит платья на бретельках и с прямым вырезом.
2) БЛЕЙЗЕРЫ лишь прямого кроя. Кофточки и блузки синего, красного, зеленого или кремового цвета украсят с небольшими рукавами «реглант».
3) Любите украшать талию АКСЕССУАРАМИ? Отныне табу на пояса и ремни. Они лишь подчеркнут недостатки. Обувь советуем на небольшом каблуке или платформе.
ПЕСОЧНЫЕ ЧАСЫ: БЕДРА И ПЛЕЧИ ОДИНАКОВОЙ ПРОПОРЦИИ, ТАЛИЯ ЯРКО ВЫРАЖЕНА
Фигура — X-образная:
- ЛЮБОВЬ ПОЛИЩУК и НАТАЛЬЯ ОРЕЙРО;
- основное — приталенные блузки, пиджаки, топы, платья, а не безразмерные;
- идет практически все, если это выглядит элегантно и красиво.
1) ДЖИНСЫ И БРЮКИ желательно с низкой посадкой. Широкие штаны не покупайте, хотя, бывают исключения.
Допустим, светлая блузка под корсетом + темные широкие брючки — довольно стильно и оригинально выглядит; или облегающая кофточка глубокого красного оттенка под насыщенно-синий деним.
2) Различные АКСЕССУАРЫ и обувь на высоком каблуке, и все, что нравится. Подчеркнем, что перебор в деталях не пойдет ни кому из фигуристых женщин.
Дорогие женщины, эти рекомендации призваны немного облегчить Вам жизнь и помочь купить новую подходящую одежду по типу фигуры. А самое главное ощутить себя уверенными и желанными!
НЕОБХОДИМЫЕ ВЕЩИ В ГАРДЕРОБЕ СОВРЕМЕННОЙ ЖЕНЩИНЫ
- Брюки — 2 пары, желательно темных тонов: — из плотной ткани для повседневной носки; — из тонкой ткани свободного фасона, отличного качества и обязательно по фигуре.

- Джинсы — 2 пары — универсальная вещь, так как легко дополняют любую одежду. Лучше разной длины: — под обувь на каблуке; — под спортивную обувь.
- Юбки — две: трапеция, диагонального покроя полусолнце из драпирующейся материи; плотная темная прямая, чуть расклешенная или зауженная.
- Блузка светлая с застежкой спереди.
- N-ое количество футболок.
- Свитера — 3 тонких на пуговичках: яркий, нейтральный и темный.
- Жакеты — 2: 1-й = крой спортивный для отдыха и работы, 2-й темный дополняющий черную юбку или брюки.
- Платье или двойка — юбка и блузка, сочетающаясь в платье.
Какие геометрические фигуры. Геометрические фигуры для детей
Геометрия – точная математическая наука, которая занимается изучением пространственных и других подобных отношений и форм. Но ее часто называют «сухой», поскольку она не способна описать форму многих природных объектов, ведь облака – это не сферы, горы – не конусы, а молнии распространяются не по прямым линиям. Многие объекты в природе отличаются сложностью форм в сравнении со стандартной геометрией.
Многие объекты в природе отличаются сложностью форм в сравнении со стандартной геометрией.
Тем не менее, существует ряд удивительных фигур, которые обычно не изучаются на школьных уроках геометрии, но именно они окружают человека в реальном мире: в природе и архитектуре, головоломках, компьютерных играх и т. д.
Главное свойство этой сложной геометрической фигуры – самоподобие, то есть она состоит из нескольких частей, каждая из которых подобна целому объекту. Именно это свойство отличает фракталы от объектов классической (или, как говорят, евклидовой) геометрии.
При этом сам термин «фрактал» не является математическим и не имеет однозначного определения, поэтому может применяться к объектам, которые являются самоподобными или приближенно самоподобными. Его придумал в 1975 г. Бенуа Мандельброт, позаимствовав латинское слово «fractus» (ломанный, дробленный).
Фрактальные формы как нельзя лучше подходят для описания реального мира и часто встречаются среди природных объектов: снежинок, листьев растений, системы кровеносных сосудов человека и животных.
Это одна из самых необыкновенных трехмерных фигур в геометрии, которую легко сделать в домашних условиях. Для этого достаточно взять бумажную полоску, ширина которой в 5-6 раз меньше ее длины, и, перекрутив один из концов на 180°, склеить их между собой.
Если все сделано правильно, то можно проверить самостоятельно ее удивительные свойства:
- Наличие только одной стороны (без разделения на внутреннюю и внешнюю). Это легко проверить, если попробовать закрасить карандашом одну из ее сторон. Независимо от того, в каком месте и направлении будет начато закрашивание, в результате вся лента будет закрашена одним цветом.
- Непрерывность: если вести ручкой линию вдоль всей поверхности, ее конец соединится с начальной точкой без пересечения границ поверхности.
- Двухмерность (связность): при разрезании ленты Мебиуса вдоль она остается цельной, просто получаются новые фигуры (к примеру, при разрезании надвое получится одно кольцо большего размера).
- Отсутствие ориентированности.
 Путешествие по такой ленте Мебиуса всегда будет бесконечным, оно приведет к начальной точке пути, только в зеркальном отображении.
Путешествие по такой ленте Мебиуса всегда будет бесконечным, оно приведет к начальной точке пути, только в зеркальном отображении.
Лента Мебиуса широко используется в промышленности и науке (в ленточных конвейерах, матричных принтерах, механизмах для заточки и пр.). Кроме этого существует научная гипотеза, по которой сама Вселенная также представляет собой ленту Мебиуса невероятных размеров.
Полимино
Это плоские геометрические фигуры, которые образуются за счет соединения нескольких квадратов равных размеров по их сторонам.
Названия полимино зависят от количества квадратов, из которых они сформированы:
- мономино – 1;
- домино – 2;
- тримино – 3;
- тетрамино – 4 и т. д.
При этом для каждой разновидности существует разное количество типов фигур: у домино 1 тип, у тримино – 3 типа, у гексамино (из 6 квадратов) – 35 типов. Число различный вариаций зависит от количества используемых квадратов, но при этом еще никому из ученых не удалось найти удивительную формулу, которая будет выражать эту зависимость. Из деталей полимино можно выкладывать как геометрические фигуры, так и изображения людей, животных, предметов. Несмотря на то, что это будут схематичные силуэты, основные признаки и формы предметов делают их вполне узнаваемыми.
Из деталей полимино можно выкладывать как геометрические фигуры, так и изображения людей, животных, предметов. Несмотря на то, что это будут схематичные силуэты, основные признаки и формы предметов делают их вполне узнаваемыми.
Полиамонд
Наряду с полимино, существует еще одна удивительная геометрическая фигура, используемая для составления других фигур – полиамонд. Он представляет собой многоугольник, сформированный из нескольких равносторонних треугольников равного размера.
Название придумал математик Т. О’Бейрн на основании одного из названий ромба в английском языке – диамонд, который можно составить из 2-х равносторонних треугольников. По аналогии, фигуру из 3-х равносторонних треугольников О’Бейрн назвал триамондом, из 4-х – тетриамондом и т. д.
Главным вопросом их существования остается вопрос о возможном количестве полиамондов, которые можно составить из определенного количества треугольников. Применение полиамондов в реальной жизни также аналогично использованию полимино.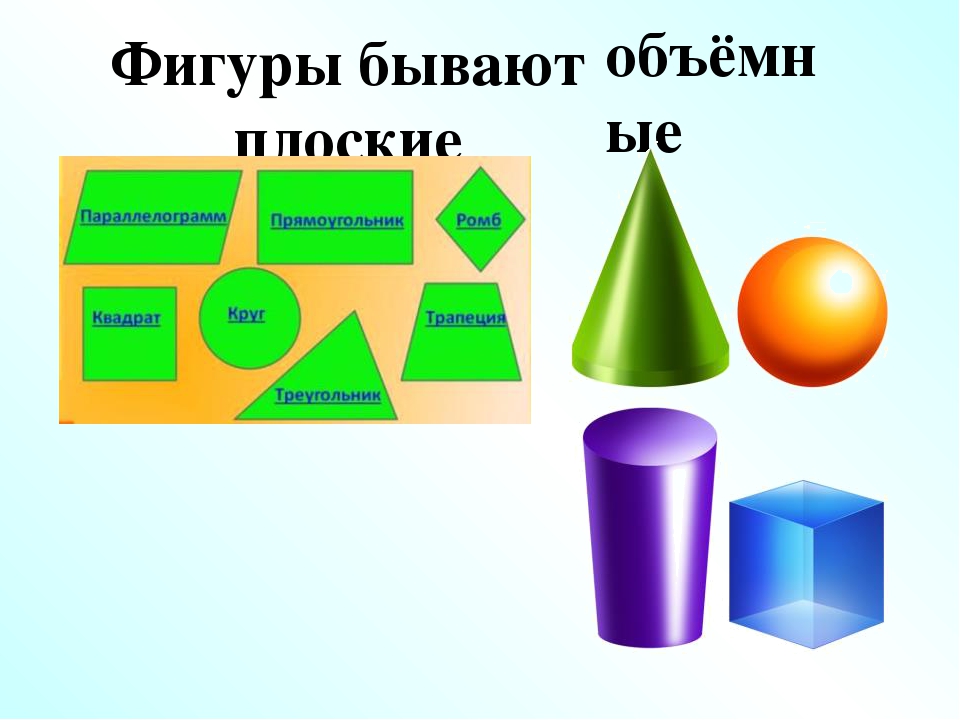 Это могут быть разного рода головоломки и логические задачи.
Это могут быть разного рода головоломки и логические задачи.
Треугольник Рело
Как ни удивительно звучит, но с помощью дрели можно просверлить квадратное отверстие, а помогает в этом треугольник Рело. Он представляет собой область, образованную посредством пересечения 3 равных окружностей, центры которых являются вершинами правильного треугольника, а радиусы равны его стороне.
Сам треугольник Рело назван по фамилии немецкого ученого-инженера, который первым наиболее детально исследовал его особенности и использовал для своих механизмов на рубеже XIX-XX в. в., хотя его удивительные свойства были известны еще Леонардо да Винчи. Кто бы ни был его первооткрывателем, в современном мире эта фигура нашла широкое применение в виде:
- сверла Уаттса, которое позволяет сверлить отверстия практически идеальной квадратной формы, только с чуть закругленными краями;
- медиатора, необходимого для игры на музыкальных щипковых инструментах;
- кулачковых механизмов, используемых для создания зигзагообразных швов в швейных машинах, а также немецких часах;
- стрельчатых арок, характерных для готического стиля в архитектуре.

Отдельного внимания заслуживают так называемые невозможные фигуры – удивительные оптические иллюзии, которые на первый взгляд кажутся проекцией трехмерного объекта, но при ближайшем рассмотрении становятся заметны необычные соединения элементов. Наиболее популярными из их числа являются:
Трибар, созданный отцом и сыном Лайонелом и Роджером Пенроузами, который представляет собой изображение равностороннего треугольника, но имеет странные закономерности. Стороны, образующие верхнюю часть треугольника кажутся перпендикулярными, но правая и левая грани в нижней части также кажутся перпендикулярными. Если рассматривать каждую часть этого треугольника по отдельности, еще можно признать их существование, но в действительности такая фигура существовать не может, поскольку при ее создании были неправильно соединены правильные элементы.
Бесконечная лестница, авторство которой также принадлежит отцу и сыну Пенроузам, поэтому ее часто называют по их имени – «лестницей Пенроуза», а также «Вечной лестницей».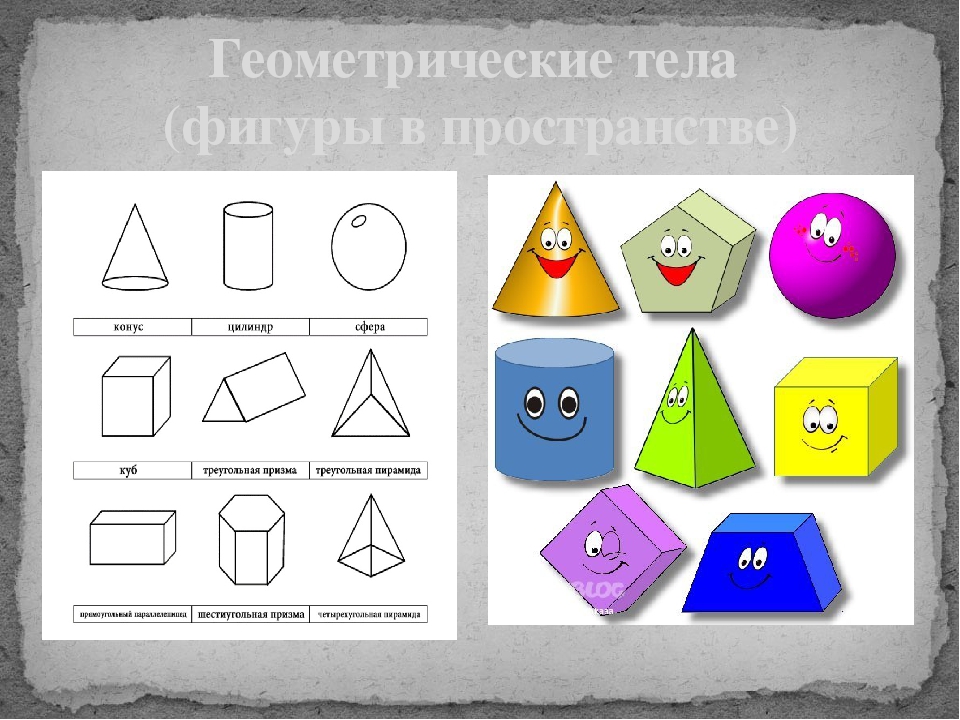 На первый взгляд, она выглядит как обычная, ведущая вверх или вниз лестница, но при этом человек, шагающий по ней будет непрерывно подниматься (против часовой стрелки) или опускаться (по часовой стрелке). Если визуально путешествовать по такой лестнице, то по окончании «путешествия» взгляд останавливается в точке начала пути. Если бы такая лестница существовала в действительности, по ней пришлось бы подниматься и спускаться бесконечное число раз, что можно сравнить с бесконечным сизифовым трудом.
На первый взгляд, она выглядит как обычная, ведущая вверх или вниз лестница, но при этом человек, шагающий по ней будет непрерывно подниматься (против часовой стрелки) или опускаться (по часовой стрелке). Если визуально путешествовать по такой лестнице, то по окончании «путешествия» взгляд останавливается в точке начала пути. Если бы такая лестница существовала в действительности, по ней пришлось бы подниматься и спускаться бесконечное число раз, что можно сравнить с бесконечным сизифовым трудом.
Невозможный трезубец – удивительный объект, глядя на который невозможно определить, где начинается средний зубец. Он также основан на принципе неправильных соединений, которые могут существовать только в двухмерном, но не трехмерном пространстве. Рассматривая части трезубца по отдельности, с одной стороны видны 3 круглых зуба, с другой стороны – 2 прямоугольных.
Таким образом, части фигуры вступают в своеобразный конфликт: во-первых, происходит смена переднего и заднего плана, во-вторых круглые зубцы в нижней части трансформируются в плоские в верхней.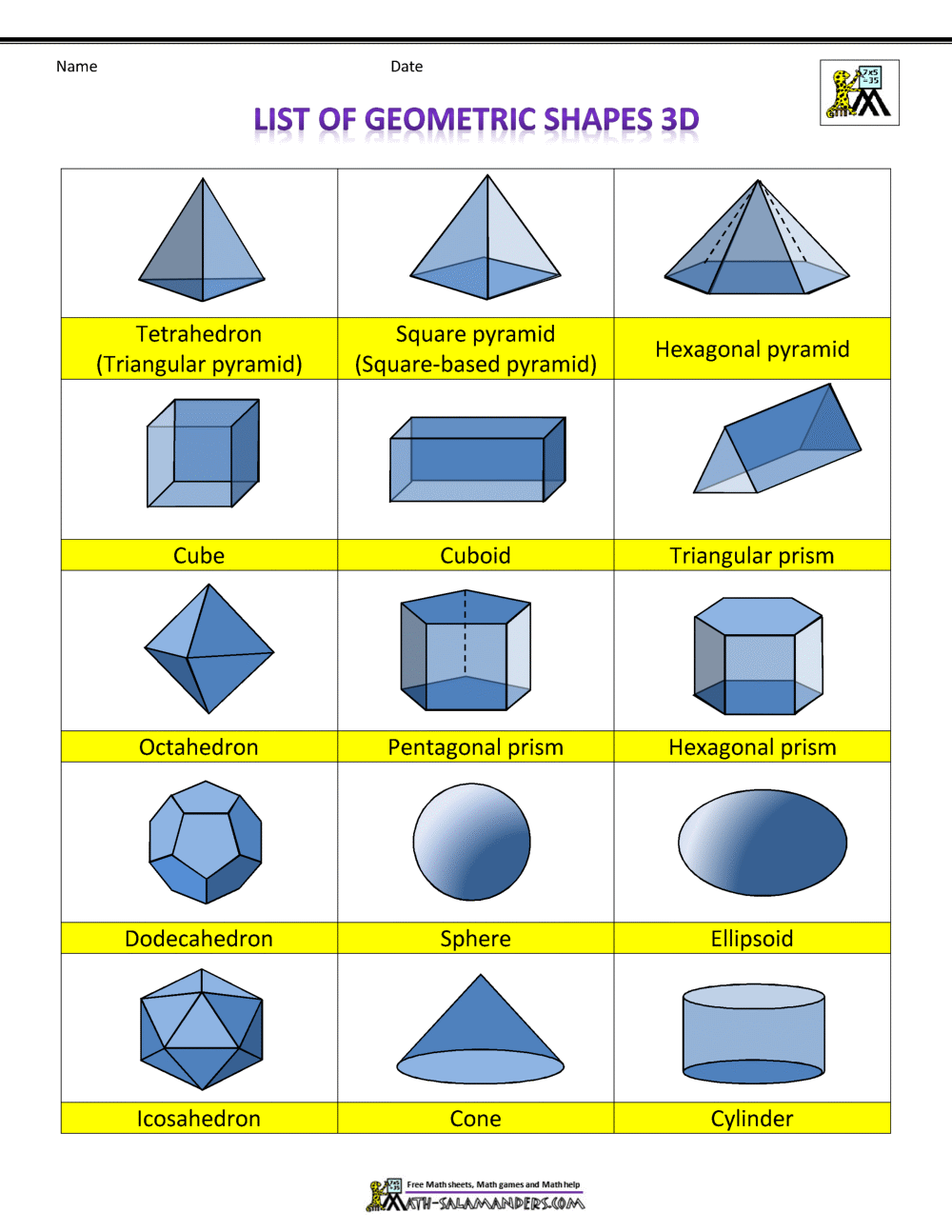
Тема урока
Геометрические фигуры
Что такое геометрическая фигура
Геометрические фигуры – это совокупность множества точек, линий, поверхностей или тел, которые расположены на поверхности, плоскости или пространстве и формирует конечное количество линий.
Термин «фигура» в какой-то степени формально применяется к множеству точек, но как правило фигурой принято называть такие множества, которые расположенные на плоскости и ограничиваются конечным числом линий.
Точка и прямая — это основные геометрические фигуры, расположенные на плоскости.
К самым простым геометрическим фигурам на плоскости принадлежат — отрезок, луч и ломаная линия.
Что такое геометрия
Геометрия – это такая математическая наука, которая занимается изучением свойств геометрических фигур. Если дословно перевести на русский язык термин «геометрия», то он обозначает «землемерие», так как в стародавние времена основной задачей геометрии, как науки, стало измерение расстояний и площадей на поверхности земли.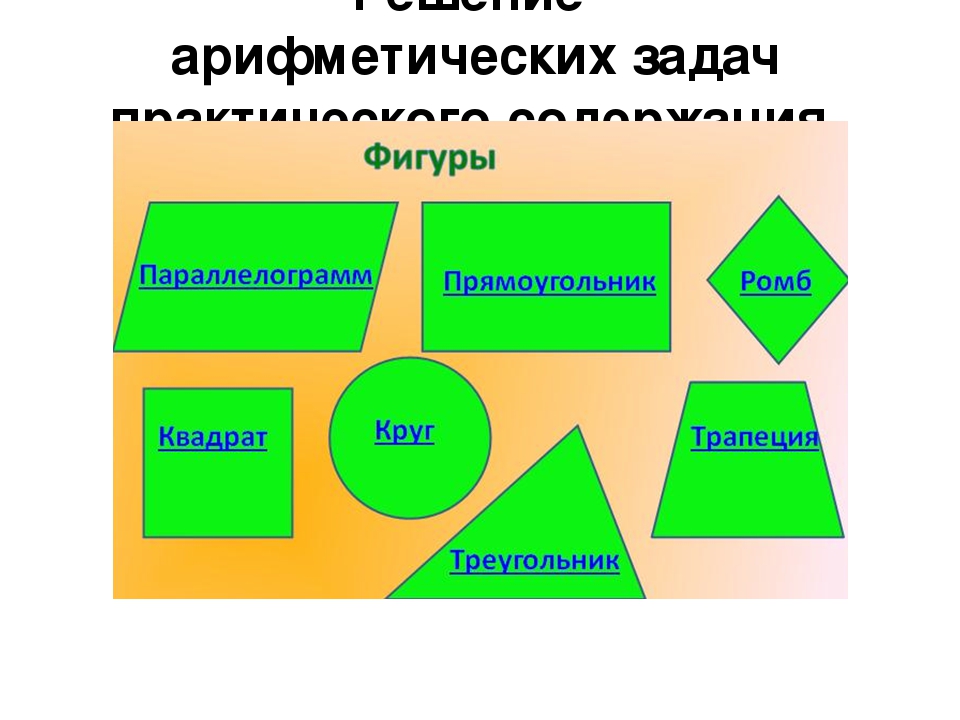
Практическое применение геометрии бесценно во все времена и независимо от профессии. Без знаний геометрии не может обойтись ни рабочий, ни инженер, ни архитектор и даже художник.
В геометрии есть такой раздел, который занимается изучением различных фигур на плоскости и называется планиметрия.
Вам уже известно, что фигурой называют произвольное множество точек, находящиеся на плоскости.
К геометрическим фигурам принадлежат: точка, прямая, отрезок, луч, треугольник, квадрат, круг и другие фигуры, которые изучает планиметрия.
Точка
Из выше изученного материала вам уже известно, что точка относится к главным геометрическим фигурам. И хотя это самая малая геометрическая фигура, но она необходима для построения других фигур на плоскости, чертеже или изображении и является основой для всех остальных построений. Ведь построение более сложноватых геометрических фигур складывается из множества точек, характерных для данной фигуры.
В геометрии точки обозначают прописными буквами латинского алфавита, например, такими, как: А, В, С, D ….
А теперь подведем итог, и так, с математической точки зрения, точка является таким абстрактным объектом в пространстве, который не имеет объема, площади, длины и других характеристик, но остается одним из фундаментальных понятий в математике. Точка – это такой нульмерный объект, которые не имеет определения. По определению Евклида, точкой называют то, что невозможно определить.
Прямая
Как и точка, прямая относится к фигурам на плоскости, которая не имеет определения, так как состоит из бесконечного множества точек, находящихся на одной линии, которая не имеет ни начала ни конца. Можно утверждать, что прямая линия бесконечна и не имеет предела.
Если же прямая начинается и заканчивается точкой, то она уже не является прямой и называется отрезком.
Но иногда прямая, с одной стороны имеет точку, а с другой нет. В таком случае прямая превращается в луч.
Если же взять прямую и на ее средине поставить точку, то она разобьет прямую на два противоположно направленных луча. Данные лучи являются дополнительными.
Данные лучи являются дополнительными.
Если же перед вами несколько отрезков, соединенных между собой так, что конец первого отрезка становиться началом второго, а конец второго отрезка — началом третьего и т. д., и эти отрезки находятся не на одной прямой и при соединении имеют общую точку, то такая цепочка является ломаной линией.
Задание
Какая ломаная линия называется незамкнутой?
Как обозначается прямая?
Как называется ломаная линия, у которой четыре замкнутых звена?
Какое название имеет ломаная линия с тремя замкнутыми звеньями?
Когда конец последнего отрезка ломаной совпадает с началом 1-го отрезка, то такую ломаную линию называют замкнутой. Примером замкнутой ломаной является любой многоугольник.
Плоскость
Как точка и прямая, так и плоскость является первичным понятием, не имеет определения и у нее нельзя увидеть ни начала, ни конца. Поэтому, при рассмотрении плоскости, мы рассматриваем только ту ее часть, которая ограничивается замкнутой ломаной линией. Таким образом, плоскостью можно считать любую гладкую поверхность. Этой поверхностью может быть лист бумаги или стола.
Таким образом, плоскостью можно считать любую гладкую поверхность. Этой поверхностью может быть лист бумаги или стола.
Угол
Фигура, которая имеет два луча и вершину, называется углом. Место соединения лучей, является вершиной этого угла, а его сторонами считаются лучи, которые этот угол образуют.
Задание:
1. Как в тексте обозначают угол?
2. Какими единицами можно измерить угол?
3. Какие бывают углы?
Параллелограмм
Параллелограмм — это четырехугольник, противолежащие стороны которого попарно параллельны.
Прямоугольник, квадрат и ромб являются частными случаями параллелограмма.
Параллелограмм, имеющий прямые углы равные 90 градусам, является прямоугольником.
Квадрат — это тот же параллелограмм, у него и углы и стороны равны.
Что до определения ромба, то это такая геометрическая фигура, все стороны которого равны.
Кроме того, следует знать, что любой квадрат является ромбом, но не каждый ромб может быть квадратом.
Трапеция
При рассмотрении такой геометрической фигуры, как трапеция, можно сказать, что в частности она, как и четырехугольник имеет одну пару параллельных противолежащих сторон и является криволинейной.
Окружность и круг
Окружность — геометрическое место точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое её радиусом.
Треугольник
Также к простым геометрическим фигурам принадлежит и уже изучаемый вами треугольник. Это один из видов многоугольников, у которого часть плоскости ограничена тремя точками и тремя отрезками, которые соединяют эти точки попарно. Любой треугольник имеет три вершины и три стороны.
Задание: Какой треугольник называют вырожденным?
Многоугольник
К многоугольникам относятся геометрические фигуры разных форм, у которых замкнутая ломаная линия.
В многоугольнике все точки, которые соединяют отрезки, являются его вершинами. А отрезки, из которых состоит многоугольник, являются его сторонами.
А отрезки, из которых состоит многоугольник, являются его сторонами.
А известно ли вам, что возникновение геометрии уходит в глубину веков и связано с развитием различных ремесел, культуры, искусства и наблюдением за окружающим миром. Да и название геометрических фигур является тому подтверждением, так как их термины, возникли не просто так, а благодаря своей схожести и подобию.
Ведь термин «трапеция» в переводе с древнегреческого языка от слова «трапезион» обозначает столик, трапеза и другие производные слова.
«Конус» произошел от греческого слова «конос», что в переводе звучит, как сосновая шишка.
«Линия» имеет латинские корни и происходит от слова «линум», в переводе это звучит, как льняная нить.
А знаете ли вы, что если взять геометрические фигуры с одинаковым периметром, то среди них обладателем самой большой площади оказался круг.
Геометрические фигуры — это замкнутые множества точек на плоскости или в пространстве, которые ограничены конечным числом линий. Они могут быть линейными (1D), плоскими (2D) или пространственными (3D).
Они могут быть линейными (1D), плоскими (2D) или пространственными (3D).
Любое тело, имеющее форму, представляет собой совокупность геометрических фигур.
Любую фигуру можно описать математической формулой различной степени сложности. Начиная от простого математического выражения до суммы рядов математических выражений.
Основными математическими параметрами геометрических фигур являются радиусы, длины сторон или граней и углы между ними.
Ниже представлены основные геометрические фигуры, наиболее часто используемые в прикладных расчетах, формулы и ссылки на расчетные программы.
Линейные геометрические фигуры
1. ТочкаТочка — это базовый объект измерения. Основной и единственной математической характеристикой точки является её координата.
2. Линия
Линия — это тонкий пространственный объект имеющий конечную длину и представляющий собой цепь связанных друг с другом точек. Основной математической характеристикой линии является длина.
Луч — это тонкий пространственный объект имеющий бесконечную длину и представляющий собой цепь связанных друг с другом точек. Основными математическими характеристиками луча являются координата его начала и направление.
Основными математическими характеристиками луча являются координата его начала и направление.
Плоские геометрические фигуры
1. КругКруг — это геометрическое место точек на плоскости, расстояние от которых до его центра, не превышает заданного числа, называемого радиусом этого круга. Основной математической характеристикой круга является радиус.
2. Квадрат
Квадрат — это четырёхугольник, у которого все углы и все стороны равны. Основной математической характеристикой квадрата является длина его стороны.
3. Прямоугольник
Прямоугольник — это четырехугольник, у которого все углы равны 90 градусам (прямые). Основными математичскими характеристиками прямоугольника являются длины его сторон.
4. Треугольник
Треугольник — это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки (вершины треугольника), не лежащие на одной прямой. Основными математическими характеристиками треугольника являются длины сторон и высота.
5. Трапеция
Трапеция — это четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Основными математическими характеристиками трапеции являются длины сторон и высота.
6. Параллелограмм
Параллелограмм — это четырёхугольник, у которого противоположные стороны параллельны. Основными математическими характеристиками параллелограмма являются длины его сторон и высота.
Ромб — это четырехугольник, у которого все стороны, а углы его вершин не равны 90 градусам. Основными математическими характеристиками ромба являются длина его стороны и высота.
8. Эллипс
Эллипс — это замкнутая кривая на плоскости, которая может быть представлена как ортогональная проекция сечения окружности цилиндра на плоскость. Основными математическими характеристиками окружности являются длина его полуосей.
Объемные геометрические фигуры
1. ШарШар — это геометрическое тело, представляющее собой совокупность всех точек пространства, находящихся от его центра на заданном расстоянии. Основной математической характеристикой шара является его радиус.
Основной математической характеристикой шара является его радиус.
Сфера — это оболочка геометрического тела, представляющее собой совокупность всех точек пространства, находящихся от его центра на заданном расстоянии. Основной математической характеристикой сферы является её радиус.
Куб — это геометрическое тело, представляющее собой правильный многогранник, каждая грань которого представляет собой квадрат. Основной математической характеристикой куба является длина его ребра.
4. Параллелепипед
Параллелепипед — это геометрическое тело, представляющее собой многогранник, у которого шесть граней и каждая из них прямоугольник. Основными математическими характеристиками параллелепипеда являются длины его ребер.
5. Призма
Призма — это многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани параллелограммами, имеющими общие стороны с этими многоугольниками. Основными математическими характеристиками призмы являются площадь основания и высота.
Конус — это геометрическая фигура, полученная объединением всех лучей, исходящих из одной вершины конуса и проходящих через плоскую поверхность. Основными математическими характеристиками конуса являются радиус основания и высота.
7. Пирамида
Пирамида — это многогранник, основанием которого является произвольный многоугольник, а боковые грани являются треугольниками, имеющие общую вершину. Основными математическими характеристиками пирамиды являются площадь основания и высота.
8. Цилиндр
Цилиндр — это геометрическая фигура, ограниченная цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её. Основными математическими характеристиками цилиндра являются радиус основания и высота.
Быстро выполнить эти простейшие математические операции можно с помощью наших онлайн программ. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлены все геометрические фигуры, которые наиболее часто встречаются в геометрии для представления объекта или его части на плоскости или в пространстве.
Существует бесконечное множество форм. Формой называют внешнее очертание предмета.
Изучение форм можно начинать с самого раннего детства, обращая внимание своего ребенка на окружающий нас мир, который состоит из фигур (тарелка – круглая, телевизор – прямоугольный).
Уже с двух лет малыш должен знать три простые фигуры – круг, квадрат, треугольник. Сначала он их должен просто показывать, когда вы это просите. А в три года уже называть их самостоятельно и отличать круг от овала, квадрат от прямоугольника.
Чем больше упражнений на закрепление форм будет выполнено ребенком, тем больше новых фигур он запомнит.
Будущий первоклашка должен знать все простые геометрические фигуры и уметь составлять из них аппликации.
Что мы называем геометрической фигурой?
Геометрическая фигура — это эталон, с помощью которого можно определить форму предмета или его частей.
Фигуры разделяют на две группы: плоские фигуры, объемные фигуры.
Плоскими фигурами мы назовем те фигуры, которые расположены в одной плоскости.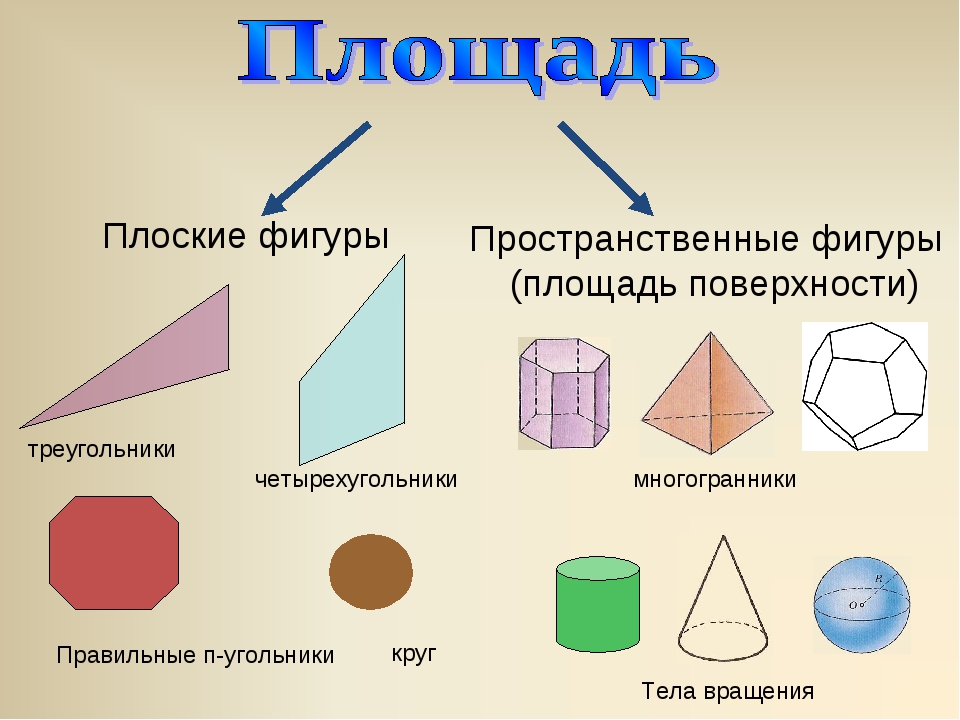 К ним относятся круг, овал, треугольник, четырёхугольник (прямоугольник, квадрат, трапеция, ромб, параллелограмм) и всевозможные многоугольники.
К ним относятся круг, овал, треугольник, четырёхугольник (прямоугольник, квадрат, трапеция, ромб, параллелограмм) и всевозможные многоугольники.
К объемным фигурам относят: сфера, куб, цилиндр, конус, пирамида. Это те фигуры, которые имеют высоту, ширину и глубину.
Следуйте двум простым советам при объяснении геометрических фигур:
- Терпение. То, что нам, взрослым, кажется простым и логичным ребенку покажется просто непонятным.
- Попробуйте рисовать фигуры вместе с ребенком.
- Игра. Начинайте изучать фигуры в игровой форме. Хорошие упражнения для закрепления и изучения плоских форм – аппликации из геометрических фигур. Для объемных – можно использовать готовые покупные игры, а также выбирать аппликации, где можно вырезать и склеивать объемную форму.
Геометрические фигуры представляют собой комплекс точек, линий, тел или поверхностей. Эти элементы могут располагаться как на плоскости, так и в пространстве, формируя конечное количество прямых.
Термин «фигура» подразумевает под собой несколько множеств точек. Они должны располагаться на одной или нескольких плоскостях и одновременно ограничиваться конкретным числом оконченных линий.
Основными геометрическими фигурами считаются точка и прямая. Они располагаются на плоскости. Кроме них, среди простых фигур выделяют луч, ломаную линию и отрезок.
Точка
Это одна из главных фигур геометрии. Она очень маленькая, но ее всегда используют для построения различных форм на плоскости. Точка — это основная фигура для абсолютно всех построений, даже самой высокой сложности. В геометрии ее принято обозначать буквой латинской алфавита, к примеру, A, B, K, L.
С точки зрения математики точка — это абстрактный пространственный объект, не обладающий такими характеристиками, как площадь, объем, но при этом остающийся фундаментальным понятием в геометрии. Этот нульмерный объект просто не имеет определения.
Прямая
Это фигура полностью размещается в одной плоскости. У прямой нет конкретного математического определения, так как она состоит из огромного количества точек, располагающихся на одной бесконечной линии, у которой нет предела и границ.
У прямой нет конкретного математического определения, так как она состоит из огромного количества точек, располагающихся на одной бесконечной линии, у которой нет предела и границ.
Существует еще и отрезок. Это тоже прямая, но она начинается и заканчивается с точки, а значит, имеет геометрические ограничения.
Также линия может превратиться в направленный луч. Такое происходит, когда прямая начинается с точки, но четкого окончания не имеет. Если же поставить точку посредине линии, то она разобьется на два луча (дополнительных), причем противоположно направленных друг к другу.
Несколько отрезков, которые последовательно соединяются друг с другом концами в общей точке и располагаются не на одной прямой, принято называть ломаной линией.
Угол
Геометрические фигуры, названия которых мы рассмотрели выше, считают ключевыми элементами, использующимися при построении более сложных моделей.
Угол — это конструкция, состоящая из вершины и двух лучей, которые выходят из нее. То есть стороны этой фигуры соединяются в одной точке.
То есть стороны этой фигуры соединяются в одной точке.
Плоскость
Рассмотрим еще одно первичное понятие. Плоскость — это фигура, у которой нет ни конца, ни начала, равно как и прямой, и точки. Во время рассмотрения этого геометрического элемента во внимание берется лишь его часть, ограниченная контурами ломаной замкнутой линии.
Любую гладкую ограниченную поверхность можно считать плоскостью. Это может быть гладильная доска, лист бумаги или даже дверь.
Четырехугольники
Параллелограмм — это геометрическая фигура, противоположные стороны которой параллельны друг другу попарно. Среди частных видов этой конструкции выделяют ромб, прямоугольник и квадрат.
Прямоугольник — это параллелограмм, у которого все стороны соприкасаются под прямым углом.
Квадрат — это четырехугольник с равными сторонами и углами.
Ромб — это фигура, у которой все грани равны. При этом углы могут быть совершенно разными, но попарно. Каждый квадрат считается ромбом. Но в противоположном направлении это правило действует не всегда. Далеко не каждый ромб является квадратом.
Но в противоположном направлении это правило действует не всегда. Далеко не каждый ромб является квадратом.
Трапеция
Геометрические фигуры бывают совершенно разными и причудливыми. Каждая из них имеет своеобразную форму и свойства.
Трапеция — это фигура, которая чем-то схожа с четырехугольником. Она имеет две параллельные противоположные стороны и при этом считается криволинейной.
Круг
Эта геометрическая фигура подразумевает расположение на одной плоскости точек, равноудаленных от ее центра. При этом заданный ненулевой отрезок принято называть радиусом.
Треугольник
Это простая геометрическая фигура, которая очень часто встречается и изучается.
Треугольник считается подвидом многоугольника, расположенным на одной плоскости и ограниченным тремя гранями и тремя точками соприкосновения. Эти элементы попарно соединены между собой.
Многоугольник
Вершинами многоугольников называют точки, соединяющие отрезки. А последние, в свою очередь, принято считать сторонами.
Объемные геометрические фигуры
- призма;
- сфера;
- конус;
- цилиндр;
- пирамида;
Эти тела имеют нечто общее. Все они ограничиваются замкнутой поверхностью, внутри которой находится множество точек.
Объемные тела изучают не только в геометрии, но и в кристаллографии.
Любопытные факты
Наверняка вам будет интересно ознакомиться с информацией, предоставленной ниже.
- Геометрия сформировалась как наука еще в давние века. Это явление принято связывать с развитием искусства и разнообразных ремесел. А названия геометрических фигур свидетельствуют об использовании принципов определения подобия и схожести.
- В переводе с древнегреческого термин «трапеция» обозначает столик для трапезы.
- Если вы возьмете различные фигуры, периметр которых будет одинаковым, то наибольшая площадь гарантированно будет у круга.
- В переводе с греческого языка термин «конус» обозначает сосновую шишку.
- Существует известная картина Каземира Малевича, которая начиная с прошлого века притягивает к себе взгляды многих живописцев.
 Работа «Черный квадрат» всегда была мистической и загадочной. Геометрическая фигура на белом полотне восхищает и поражает одновременно.
Работа «Черный квадрат» всегда была мистической и загадочной. Геометрическая фигура на белом полотне восхищает и поражает одновременно.
Существует большое количество геометрических фигур. Все они отличаются параметрами, а порой даже удивляют формами.
Фигура речи – Примеры и определение фигуры речи
Определение фигуры речи
Фигура речи – это слово или фраза, которые используются небуквальным образом для создания эффекта. Этот эффект может быть риторическим, как при преднамеренном расположении слов для достижения чего-то поэтического, или образным, как при использовании языка, чтобы предложить визуальную картину или сделать идею более яркой. В целом, фигуры речи функционируют как литературные средства из-за их выразительного использования языка.Слова используются иначе, чем их буквальное значение или типичный способ применения.
Например, Маргарет Этвуд использует обороты речи в своем стихотворении «Ты вписываешься в меня» как средство достижения поэтического смысла и создания яркой картины для читателя.
ты вписываешься в меня
как крючок в глаз
рыболовный крючок
открытый глаз крючок и застежка на глаз, возможно, для одежды.Это пример риторического эффекта, поскольку формулировка тщательно передает идею двух вещей, предназначенных для соединения друг с другом. Во вторых двух строках формулировка уточняется добавлением «рыба» к «крючку» и «открытого» к «глазу», что вызывает неприятный и даже жестокий образ. Описания поэтом крючков и глаз в стихотворении не означают буквально. И все же использование образного языка позволяет поэту выразить два очень разных смысла и образа, которые усиливают интерпретацию стихотворения за счет контраста.
Типы фигур речи
Термин фигура речи охватывает широкий спектр литературных приемов, приемов и других форм образного языка, некоторые из которых включают:
Общие примеры фигур речи, используемых в разговоре
Многие люди используют обороты речи в разговоре, чтобы прояснить или подчеркнуть то, что они имеют в виду.
Вот несколько распространенных примеров разговорных фигур речи:
Гипербола
Гипербола — это фигура речи, в которой используется крайнее преувеличение, чтобы подчеркнуть определенное качество или особенность.
- У меня миллион дел.
- Этот чемодан весит тонну.
- Эта комната представляет собой холодильник.
- Я умру, если он не пригласит меня на свидание.
- Я слишком беден, чтобы обращать внимание.
Преуменьшение
Преуменьшение — это фигура речи, которая вызывает меньше эмоций, чем можно было бы ожидать в ответ на что-либо. Это преуменьшение реакции является неожиданностью для читателя и обычно вызывает иронию.
- Я слышал, что у нее рак, но это не имеет большого значения.
- Джо получил работу своей мечты, так что это не так уж и плохо.
- Сью выиграла в лотерею, так что она немного взволнована.
- Этот заброшенный дом просто нуждается в покраске.
- Ураган принес с собой пару ливней.
Парадокс
Парадокс — это фигура речи, которая кажется противоречивой, но на самом деле раскрывает нечто истинное.
- Вы должны потратить деньги, чтобы сохранить его.
- Я понял, что ничего не знаю.
- Чтобы быть добрым, нужно быть жестоким.
- Все становится еще хуже, прежде чем станет лучше.
- Единственное правило — игнорировать все правила.
Каламбур
Каламбур — это фигура речи, которая содержит «игру» слов, например, использование слов, которые означают одно, для обозначения другого или слов, которые звучат одинаково, в качестве средства изменения значения.
- Спящий бык называется бульдозером.
- Бейсболисты едят на домашней тарелке.
- Белые медведи голосуют на Северном избирательном участке.
- Рыбы умны, потому что они ходят стаями.
- Один медведь сказал другому, что жизнь без них была бы гризли.
Оксюморон
Оксюморон — это фигура речи, которая соединяет две противоположные идеи, обычно в фразах из двух слов, для создания противоречивого эффекта.
- открытый секрет
- в одиночку вместе
- правда ложь
- контролируемый хаос
- довольно уродливые
общие примеры фигуры речи в письме
писатели также используют фигуры речи в письменной форме
значение.Вот несколько распространенных примеров фигур речи, используемых в письменной форме:
Сравнение
Сравнение — это фигура речи, в которой две непохожие вещи сравниваются друг с другом, используя термины «подобно» или «как».
- Она такая красивая, как картинка.
- Я очень доволен.
- Он силен как бык.
- Ты хитер, как лиса.
- Я счастлив как моллюск.
Метафора
Метафора — это фигура речи, которая сравнивает две разные вещи без использования терминов «подобно» или «как».”
- Он как рыба в воде.
- Она звезда на небе.
- Мои внуки — цветы моего сада.
- Эта история — музыка для моих ушей.
- Ваши слова — заезженная пластинка.
Эвфемизм
Эвфемизм — это фигура речи, относящаяся к образному языку, предназначенная для замены слов или фраз, которые иначе считались бы резкими, невежливыми или неприятными.
- Прошлой ночью дедушка Джо скончался (умер).
- Она начала чувствовать себя выше холма (старый).
- Молодые люди интересуются птицами и пчелами (секс).
- Мне нужно припудрить нос (иди в ванную).
- Наша компания приняла решение отпустить вас (уволить).
Олицетворение
Олицетворение — это фигура речи, приписывающая человеческие качества чему-то, что не является человеком.
- Я слышал свист ветра.
- Вода плясала по моему окну.
- Моя собака говорит мне начинать обедать.
- Луна улыбается мне.
- На заднем фоне гудел ее будильник.
Написание фигур речи
Как литературный прием, фигуры речи усиливают значение написанных и произнесенных слов. В устном общении фигуры речи могут прояснить, улучшить описание и создать интересное использование языка.
В письменной речи, когда фигуры речи используются эффективно, эти приемы улучшают способность писателя к описанию и выражению, так что читатели лучше понимают, что передается.
Важно, чтобы писатели конструировали эффективные обороты речи, чтобы смысл не был потерян для читателя. Другими словами, простая перестановка или сопоставление слов не так эффективна, как преднамеренная формулировка и фразировка. Например, гипербола «Я мог бы съесть лошадь» эффективно показывает сильный голод, используя образный язык. Если бы писатель попробовал гиперболу «Я мог бы съесть амбар из солодки», образный язык неэффективен, и смысл был бы потерян для большинства читателей.
Вот несколько способов, которыми писатели могут извлечь выгоду из использования фигур речи в своих произведениях:
Фигура речи как художественное использование языка
Эффективное использование фигур речи является одним из величайших проявлений художественного использования языка. Способность создавать поэтический смысл, сравнения и выражения с помощью этих литературных приемов — вот как писатели формируют искусство с помощью слов.
Образ речи как развлечение для читателя
Эффективные обороты речи часто повышают развлекательную ценность литературного произведения для читателя.Многие фигуры речи вызывают чувство юмора или вызывают чувство иронии, чего не делают буквальные выражения. Это может вызвать у читателя большее чувство вовлеченности, когда дело доходит до литературного произведения.
Образ речи как памятный опыт для читателя
Используя эффективные обороты речи для улучшения описания и значения, писатели делают свои произведения более запоминающимися для читателей как опыт. Писатели часто могут поделиться трудной истиной или передать определенную концепцию образным языком, чтобы читатель лучше понял материал и остался в памяти.
Примеры фигур речи в литературе
В литературных произведениях используется бесчисленное множество фигур речи, которые используются в качестве литературных приемов. Эти фигуры речи придают смысл литературе и демонстрируют силу и красоту образного языка.
Вот несколько примеров фигур речи в известных литературных произведениях:
Пример 1:
Великий Гэтсби (Ф. Скотт Фицджеральд)В его голубых садах мужчины и девушки приходили и уходили, как мотыльки среди шепота и шампанское и звезды.
Фицджеральд использует здесь сравнение как фигуру речи, чтобы сравнить гостей вечеринки Гэтсби с мотыльками. Образы, используемые Фицджеральдом, отличаются изысканностью и красотой и создают эфемерную атмосферу. Однако сравнение гостей Гэтсби с мотыльками также укрепляет идею о том, что их привлекают только ощущения вечеринок и что они уйдут, не оказав никакого реального влияния или связи. Это сравнение, как фигура речи, подчеркивает в романе темы поверхностности и мимолетности.
Пример 2:
Сто лет одиночества (Габриэль Гарсиа Маркес)Оба описали одновременно, что там всегда был март и всегда понедельник, а потом они поняли, что Хосе Аркадио Буэндиа не такой сумасшедший, как семья, но что он был единственным, у кого было достаточно ясности, чтобы ощутить истину того факта, что время тоже спотыкается и имеет случайности и поэтому может расколоться и оставить увековеченный фрагмент в комнате.
В этом отрывке Гарсия Маркес использует олицетворение как фигуру речи.Время персонифицируется как сущность, которая «спотыкалась» и «попадала в аварии». Это эффективное использование образного языка, поскольку это олицетворение времени указывает на уровень человеческой слабости, который редко ассоциируется с чем-то столь измеренным. Кроме того, это эффективно в романе как фигура речи, потому что время имеет большое влияние на сюжет и персонажей рассказа. Олицетворенное таким образом, значение времени в романе усиливается до такой степени, что оно становится персонажем само по себе.
Пример 3:
по Фаренгейту 451 (Рэй Брэдбери)Книга – это заряженное ружье в соседнем доме… Кто знает, кто может стать целью начитанного человека?
В этом отрывке Брэдбери использует метафору как фигуру речи, чтобы сравнить книгу с заряженным ружьем. Это эффективный литературный прием для этого романа, потому что в этой истории книги считаются оружием свободы мысли, и владение ими является незаконным.
сообщите об этом объявленииКонечно, Брэдбери утверждает, что книга — это заряженное ружье только как средство переносного, а не буквального значения.Эта метафора особенно сильна, потому что сравнение маловероятно; книги вообще не считаются опасным оружием. Тем не менее, сравнение имеет определенный уровень логики в контексте истории, в которой стремление к знаниям используется как оружие и криминализовано.
Что такое конгруэнтные фигуры? — Определение и примеры — Видео и стенограмма урока
Примеры конгруэнтности
Конгруэнтность — это то, что имеют две фигуры, если они конгруэнтны.Эти фигуры явно совпадают, потому что они абсолютно одинаковы:
Та же форма, тот же размер. Они конгруэнтны! А как насчет этих форм?
Один треугольник указывает вверх, а другой вниз.
Однако, если бы вы их измерили, вы бы обнаружили, что соответствующие стороны обоих треугольников совершенно одинаковы. На самом деле второй треугольник такой же, как и первый; его просто повернули.Значит, эти фигуры равны.
Важно помнить, что направления граней фигур не влияют на их конгруэнтность. Пока они имеют одинаковую форму и одинаковые размеры, они конгруэнтны.
Теперь посмотрим на квадраты:
Это оба квадрата, но один намного меньше другого. Хотя они одинаковой формы, эти две фигуры разного размера. Следовательно, эти квадраты неконгруэнтны или не конгруэнтны.
Последний пример:
Хотя эти фигуры не совсем те формы, которые мы привыкли видеть, они состоят из одних и тех же линий и кривых и имеют одинаковый размер. Единственная разница в том, что одно является отражением другого, но они по-прежнему конгруэнтны, поскольку имеют одинаковые формы и размеры.
Резюме урока
Любые фигуры (даже если их больше двух) одинаковой формы и размера конгруэнтны .Неважно, смотрят ли они в разные стороны или одно является отражением другого. Пока форма и размер в точности одинаковы, фигуры конгруэнтны.
Словарь конгруэнтных фигур и определения
Словарь Определения Конгруэнтность фигуры, даже если они отражены или повернуты, но имеют одинаковую форму и размер Несоответствие фигурки, которые отличаются по размеру, форме или тому и другому Конгруэнтность что имеют две фигуры, если они конгруэнтны Результаты обучения
По завершении этого урока учащиеся готовы:
- Описывать конгруэнтные фигуры
- Знать, как определить конгруэнтность
- Определите, когда формы несовместимы
цифра-n
цифра-nSense Number 1: двухмерное представление, рисунок, иллюстрация, шаблон проектирования
Комментарий: РИСУНОК [+физический][+представление][+2D]
Примеры:
На этом рисунке показано изменение доходов за последние двенадцать кварталов.
Рисунки в книге помогут более наглядно объяснить процесс.
Дети рисовали фигуры треугольников, окружностей, парабол и параллелограммов.
Сьюзен нарисовала фигурки птиц и цветов на стене моей столовой.
Петроглифы представляли собой фигуры из палочек и круги, нарисованные на вулканических породах.Сопоставления:
WordNet 3.0 Смысловые числа: 1, 6, 12Чувство номер 2: тело или форма, наблюдаемая неповрежденная сущность
Комментарий: РИСУНОК[+физический][+тело][+существующий]
ПРИМЕЧАНИЕ: фигура НЕ подразумевает ссылку на какую-то отдельную сущность, она -есть- сущность.Примеры:
Джон считает, что у Мэри прекрасная фигура.
Из глубин за рифом вынырнула фигура большой белой акулы.
Они помнят фигуру человека, стоящего в тени возле библиотеки.
Фигуры голодающих детей из поездки за границу до сих пор не давали ей покоя.Сопоставления:
WordNet 3.0 Смысловые числа: 2, 11
Смысловое число 3: количество, выраженное числом
Комментарий: ЦИФРА[+количество][+число]
Примеры:
Я собираюсь написать число от одного до десяти, а вы должны угадать, какое именно.
Бухгалтерская фирма подтвердила, что данные за прошлый год верны.
Он назвал мне цифру в две тысячи долларов.
Прогнозируемые цифры дефицита больше, чем ожидалось.Сопоставления:
WordNet 3.0 Смысловые числа: 3, 7, 9Чувство номер 4: трехмерное представление тела
Комментарий: РИСУНОК[+физический][+представление][+3D][+модель]
ПРИМЕЧАНИЕ: фигура подразумевает ссылку на какой-то другой объект, на котором она смоделирована.Примеры:
Салли сделала красивую фигурку лошади из глины.
Они изучают объемные фигуры на уроке геометрии.
Его литые бронзовые фигуры обнаженных тел являются одними из самых известных.
Она дала детям поиграть с стеклянными фигурками животных.
Мы любовались конечными фигурами львов на старых римских колоннах.
Эти восковые фигуры кажутся мне слишком реальными.Сопоставления:
WordNet 3.0 Sense Numbers: 4Число чувств 5: влиятельное или известное лицо
Комментарий: ФИГУРА[+человек][+влиятельный]
Примеры:
В течение многих лет он был важной фигурой в общественной политике.
Мэри не нравится быть авторитетной фигурой в своей компании.
Читаем о великих литературных деятелях девятнадцатого века.
Ребенок смотрел на Джона как на отца.
Старый профессор был любимцем в кампусе.Сопоставления:
WordNet 3.0 Sense Numbers: 5Чувство номер 6: метафорический литературный прием, троп
Комментарий: РИСУНОК[+язык][+устройство][+метафора]
Примеры:
Иностранец не понял всех фигур речи, которые мы использовали.
«Легко, как пирог» — это фигура речи.
Сопоставления:
WordNet 3.0 Sense Numbers: 10Чувство номер 7: впечатление или общее качество, которым обладает что-то
Комментарий: ФИГУРА[+качество][+впечатление][+восприятие]
ПРИМЕЧАНИЕ: Это может быть метафорическим расширением Sense 2Примеры:
Разве они не выглядят красиво на танцполе?
Джон в своем альпинистском снаряжении представляет собой довольно суровую фигуру.
Должно быть, я был жалкой фигурой, вползшей в отель, весь мокрый и грязный.Сопоставления:
WordNet 3.0 Sense Numbers: 8Чувство номер 8: последовательность движений или жестов во времени
Комментарий: ФИГУРА[+активность][+движение][+последовательность]
Примеры:
Новая танцовщица прекрасно исполняла фигуры во время прослушивания.
В соревновании фигуристы должны составить четыре разных комплекта фигур.
Она лучшая фигуристка в мире.
Эти пять нот составляют фигуру трехтактной мелодииОтображения:
WordNet 3.0 Sense Numbers: 13
Фигурки Toy Company
Серия фигурок «Восходящие звезды рестлинга»: набор из 12 фигурок
Рекомендованная производителем розничная цена: $359,88
Цена: $299,99
Вы экономите: 17 %
Количество:
* Всего толькоФигурки Legends of Professional Wrestling Series: набор из 12 фигурок
Рекомендованная производителем розничная цена: 359 долларов.88
Цена: $299,99
Вы экономите: 17 %
Количество:
* Всего толькоСерия 8-дюймовых фигурок президентов США: набор из 12 фигурок
Рекомендованная производителем розничная цена: $359,88
Цена: $299,99
Вы экономите: 17 %
Количество:
* Всего толькоСерия 6-дюймовых фигурок DC Comics Retro: набор из всех 6 фигурок Дуэлы Дент [в фабричных сумках]
Цена: 79 долларов.
99
Количество:
* Всего толькоRising Stars of Wrestling Series: Итан Пейдж
Цена: $29,99
Количество:
* Всего толькоВосходящие звезды рестлинга: Эли Дрейк
Цена: 29 долларов.99
Количество:
* Всего толькоФигурки из серии Legends of Professional Wrestling : Алекс Райт
Цена: $29,99
Количество:
* Всего толькоФигурки из серии «Новые приключения Бэтмена»: Бэтмен [в фабричной сумке]
Цена: 29 долларов.99
Количество:
* Всего толькоФигурки из серии «Новые приключения Бэтмена»: Джокер [в фабричной сумке]
Цена: $29,99
Количество:
* Всего толькоФигурки из серии «Новые приключения Бэтмена»: Риддлер [в фабричной сумке]
Цена: 29 долларов.
99
Количество:
* Всего толькоDC Comics Retro 8-дюймовые фигурки: новая скульптура головы Супермена [свободно в фабричной сумке]
Цена: $19,99
Количество:
* Всего толькоСерия фигурок Ring of Honor Wrestling: Rush
Цена: 29 долларов.99
Количество:
* Всего толькоСерия фигурок Ring of Honor Wrestling: PCO
Цена: $29,99
Количество:
* Всего толькоОбезьяны 8-дюймовые фигурки серии One Red Band Наряд: Микки Доленц
Цена: 29 долларов.99
Количество:
* Всего толькоОбезьяны 8-дюймовые фигурки серии One Red Band Наряд: Майк Несмит
Цена: $29,99
Количество:
* Всего толькоОбезьяны 8-дюймовые фигурки серии One Red Band Наряд: Дэви Джонс
Цена: 29 долларов.
99
Количество:
* Всего толькоОбезьяны 8-дюймовые фигурки серии One Red Band Наряд: Питер Торк
Цена: $29,99
Количество:
* Всего толькоОбезьяны 8-дюймовые фигурки серии One Red Band Outfit: набор из всех 4
Цена: 119 долларов.96
Количество:
* Всего толькоОбезьяны 8-дюймовые фигурки: синяя лента Наряд: Микки Доленц
Цена: $29,99
Количество:
* Всего только8-дюймовые фигурки обезьян: синяя лента, наряд: Майк Несмит
Цена: 29 долларов.99
Количество:
* Всего только8-дюймовые фигурки обезьян: синяя лента, наряд: Дэви Джонс
Цена: $29,99
Количество:
* Всего только8-дюймовые фигурки The Monkees: синяя лента.
Наряд: Peter Tork .
Цена: 29 долларов.99
Количество:
* Всего только8-дюймовые фигурки обезьян: синяя лента, костюм: набор из всех 4
Цена: $119,96
Количество:
* Всего толькоСерия 12-дюймовых ретро-фигурок DC Comics: выберите любую 10
Цена: 219 долларов.99
Выберите свою собственную фигурку DC Comics в штучной упаковке в стиле ретро, 8 дюймов, с телом S-типа
Цена: $39,99
DC Comics в штучной упаковке ретро 8-дюймовые фигурки с телом типа S: Бэтмен
Цена: 39 долларов.99
Количество:
* Всего толькоDC Comics в штучной упаковке ретро 8-дюймовые фигурки с телом типа S: Робин
Цена: $39,99
Количество:
* Всего толькоDC Comics в штучной упаковке ретро 8-дюймовые фигурки с телом типа S: Супермен
Цена: 39 долларов.
99
Количество:
* Всего толькоDC Comics в штучной упаковке 8-дюймовые фигурки в стиле ретро с телом типа S: Супермен [новая скульптура головы]
Цена: $39,99
Количество:
* Всего толькоDC Comics в штучной упаковке ретро 8-дюймовые фигурки с телом типа S: Бэтмен [съемный капюшон]
Цена: 39 долларов.99
Количество:
* Всего толькоDC Comics в штучной упаковке ретро 8-дюймовые фигурки с телом типа S: Робин [съемная маска]
Цена: $39,99
Количество:
* Всего толькоПолноцветная 3D-печатная статуя бюста президента Дональда Трампа
Цена: от 34 долларов.95
3D-печатная полноцветная статуя бюста президента Джо Байдена коллекционная
Цена: от $34,95
Полноцветная 3D-печатная статуя бюста президента Джона Ф.
Кеннеди, коллекционная
Цена: от 34 долларов.95
Серия 8-дюймовых фигурок DC Comics Retro: Outsider Halo [свободно в фабричной сумке]
Цена: $29,99
Количество:
* Всего толькоDC Comics Retro Style 8-дюймовые фигурки в коробке: Зеленая стрела [Лига справедливости]
Цена: 26 долларов.99
Количество:
* Всего только
Фигуры речи (полный список)
Техники > Использование языка > Фигуры речи > Полный список
Фигуры речи (или «риторические тропы») — это способы использования слов, которые могут показаться необычными, но имеют конкретный и желаемый эффект.Читать как «обычные слова», они часто нарушают норму правила грамматики, но тем не менее их можно понять. Они распространены в поэзии.
и красноречивая речь.
«Фигуры речи» часто используются в общем, и большой список здесь включает не только фигуры речи, но и более широкий диапазон риторических и языковых средств.
- Аббасер: См. Тапиноз.
- Абусио: См. Катахрезу
- Аколута: Взаимная замена слов.
- Акцизм: Притворный отказ от желаемого.
- Accumulatio: сведение очков в мощную кульминацию.
- Acutezza: остроумие или игра слов.
- Акирон: Использование слова, противоположного тому, что имеется в виду.
- Adianoeta: Выражение, имеющее второе, тонкое значение.
- Дополнение: Помещение глагола в начало.
- Адинатон: Преувеличенное заявление о невозможности.
- Астеисмос: Вежливое выражение эмоций.
- Этиология: Заявление с подтверждающей причиной.
- Affirmatio: Говорить так, как будто чья-то точка зрения оспаривается.
- Аганактез: Возмущенный возглас.
- Аллегория: Повествование с использованием устойчивой метафоры.
- Аллеотета: Замена одного на другое.
- Аллюзия: Косвенная ссылка.
- Аллитерация: повторение одного и того же исходного звука.
- Засада: См. Перифраз.
- Амфибология: Неоднозначность в грамматике.
- Амфилогия: многословие во избежание причинения вреда себя.
- Ampliatio: Использование имени там, где оно не определено.
- Amplificatio: Общее усиление аргумента.
- Анабасис: Ступенчатое усиление ударения.
- Анацефалез: сводка известных фактов.
- Anacoenosis: Запрос мнения аудитории, чтобы узнать соглашение.
- Anacoloutha: невзаимное слово замена.
- Анаколутон: Окончание предложения отличается от ожидаемого.
- Анакрус: Безударные слоги в начале.
- Анадиплозис: Повторение последнего слова в начале следующего предложения.
- Аналогия: A равно , как B.
Использование одного для описания другого.
- Анамнез: Эмоциональный отзыв.
- Анангеон: Оправдание, основанное на необходимости.
- Анафора: Повторение начальных слов.
- Анаподотон: опущен пункт для преднамеренного эффект.
- Анастрофа: Изменение нормального порядка слов.
- Анезис: добавление заключения, сокращающего сказанное.
- Antanaclasis: Повторение одного и того же слова с изменением значения.
- Антанагог: положительно относиться к чему-то отрицательному.
- Антимерия: Замена одной части речи на другую.
- Антилогия: См. Антанакласис.
- Антиметабол: повторяющийся пункт, обратный порядок слов.
- Антипофора: Спрашивать, а потом отвечать на свои вопросы.
- Antiphrasis: Использование слов в противоположном смысле для иронии.
- Antiptosis: два логичных, но противоречивых аргумента.
- Антирезис: Отказ от плохого аргумента.
- Антистекон: Замена одного элемента слова.
- Антистрофа: Повторение последнего слова в последовательных фразах.
- Антитезис: противопоставление противоположности.
- Антономазия: Называть человека не свое имя.
- Апкопе: пропуск букв в конце слова.
- Аферез: Пропуск букв в начале слова.
- Афоризм: Вопрос о значении слово.
- Апофаза: Говорить о чем-то без упоминание об этом.
- Апория: Притворное сомнение.
- Апосиопезис: Незаконченное предложение.
- Апостроф: «в сторону» для других.
- Приложение: Многоуровневое значение.
- Архаизм: Использование устаревшего языка.
- Ассонанс: Повторение одного и того же гласного звука.
- Asterismos: добавление слова для ударения следующие слова.
- Асиндетон: Опускание союзов.
- Ауреация: Использование красивых слов.
- Автоклесис: представление предмета путем отказа от его обсуждения.
- Ауксезис: Повышение важности.
- Бделигмия: Выражение презрения или ненависти.
- Bomphiologia: Напыщенная, хвастливая речь.
- Брахиология: сокращенное выражение.
- Brevitas: краткое выражение.
- Cacemphaton: Заведомо дурно звучащее выражение.
- Какофония: Резкое сочетание слов.
- Катабазис: Неуклонно уменьшающийся акцент.
- Катахреза: Неправильное использование слов.
- Катафора: Использование слова для обозначения слова, которое будет использовано позже.
- Категория: Прямое разоблачение чужого недостатки.
- Хиазм: Две фразы с переворотом во второй.
- Кледонизм: многословие, чтобы не говорить неудачные слова.
- Кульминация: Слова упорядочены по возрастанию.
- Congeries: см. Accumulatio.
- Созвучие: Повторение согласных звуков.
- Correctio: Исправление для пересмотра значения.
- Crasis: Сокращение двух гласных в более длинный звук.
- Диакопа: Повторение слова после одного или двух других слов.
- Diallage: несколько аргументов для установления одной точки.
- Distinctio: Описание чего-либо, говоря, чем оно не является.
- Dubitatio: См. Апорию.
- Дисфемизм: Замена мягкого слова более сильным.
- Дисритмия: Нарушение ритмического паттерна.
- Дистмезис: Вставка одного слова в середину другого.
- Экфонезис: Короткий восклицательный знак.
- Многоточие: опущение слов, делающих предложение ясным.
- Enallage: замена одного предмета другим.
- Enjambment: Разрыв фразы в случайном порядке точка.
- Enumeratio: Разбивка и детализация предмет.
- Эпаналепсис: Повторение одной и той же фразы в начать и закончить.
- Эпанадос: Повторение слов в обратном порядке приказ.
- Эпанортоз: Исправление в предложении.
- Эпентезис: добавление букв в середину слова.
- Эпистрофа: повторение одного и того же последнего слова или фразы.
- Эпитроп: уступать, чтобы получить.
- Эпизевксис: Повторение слова с жаром.
- Эротема: Риторический вопрос.
- Эфиопейя: Поставить себя на место другого.
- Euche: Выражение эмоций через молитву.
- Эвфемизм: замена оскорбительных слов нежными.
- Эвсистолизм: Использование инициалов, чтобы не говорить резких слов.
- Exemplum: Использование примеров (реальных или вымышленных).
- Exergasia: Повторение точки в разных слова.
- Экстрапозиция: Помещение субъекта в более позднее положение, чем обычно.
- Вымысел: Приписывание человеческих черт существам.
- Глоссолалия: Сфабрикованная, бессмысленная речь.
- Градация: См. Кульминация.
- Хендиадис: Два слова, соединенных союзом.
- Гетерозис: Изменение формы глагола.
- Homoioteleuton: сходные окончания в соседних или параллельных словах.
- Гомофон: разные слова, которые звучат такой же.
- Гипаллаж: изменение синтаксического отношения.
- Hyperbaton: Разделение слов, которые принадлежат друг к другу.
- Гипербола: Преднамеренное преувеличение.
- Гипокатастаз: Подразумеваемое сравнение.
- Гипокоризм: Использование ласкательных имен, уменьшительно-ласкательных, детский лепет.
- Hypophora: см. Anthypophora.
- Гипотаксис: Подчинение предложений для показа отношения.
- Hypozeuxis: Каждое предложение имеет свое собственное подлежащее и глагол.
- Hysteron proteron: изменение времени последовательность, чтобы поставить ключевые вещи на первое место.
- Илеизм: Обращение к себе в третьем лице.
- Inclusio: Закрепление прохода одинаковым слова.
- Намек: Косвенный намек.
- Ирония: сказать что-то, используя противоположное.
- Изоколон: Фразы с несколькими сходствами.
- Кеннинг: Замена существительного на иносказания мифологизация.
- Колакейя: Лесть для отвлечения внимания от нежелательных элементов.
- Litotes: Отрицание противоположного тому, что утверждается.
- Малапропизм: замена слова похожим по звучанию.
- Мейоз: Преуменьшение для акцента или эффекта.
- Меризм: Комбинирование слов для значения, выходящего за рамки обычного сочетания.
- Меризм: Полное описание или ссылка.
- Металепсис: ссылка на что-то через слабо связанный элемент.
- Метафора: — это Б. Использование одного для описания другого.
- Метаплазмус: преднамеренная опечатка.
- Метатезис: Перестановка букв в слове.
- Метонимия: Использование одного предмета для представления другого.
- Повествование: Представление существенных фактов.
- Носизм: Отношение к себе во множественном числе.
- Oeonismos: выражение эмоций через желание или надеясь.
- Оптатио: Восклицание желания.
- Оксюморон: Соседние слова, которые кажутся противоречащими друг другу.
- Parachesis: повторение одного и того же звука в последовательные слова.
- Paradeigma: Список примеров для обобщения.
- Paradiastole: Изображение порока как добродетели.
- Парадокс: кажущееся противоречие.
- Paraeneticon: Выражение эмоций через увещевание.
- Паралипсис: выделение явным пропуском.
- Параллелизм: повторяющиеся шаблоны в приговор.
- Парапросдокиан: Удивительная концовка.
- Паратаксис: последовательные независимые предложения.
- Парегменон: Повторение слов тот же корень.
- Скобки: Вложение предложения.
- Парисология: преднамеренное использование двусмысленных слов.
- Parison: Сопоставление шаблонов между структурами.
- Parisosis: одинаковое количество слогов в пункт.
- Паремион: Чрезмерная аллитерация.
- Паромойоз. Одинаковые звуки в двух оговорки.
- Парономазия: использование слов со схожим звучанием.
- Парресия: Смелость речи.
- Перифраза: Круговая формулировка.
- Perissologia: Чрезмерное использование слов.
- Персонификация: Придание объекту человеческих характеристик.
- Плеоназм: Использование ненужных слов.
- Место: Повторение слова при изменении специфика.
- Полиптотон: Повторение слова в разных формах.
- Полисиндетон: Повторяющиеся союзы.
- Полиптотон: Повторение в разных формах.
- Praecisio: Не говорить, чтобы преодолеть сообщение.
- Praegnans Constructionio: См. Брахиология.
- Praeteritio: Упоминание того, что есть против правил.
- Прокаталепсис: Заранее отвечать на возражения.
- Пролепсис: Ожидание действия.
- Пропаралепсис: Добавление букв в конец слова.
- Протез: Добавление букв в начале слова.
- Пословица: Инкапсулированный и бесспорный мудрость.
- Пситтацизм: попугайное повторение.
- Каламбур: игра слов.
- Repetitio: Повторение одного слова.
- Рифма: Повторение звуков в конце слов.
- Scesis onamaton: опускание единственного глагол.
- Sententia: Цитирование мудрости для создания истины.
- Simile: явное сравнение двух вещей.
- Спунеризм: замена начальных букв двух слов.
- Subreption: Формулировка слов для искажения и сокрытия фактов.
- Syllepsis: См. Zeugma.
- Symploce: Одновременное использование анафоры и эпистрофы.
- Synaloepha: пропуск одной гласной для объединения двух слов.
- Synchysis: Запутанное расположение слов.
- Обморок: Сокращение слова за счет пропуска среднего сегмента.
- Syndeton: Использование союзов.
- Синекдоха: Понимание одного с другим.
- Синезис: Объединение вещей.
- Synizesis: Последовательно звучащие гласные.
- Синонимия: Повторяющиеся синонимы для усиление.
- Тапиноз: Преуменьшение и уменьшение чего-либо.
- Тавтология: Повторение значения без необходимости.
- Тмесис: Вставка одного слова в середину другого.
- Transumptio: См. Металепсис.
- Tricolon: Три компонента, увеличивающие мощность.
- Zeugma: Два слова связаны с другим, только одно уместно.
Это четыре классические классификации фигур речи, которые изменяют текст: добавление, опущение, замена и расположение.Часто это имеет большое значение где эти модификации происходят, в начале, середине или конце слова, фраза или предложение.
В некотором смысле этот список несколько преувеличен в использовании термина «цифра» для описать все. На самом деле многие из них на самом деле являются скорее устройствами, чем цифрами. Но потом «фигура речи» обычно используется для обозначения многих форм и была принята таким образом здесь.
См. также
Что такое цифры?, заблуждения, Рассказывание историй
Практические советы по подписям к рисункам и таблицам для рукописей
Написание рукописи является неотъемлемой частью обмена результатами исследований.Авторы пишут и публикуют рукописи, ориентированные на определенную аудиторию журнала. Рукопись, представляющая исходные данные исследования, содержит различные разделы, а именно введение, методы, результаты, обсуждение и выводы. Обычно рисунки и таблицы представляют сложные данные визуально в разделе результатов рукописи. Как читатели понимают информацию, переданную вашей таблицей или рисунком? Ответ прост. Они смотрят на рисунки/таблицы и на соответствующие легенды.
Подписи или подписи объясняют рисунки, таблицы или изображения в рукописи.
Как известно, использование рисунков и таблиц в научных работах служит цели наглядного описания предмета исследования.
Точно так же легенды или подписи предоставляют описательную информацию о рисунках или таблицах.
Легенды должны удовлетворять этим двум основным требованиям:
- Помогите читателям понять значение рисунка или таблицы.
- Помогите интерпретировать значение основных результатов.
При написании легенд ученики часто сталкиваются со следующими сомнениями:
- Из чего должны состоять легенды и как их структурировать?
- Где появляются легенды в рукописи или техническом отчете?
Поэтому мы предлагаем краткое руководство по написанию описательных подписей к рисункам и таблицам, также известных как подписи.
Подписи к рисункам и таблицам
В рукописи или отчете сопровождающие таблицы и рисунки отображают количественную информацию. Цель состоит в том, чтобы представить данные визуально, чтобы читатели могли легко понять техническую информацию и контекст. Всегда рекомендуется использовать различные типы форматов представления данных (таблицы, графики данных, точечные диаграммы, рисунки и т.
д.) при описании больших объемов данных.
Обязательно учитывайте следующие моменты при написании легенд в рукописи или плакате.
- Поместите подписи над таблицей и выровняйте их по левому краю (обычно). Таблицы читаются сверху вниз и должны быть пронумерованы. Например, Таблица 1.
- Не забывайте заканчивать название рисунка точкой. Не используйте двоеточие, точку с запятой или запятую. Например, Рисунок XYZ.
- Разместите подписи под рисунком. Рисунки могут быть представлены в виде графиков, изображений или схематических диаграмм и обычно читаются снизу вверх.
- Используйте заголовки как для рисунков, так и для графиков на слайдах и плакатах устных презентаций.
- Подписи требуют номера рисунка/таблицы, названия и другой пояснительной информации, если это необходимо.
- В идеале не превышайте ограничение в 350 слов для каждой подписи к фигуре.
- При необходимости цитируйте данные из других публикаций в подписях.
- Иметь четкое представление о концепции, связанной с экспериментом.
- Упорядочить информацию логически.
- Укажите измеренные единицы данных, включая концентрации, средние измерения и значимые значения, если это необходимо.
Основные характеристики легенды о хорошей фигуре
Название – Дайте краткое название, относящееся ко всей фигуре. Он может быть либо описательным (изложением процесса или типа анализа эксперимента), либо декларативным (изложением основных выводов или обобщением результатов эксперимента).
Материалы и методы – В этом разделе описываются методы, использованные в эксперименте. Следует ограничиться той информацией, которая абсолютно необходима для понимания рисунка.
Результаты — Оператор результата должен использоваться, если заголовок является описательным. Не указывайте результаты, если вы дали декларативное название легенде рисунка. Это может варьироваться не только в разных статьях, но и в разных журналах.
Определения – Это объяснение особенностей фигуры. Это включает описание символов, узоров, линий, цветов, нестандартных сокращений, масштабных линеек и планок погрешностей, которые являются частью рисунка. Вы можете исключить элементы, которые уже описаны на фактическом рисунке.
Подписи или легенды должны рассказывать историю
Подписи в рукописи (или отчете) рассказывают читателю историю о рисунках или таблицах. Для эффективного написания подписи используйте следующий контрольный список:
- Подписи должны быть краткими, но при этом давать исчерпывающее объяснение данных в том виде, в каком они появляются в тексте.
- Прошедшее время часто используется для описания завершенных экспериментов, тогда как настоящее время может использоваться для передачи фактического утверждения, основанного на результатах вашего эксперимента.
- Подписи должны говорить сами за себя и предоставлять читателям достаточную информацию без ссылки на соответствующий текст в рукописи.
- Он должен включать информацию о важных аспектах, таких как описание (тип эксперимента), использованный метод или методика (размер выборки, тип используемой животной модели, исследуемые условия и т. д.) и полученный результат (p-значение).
- Подписи должны быть написаны полным предложением, начиная с общепринятых заглавных букв.
- Это должно быть руководство, помогающее читателю понять и найти данные, которые он ищет в рукописи.
- Он должен четко объяснять контекст данных.
- При необходимости заголовок должен содержать единицы измерения, представляющие тип данных, продолжительность эксперимента и т. д.
- Размер шрифта заголовка должен быть меньше размера текста в документе.
- Заголовок должен быть выровнен по левому краю таблицы или графика.
Тем не менее, не забудьте проверить правила для авторов вашего целевого журнала на предмет последних двух пунктов!
Рассмотрим примеры хорошо написанных подписей к таблицам и рисункам.
(Источник: https://www.overleaf.com/16744469whjwcjmcgxtw#/64164224/)
(Источник: https://www.overleaf.com/16744374kttvywpdqyby#/64163939/)
Как вы пишете подписи к рисункам или таблицам в своей рукописи? Какие вещи вы держите в уме для ясного и краткого описания? Поделитесь с нами в разделе комментариев ниже некоторыми из ваших замечаний по форматированию рукописи!
27 фигур речи в мультфильме
Сможете ли вы найти 27 фигур речи в этом мультфильме?
Наш английский язык богат буквальными и образными выражениями.Но что такое фигура речи?
Это риторический прием, который писатель или оратор намеренно использует для создания подразумеваемого сравнения со словом или фразой.
Обычная фигура речи часто использует неодушевленный предмет для передачи переносного значения вместо буквального.
Каждый день мы используем множество фигур речи
Я уверен, вы знаете выражение a ll the world’s a stage Уильяма Шекспира.
Мир — это не сцена, где мужчины и женщины разыгрывают спектакли.
Шекспир использует слово «стадия», чтобы дать абстрактное значение тому, как мы все живем и ведем себя в нашем мире.
Очень часто мы также используем сравнения и метафоры, чтобы выразить идею или понятие.
Идиомы — еще один тип образной речи.
Мы используем тысячи образных выражений в нашем повседневном языке.
Распространенные примеры фигур речи
Мы часто используем неодушевленный предмет в качестве подразумеваемого сравнения в фигуре речи.
Помогает расставить акценты. Например, идет дождь из кошек и собак, и я тебе помогу .
Животные не падают с неба. И руку топором не отрубишь, чтобы кому-то отдать.
Оба эти выражения — игра слов.
Эти две образные языковые фразы буквально означают, что идет очень сильный дождь, и я с радостью помогу вам .
Если вы писатель или писатель, вы все время используете слова и выражения, как в прямом, так и в переносном смысле.
Возможно, вы пытаетесь создать словесную иронию, выразить человеческие качества или добавить красок в свой текст.
Типы выражений в народных оборотах
Наиболее распространенными литературными приемами являются метафоры и сравнения, которые являются хорошо известными образными выражениями.
Другой тип образной формы использует повторение порядка слов или подобные последовательные предложения, такие как в неправильном месте в неправильное время.
Другие риторические приемы могут использовать хиазм, когда вторая часть выражения уравновешивается первой.Например, нужно работать, чтобы жить, а не жить, чтобы работать.
Преувеличение или гипербола в литературных терминах может быстро превратить слово или фразу из буквального языка в образный. Он намеренно делает ситуацию значимой.
У меня сегодня миллион дел в офисе , или это стоило мне руки и ноги.
Противоположное, конечно, преуменьшение, которое делает ситуацию менее важной.
Это всего лишь царапина , когда речь идет о глубокой или неприятной ране. Или сегодня немного свежо когда температура значительно ниже нуля. Или, Тайгер Вудс был почти приличным игроком в гольф в расцвете сил .
Другие формы
Многие примеры фигур речи включают эвфемизмы.
Это очень распространенная форма высказывания чего-либо в более вежливой или не такой прямолинейной манере.
Он скончался вместо того, чтобы умереть. Я отпущу тебя взамен твоего увольнения. Или он выпал из кузова грузовика , хотя на самом деле он был украден.
В некоторых выражениях используется аллитерация, когда согласный звук повторяется.
Например, Я занят как пчела, и он мертв как дверной гвоздь или додо .
Одним из моих любимых источников идиом и выражений является мой любимый вид спорта – крикет.
Быть сбитым на шесть, попасться на липкую калитку, попасть в тупик, я сделал это сам, попасться , и забить девицу над . Мне нравится последний.
Вы все это знаете, так что мне не нужно напоминать вам об идиоматической речи. Мы используем фразу с объектом для создания подразумеваемого или абстрактного значения.
Я знаю, что ты знаешь, но прежде чем ты исчезнешь в эфире…
Насколько хорошо ты знаешь обороты речи?
Вот увлекательное задание, которое поможет вам проверить свои знания идиоматической и образной речи.
Я наткнулся на эту совершенно блестящую карикатуру Эллы Барон в литературном приложении Times в Твиттере.
Элла проиллюстрировала двадцать семь терминов образного языка.
Это смесь метафор и сравнений, и мне интересно, сможете ли вы идентифицировать их все.
На первый взгляд, это простая головоломка.
Но как только вы преодолеете определение первых десяти-пятнадцати идиом, становится немного сложнее. Она действительно была очень хитрой.Пожалуй, хитрая как лиса .
27 фигур речи в карикатуре Эллы Барон
К сожалению, мне не удалось найти список ответов для каждого из 27 фигур речи, представленных в карикатуре.
Возможно, Элла предпочитает разыграть свои карты, прижавшись к груди и оставить небольшую загадку, держа туза в рукаве .
Мне удалось опознать двадцать или около того по картинке, но потом я столкнулся с проблемой.Может быть, вы справитесь лучше меня и найдете все двадцать семь оборотов речи.
Но я не хочу давать вам отвлекающий маневр или проболтаться .
Так что я оставлю вас с этим. Я уверен, что это будет , проще простого .
Вы нашли все 27 фигур речи?
Если вам удастся найти пять или около того, которые я пропустил, дайте мне знать, добавив свой комментарий, чтобы избавить меня от страданий.
Не струсить !
Но сделай это быстро, пока я не сдох . Вы знаете, как быстро время летит .
Да, я знаю, что это сложная задача. Но что ж, вы не можете приготовить омлет, не разбив яйцо , не так ли?
В любом случае, я дал вам более чем достаточно подсказок, чтобы помочь вам решить головоломку на полпути. Теперь дело за вами.
Но готовы ли вы найти все 27 примеров на картинке?
Обновление этой статьи
Большое спасибо Ким, которая оставила комментарий к этой статье.Она добавила эту ссылку к ответу Эллы Бэррон в Твиттере.
В своем посте Элла перечисляет все 27 фигур речевых ответов.
Однако Элла добавляет интересное дополнение.
В ее мультфильме может быть до 49 фигур речевых выражений. Теперь, это действительно дразнить.
Но давайте избавим вас от страданий.
27 Фигуры речи ответы
Официальные ответы Эллы Бэррон
1.В двух словах
2. Кусочек пирога
3. Вишенка на торте
4. Лысый как лысуха
5. Болтающийся
6. Неподвижная верхняя губа
7. Родился с серебряной ложкой во рту
8. Ушной червь
9. Держи карты прижатыми к груди
10. Джокер в колоде
11. Туз в рукаве
12. Сердечко в рукаве
13. На блюдечке с голубой каемочкой
14. Проболтайся
15. Большой сыр
16. Красная селедка
17. Свяжите себя узами брака
18. Сложите все яйца в одну корзину
19.Ходить по яичной скорлупе
20. Тень себя прежней
21. Нет места, чтобы качать кошку
22.У кошки есть твой язык
23. Пнуть ведро
24. Подтянуть носки
25. Холодные ноги
26. От из грязи в князи
27. Время летитДругие возможные ответы
1. Взял кота за хвост
2. Ударил гвоздем по голове
3. Открутился винт
4. Рыба из воды
5. Галстук узел
6. Птичий мозг
7. Вишня сверху
8. Мел и сыр
9.Сбей носки
10. Поставь лучшую ногу вперед
11. Крепкий орешек
12. Рыба в воде
13. Банка червей
14. Большой сыр
15. Лучшей ногой вперед
16. Следуй твой нос
17. Бледный как призрак
18. Вытяни шею
19. Подними бровь
20. Дырок больше, чем в швейцарском сыре
21. Вид с высоты птичьего полета
22. Остался в лохмотьях
23. Лучшей ногой впередВот вам еще одна словесная головоломка: 18 странных слов для обычных предметов
Правильно формулируйте фигурные выражения
Если вы писатель, вы все время используете устойчивые выражения.
Тем не менее, вы должны быть осторожны, всегда проверяя свое использование и точность. Нет ничего хуже, чем ошибиться в фиксированном выражении.
В настоящее время все мы пользуемся онлайн-грамматикой и проверкой орфографии. Эти приложения чрезвычайно полезны и теперь являются важными инструментами для аккуратного письма, особенно для новых писателей.
Но эти инструменты редко найдут ошибку в использовании фраз. Например, твердый как кирпич, как храбрый как тигр, и смеется как обезьяна.
Только ваши знания могут сказать вам, какими они должны быть. Правильные выражения: твердый как скала , храбрый как лев , и смеется как гиена .
То же самое относится к акронимам и аббревиатурам. Использование средства проверки грамматики вряд ли поможет вам отличить am от am или SCABA , когда вы имеете в виду SCUBA .

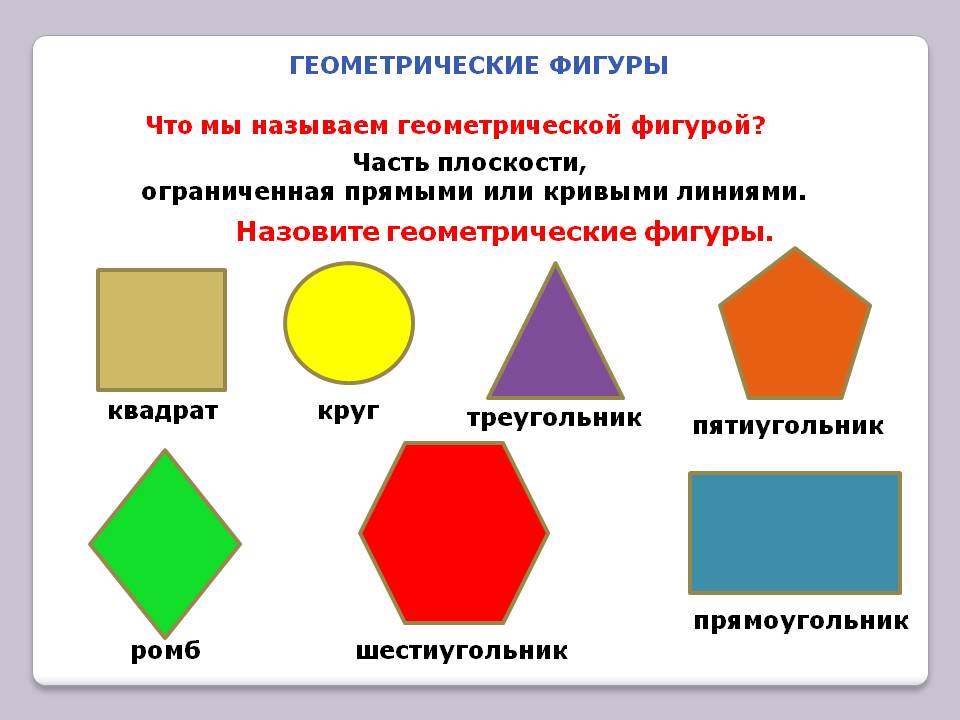 То есть, если вы надеваете объёмный верх, то автоматически становитесь перевернутым треугольником, если объёмный низ, то грушей. Хорошо это или плохо, зависит от ваших вкусов и целей.
То есть, если вы надеваете объёмный верх, то автоматически становитесь перевернутым треугольником, если объёмный низ, то грушей. Хорошо это или плохо, зависит от ваших вкусов и целей.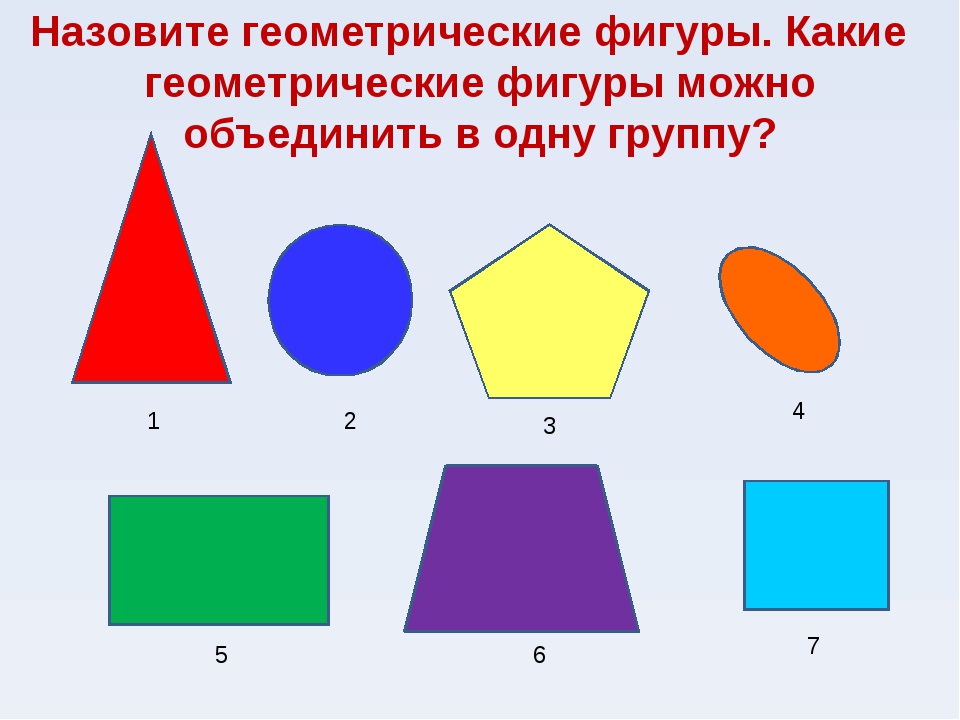
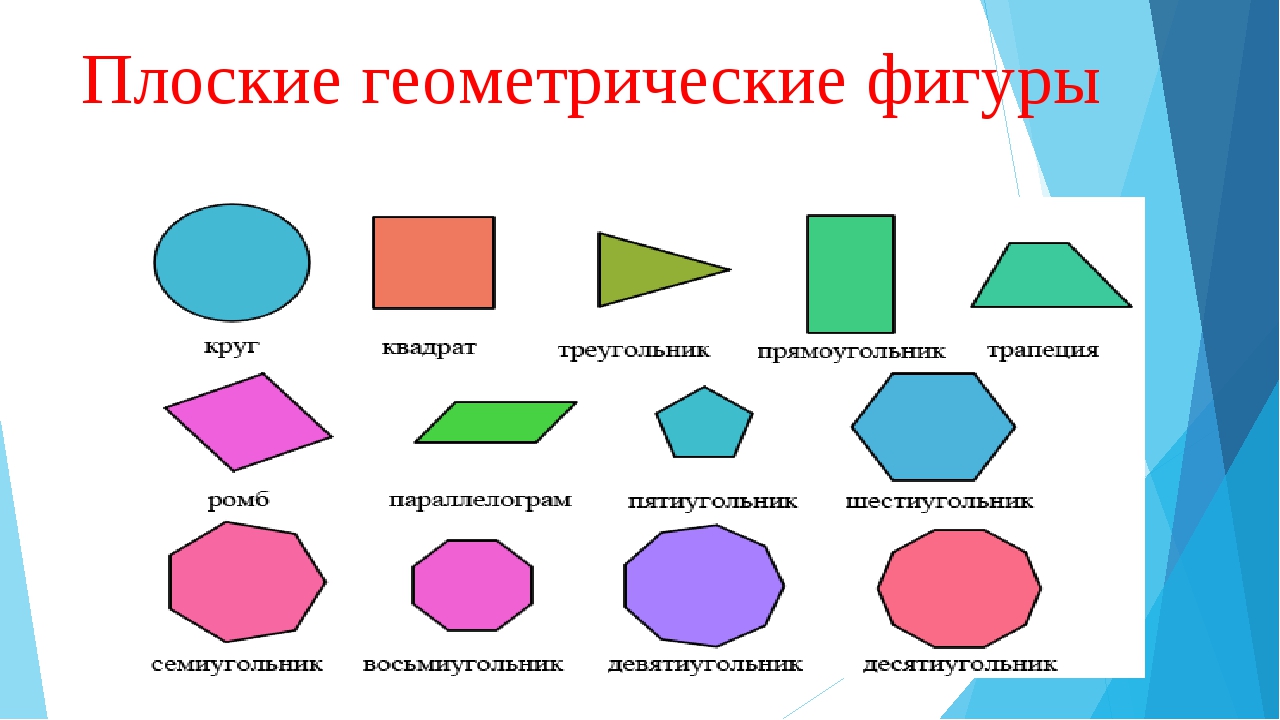

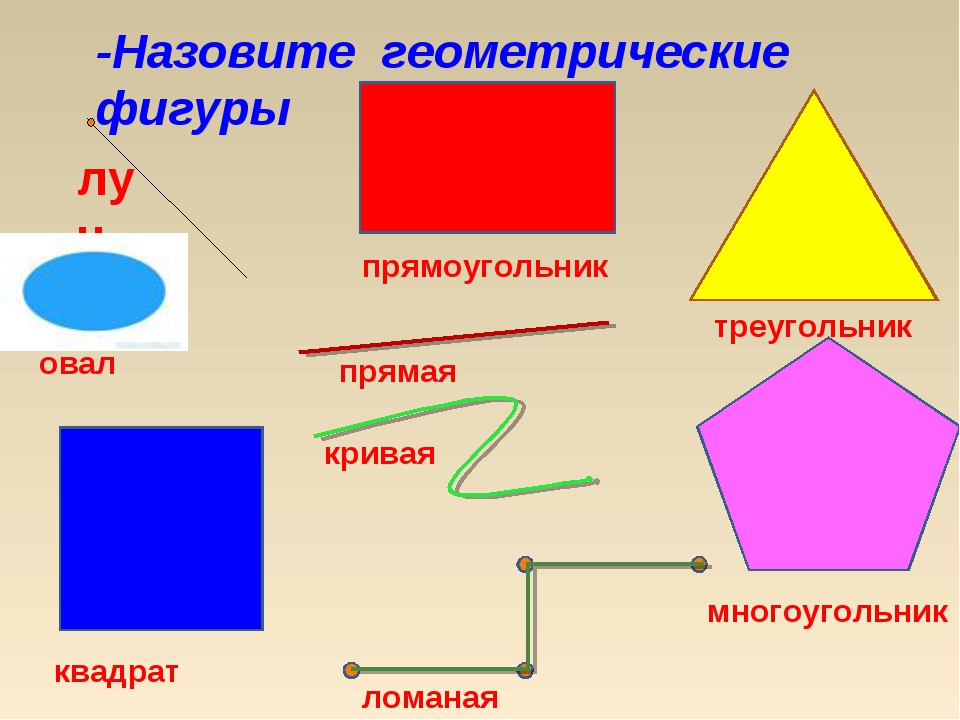
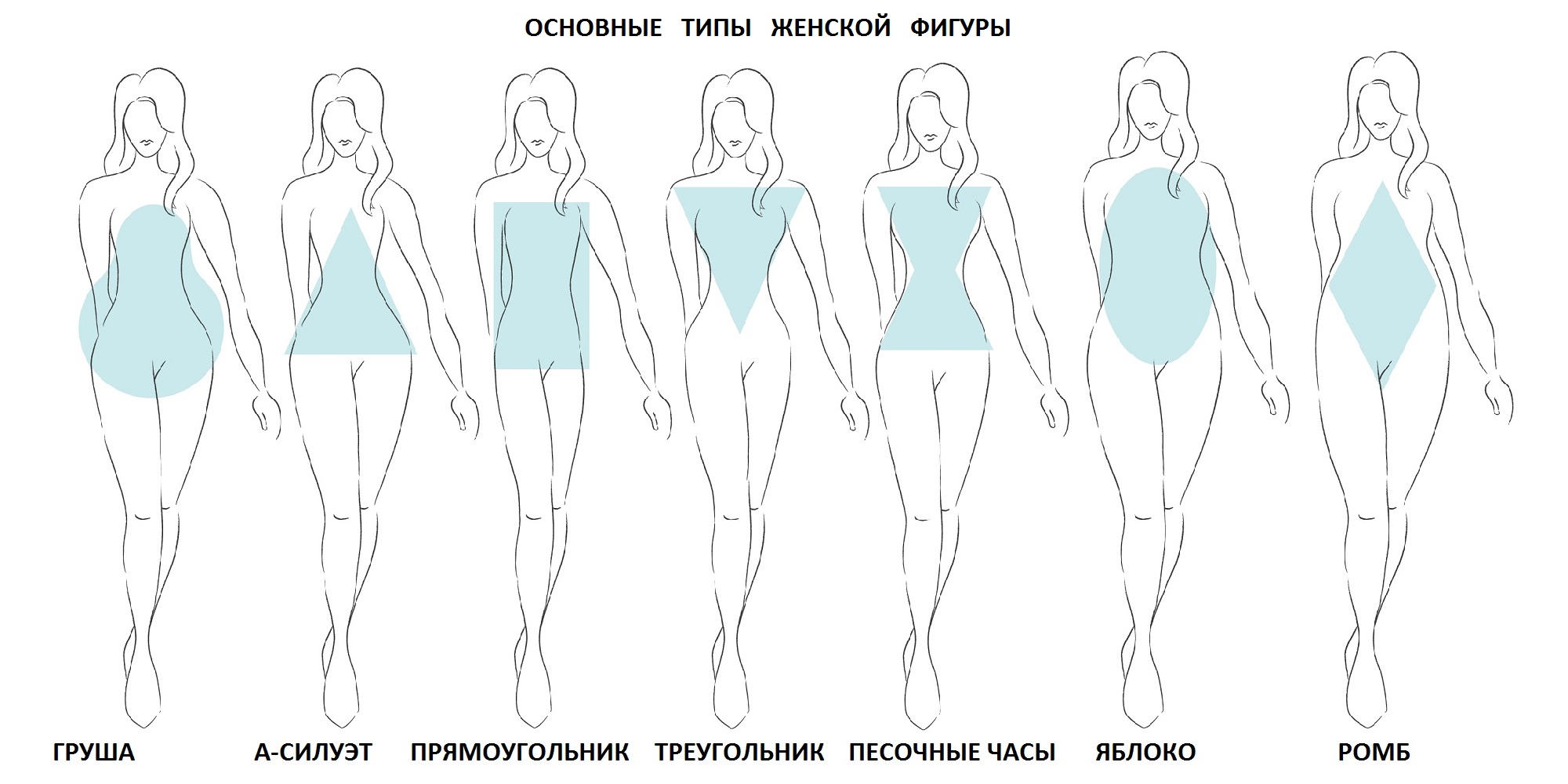 При наведении указателя мыши на значок появляется название набора.
При наведении указателя мыши на значок появляется название набора. Одежда по типу фигуры трапеция — полуприлегающая и табу на обтягивающую.
Одежда по типу фигуры трапеция — полуприлегающая и табу на обтягивающую.
 Путешествие по такой ленте Мебиуса всегда будет бесконечным, оно приведет к начальной точке пути, только в зеркальном отображении.
Путешествие по такой ленте Мебиуса всегда будет бесконечным, оно приведет к начальной точке пути, только в зеркальном отображении.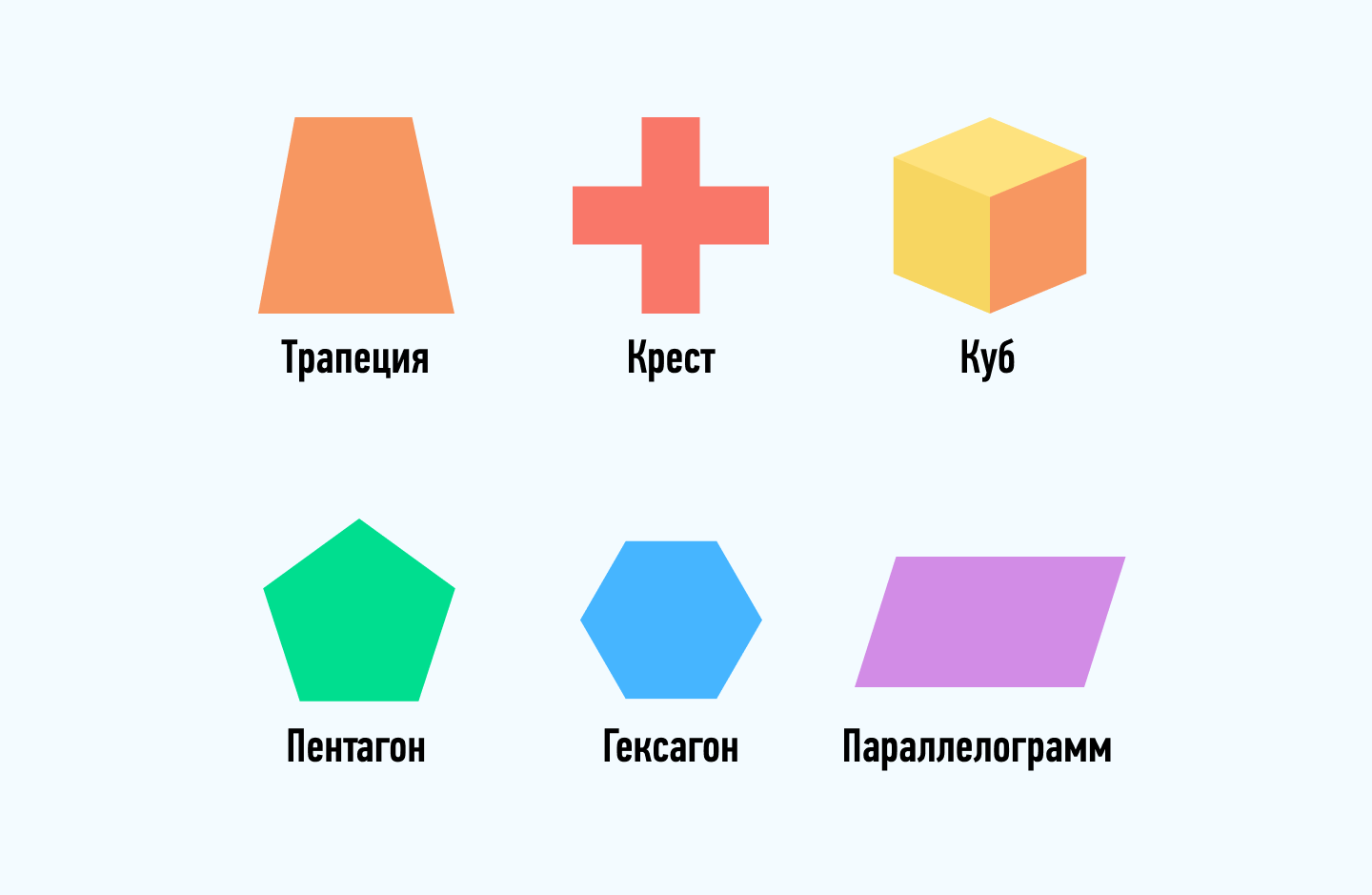
 Работа «Черный квадрат» всегда была мистической и загадочной. Геометрическая фигура на белом полотне восхищает и поражает одновременно.
Работа «Черный квадрат» всегда была мистической и загадочной. Геометрическая фигура на белом полотне восхищает и поражает одновременно. Вот несколько распространенных примеров разговорных фигур речи:
Вот несколько распространенных примеров разговорных фигур речи: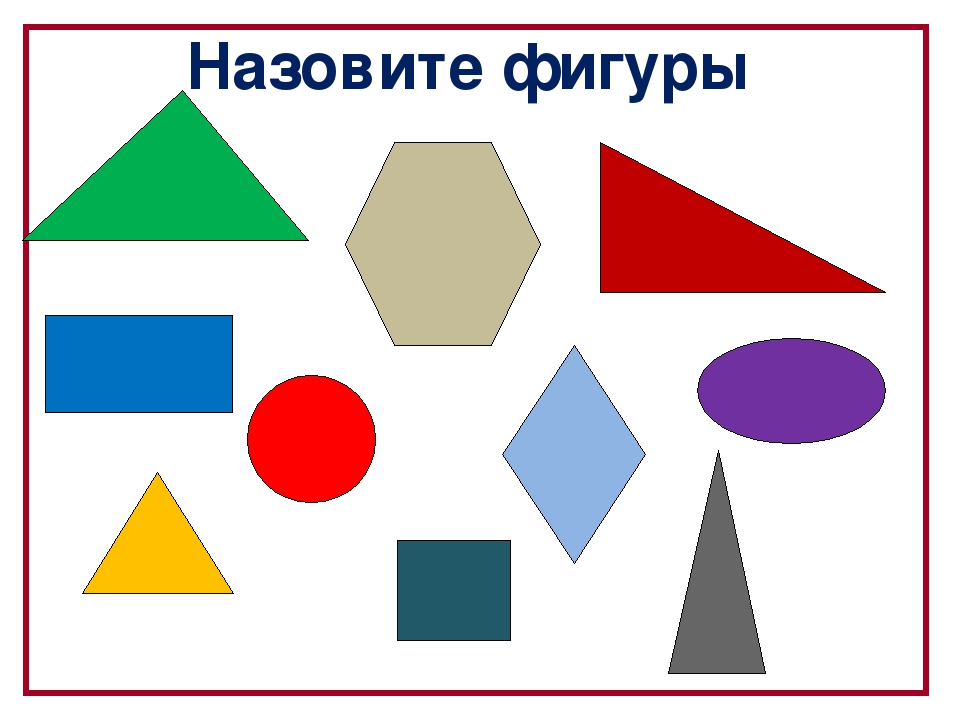
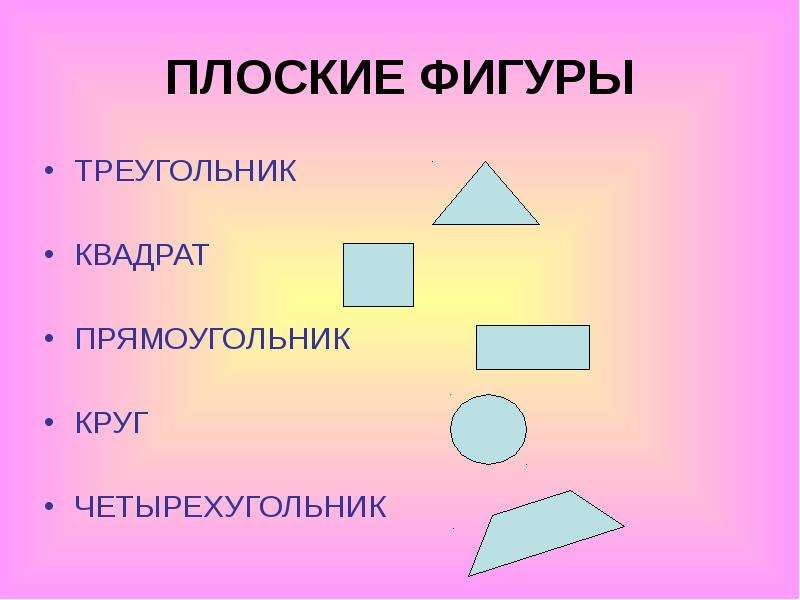
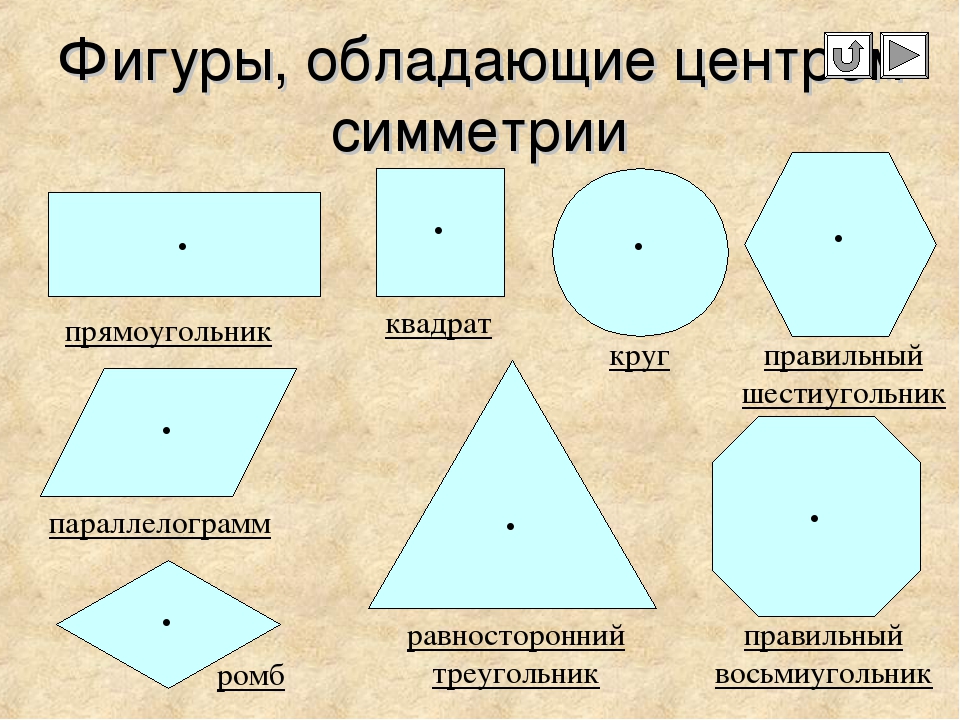
 В письменной речи, когда фигуры речи используются эффективно, эти приемы улучшают способность писателя к описанию и выражению, так что читатели лучше понимают, что передается.
В письменной речи, когда фигуры речи используются эффективно, эти приемы улучшают способность писателя к описанию и выражению, так что читатели лучше понимают, что передается.
 Вот несколько примеров фигур речи в известных литературных произведениях:
Вот несколько примеров фигур речи в известных литературных произведениях:
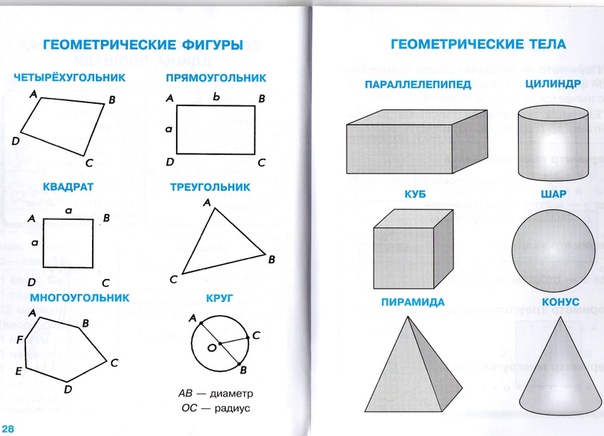 Конечно, Брэдбери утверждает, что книга — это заряженное ружье только как средство переносного, а не буквального значения.Эта метафора особенно сильна, потому что сравнение маловероятно; книги вообще не считаются опасным оружием. Тем не менее, сравнение имеет определенный уровень логики в контексте истории, в которой стремление к знаниям используется как оружие и криминализовано.
Конечно, Брэдбери утверждает, что книга — это заряженное ружье только как средство переносного, а не буквального значения.Эта метафора особенно сильна, потому что сравнение маловероятно; книги вообще не считаются опасным оружием. Тем не менее, сравнение имеет определенный уровень логики в контексте истории, в которой стремление к знаниям используется как оружие и криминализовано. Однако, если бы вы их измерили, вы бы обнаружили, что соответствующие стороны обоих треугольников совершенно одинаковы. На самом деле второй треугольник такой же, как и первый; его просто повернули.Значит, эти фигуры равны.
Однако, если бы вы их измерили, вы бы обнаружили, что соответствующие стороны обоих треугольников совершенно одинаковы. На самом деле второй треугольник такой же, как и первый; его просто повернули.Значит, эти фигуры равны.
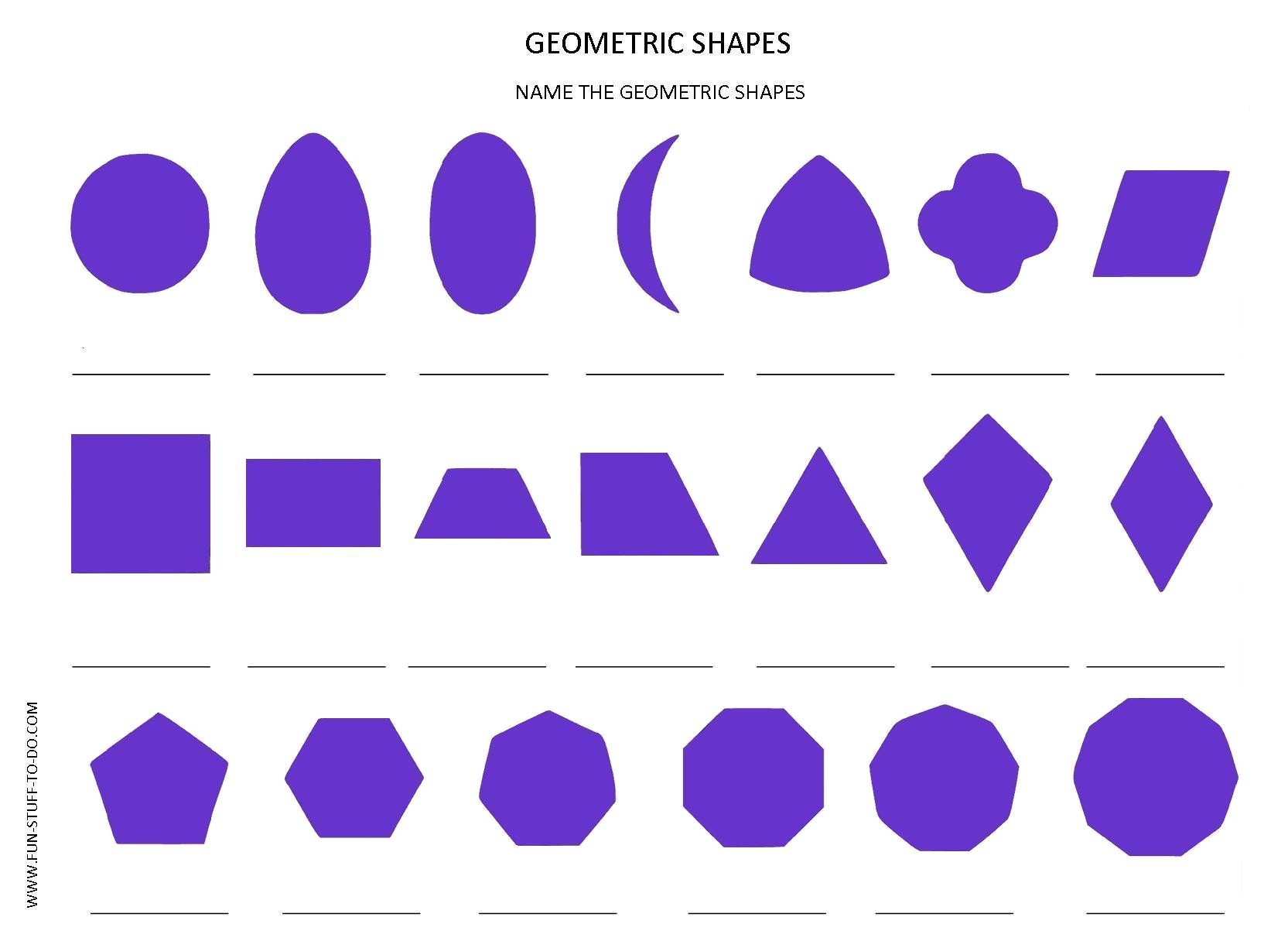
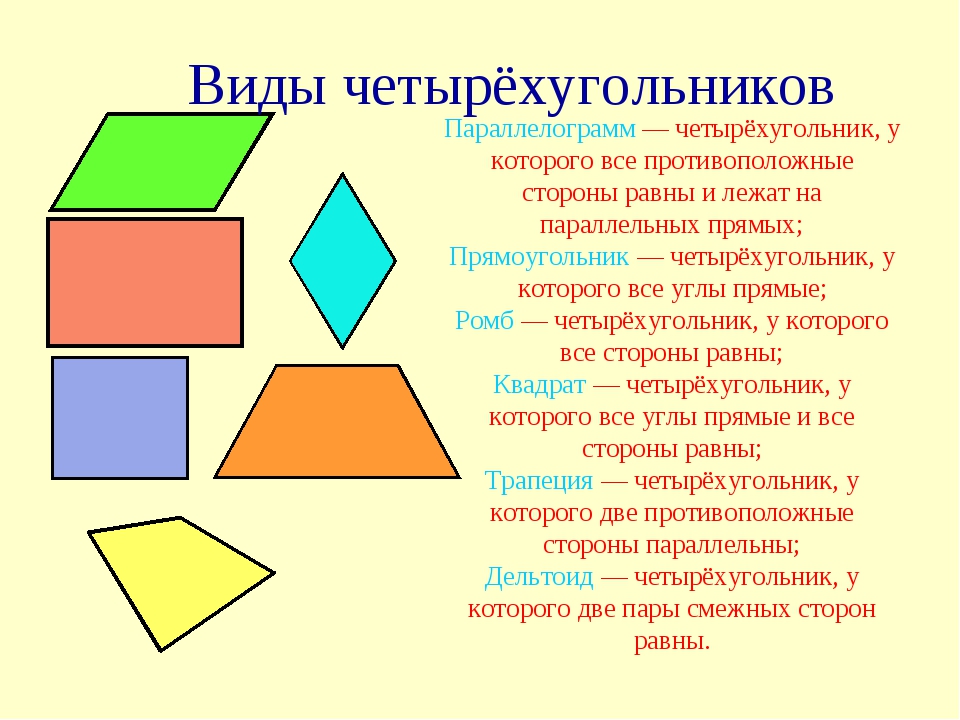 0 Смысловые числа: 2, 11
0 Смысловые числа: 2, 11 


 99
99 99
99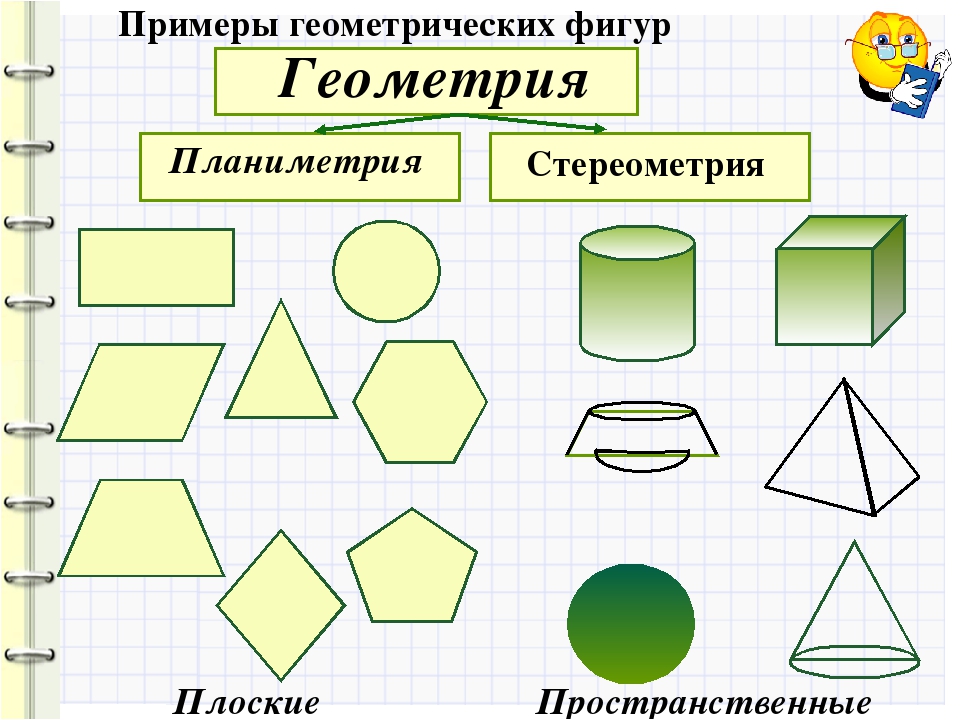 99
99 Наряд: Peter Tork .
Наряд: Peter Tork .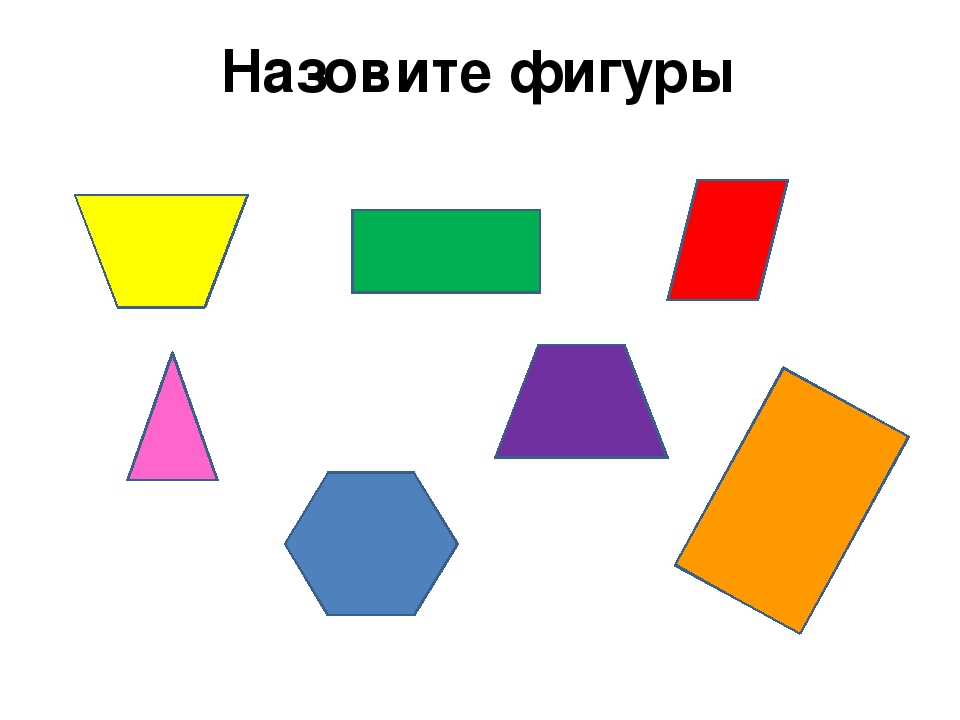 99
99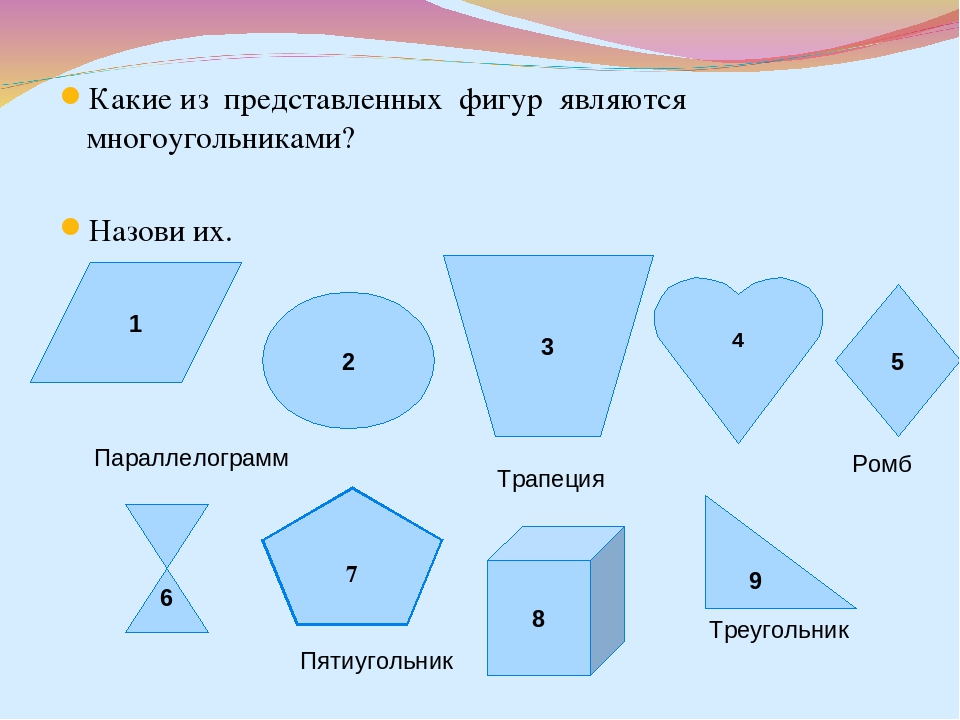 Кеннеди, коллекционная
Кеннеди, коллекционная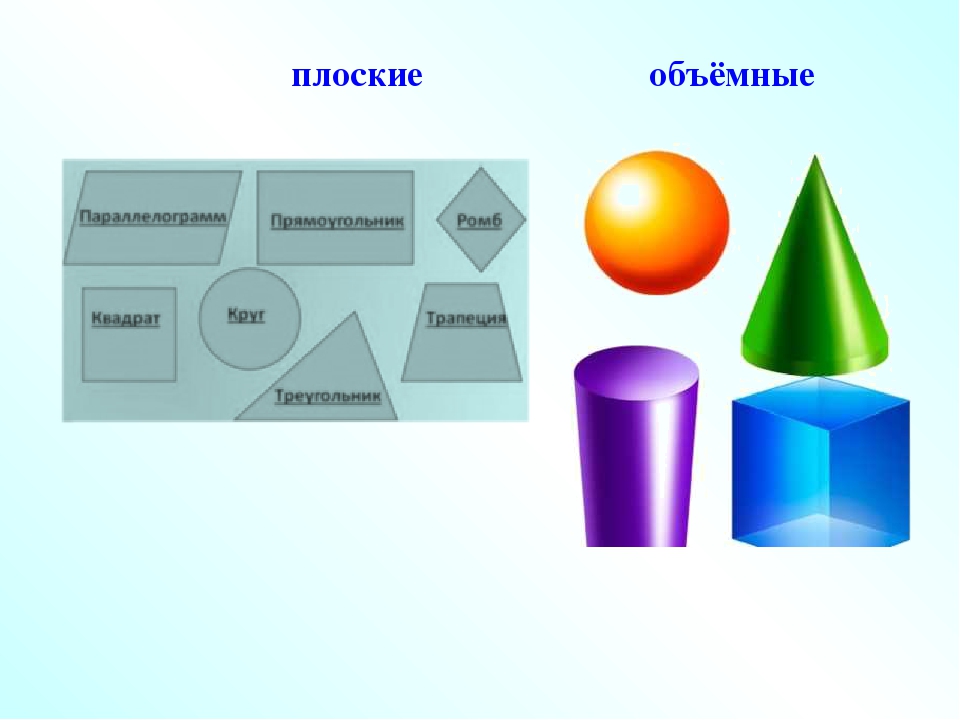 и красноречивая речь.
и красноречивая речь.
 Использование одного для описания другого.
Использование одного для описания другого.
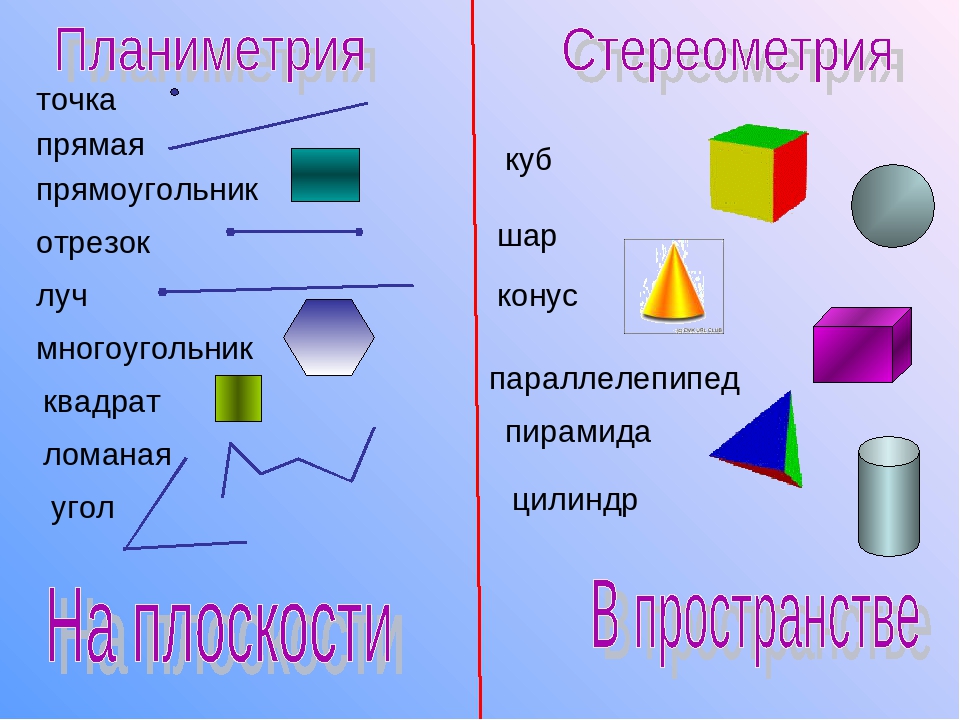


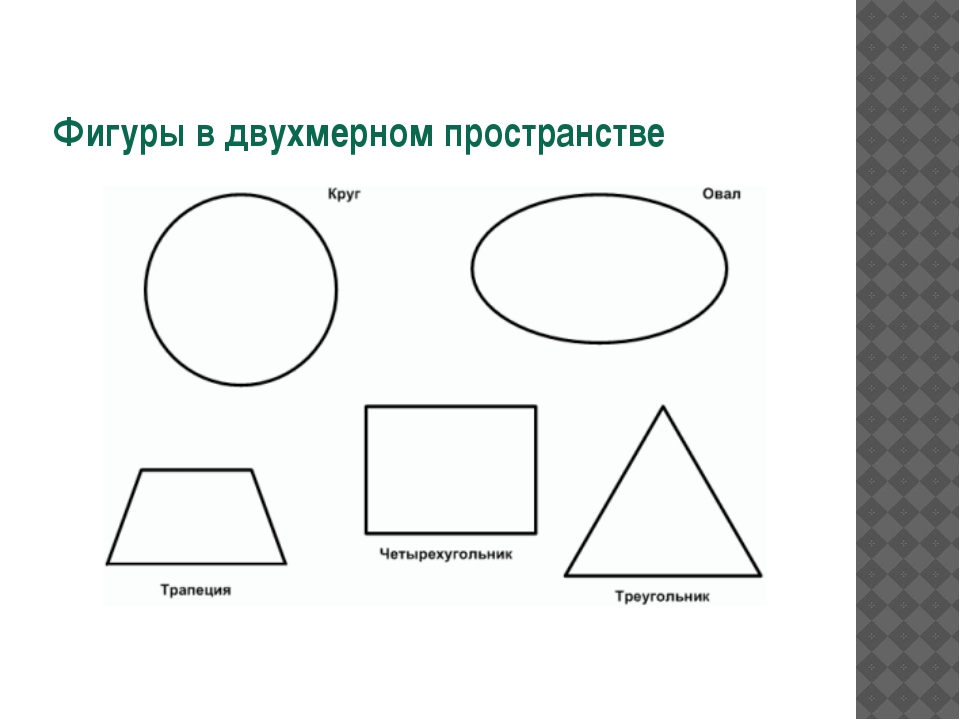


 Точно так же легенды или подписи предоставляют описательную информацию о рисунках или таблицах.
Точно так же легенды или подписи предоставляют описательную информацию о рисунках или таблицах. д.) при описании больших объемов данных.
д.) при описании больших объемов данных.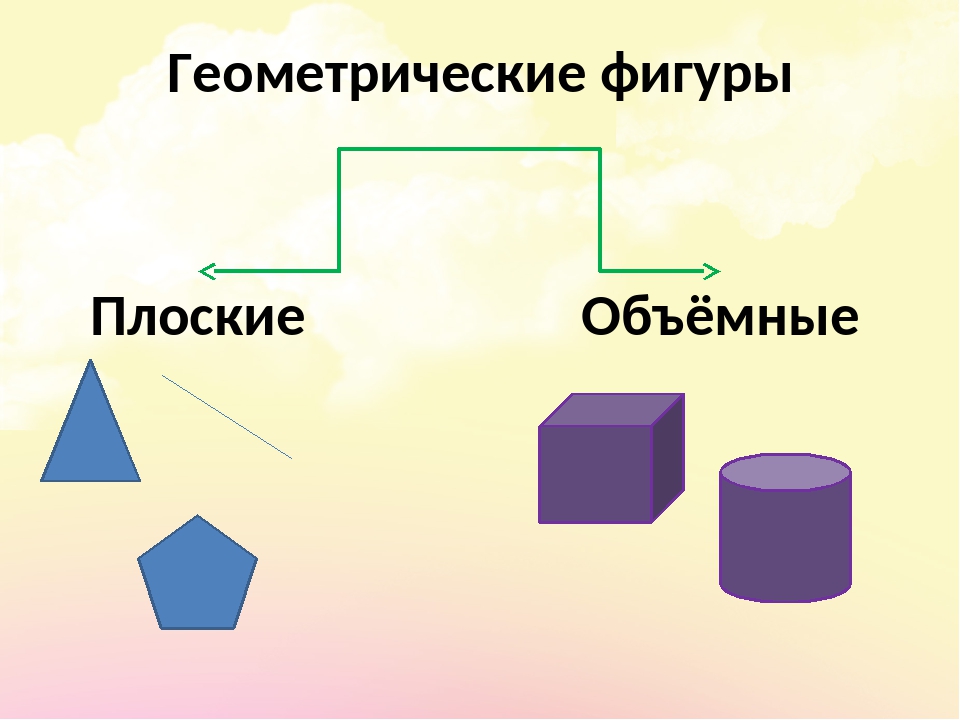
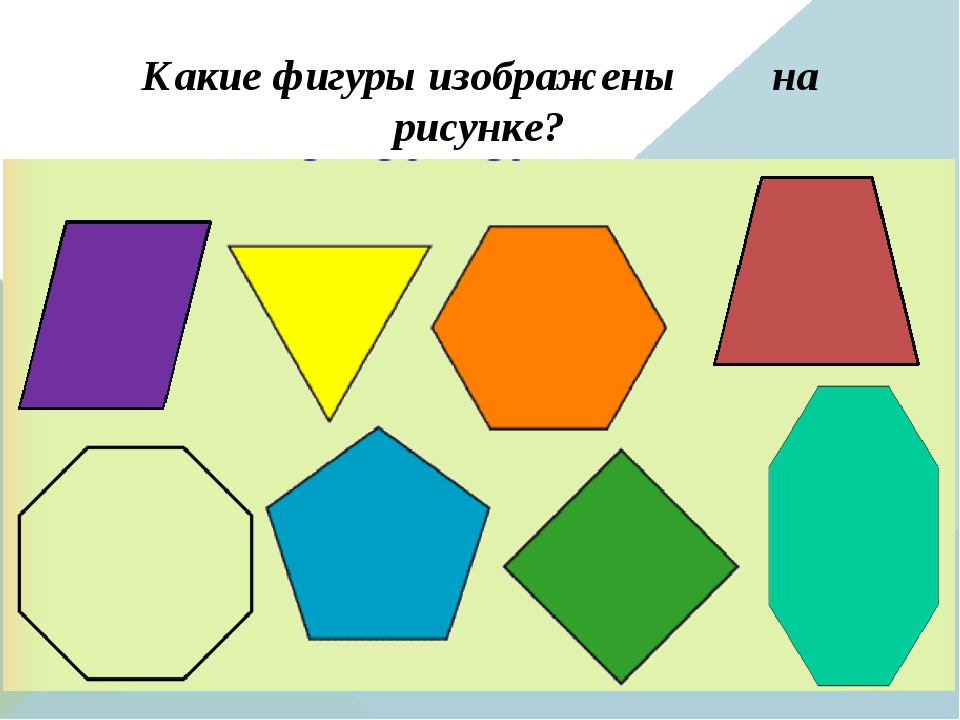
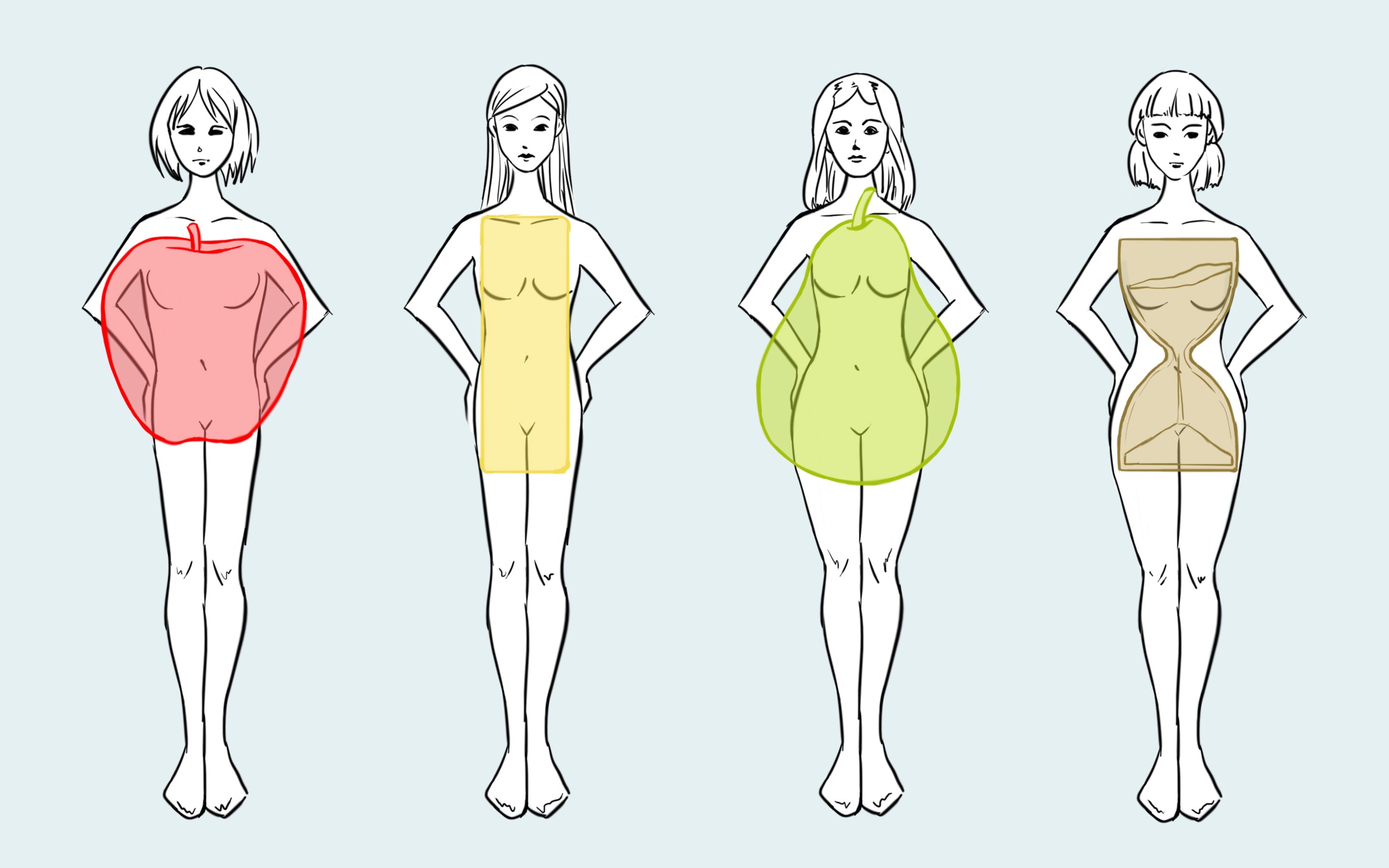
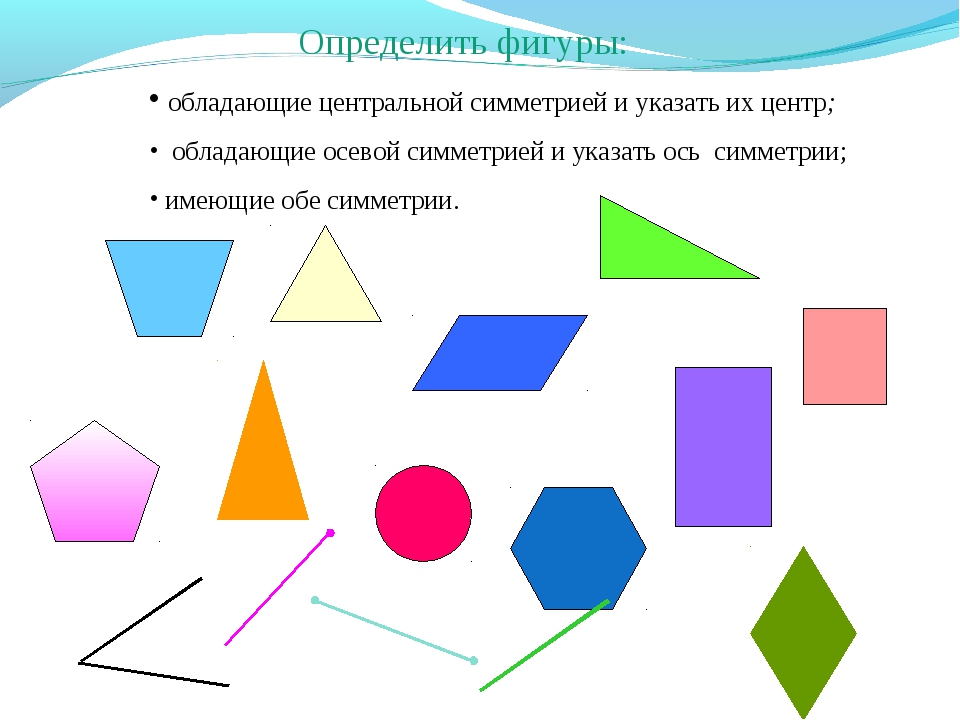
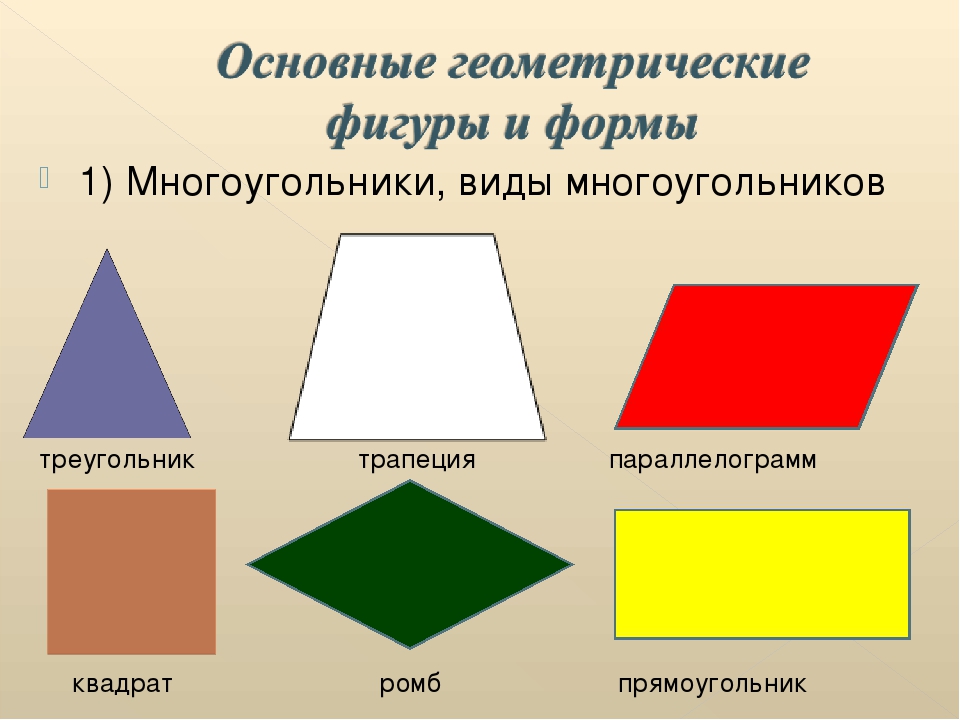
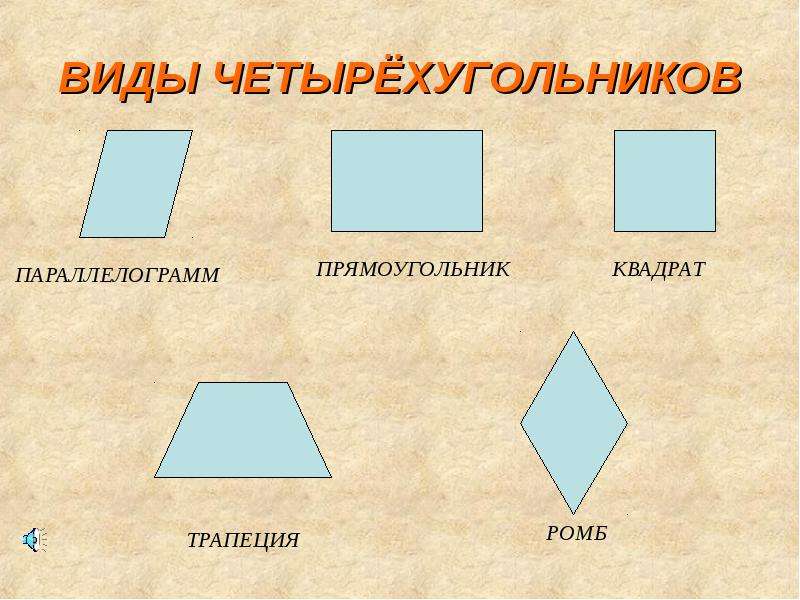

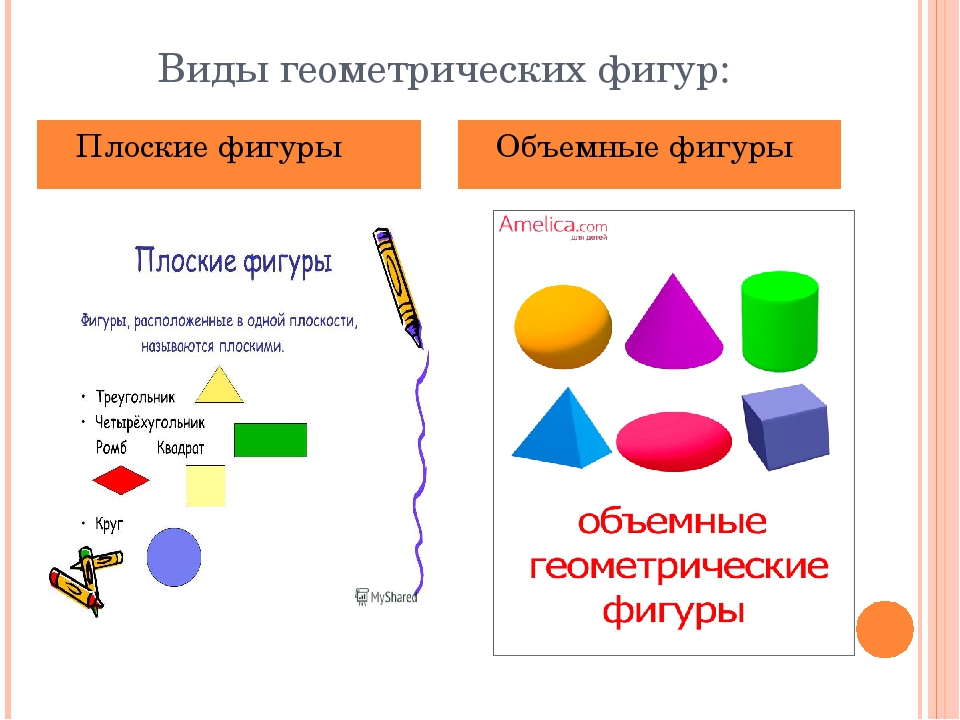 Например, Я занят как пчела, и он мертв как дверной гвоздь или додо .
Например, Я занят как пчела, и он мертв как дверной гвоздь или додо .  Это смесь метафор и сравнений, и мне интересно, сможете ли вы идентифицировать их все.
Это смесь метафор и сравнений, и мне интересно, сможете ли вы идентифицировать их все.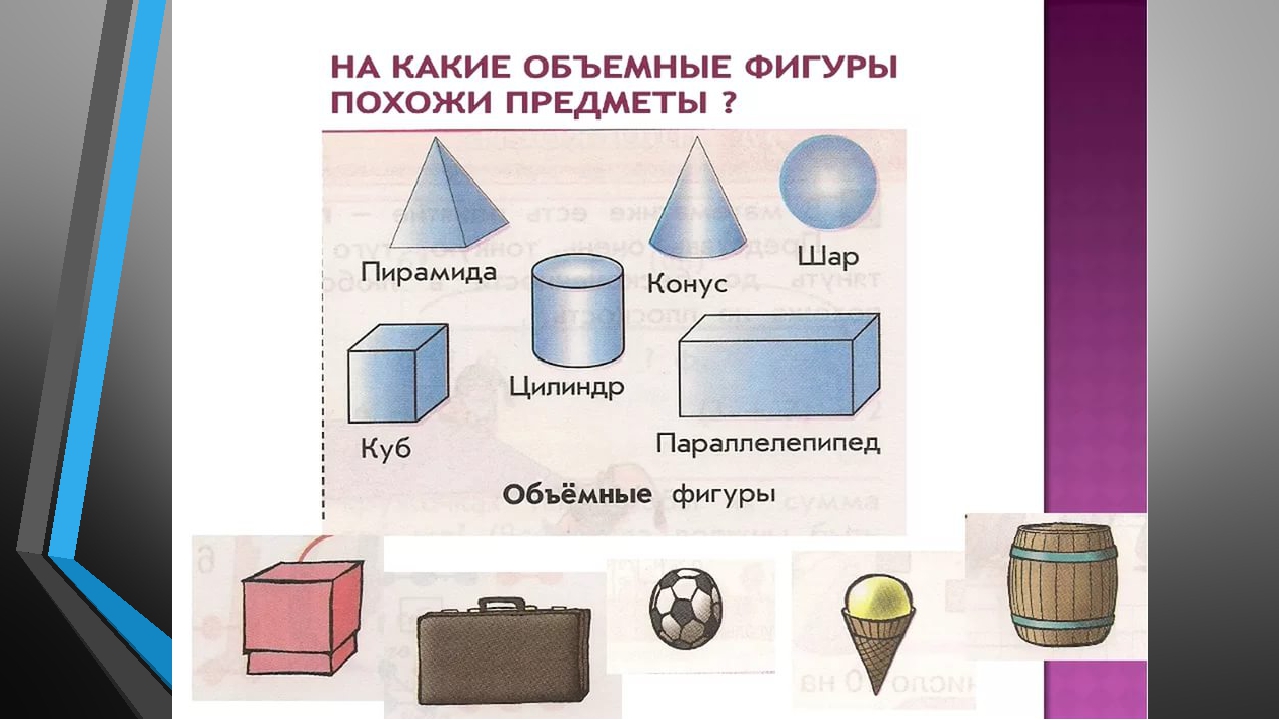 Так что я оставлю вас с этим. Я уверен, что это будет , проще простого .
Так что я оставлю вас с этим. Я уверен, что это будет , проще простого .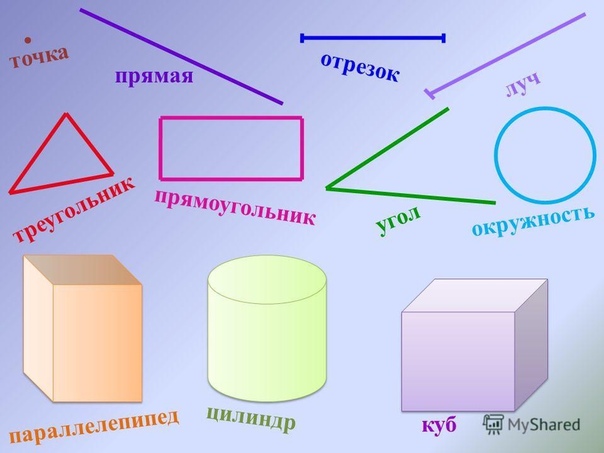 В своем посте Элла перечисляет все 27 фигур речевых ответов.
В своем посте Элла перечисляет все 27 фигур речевых ответов. 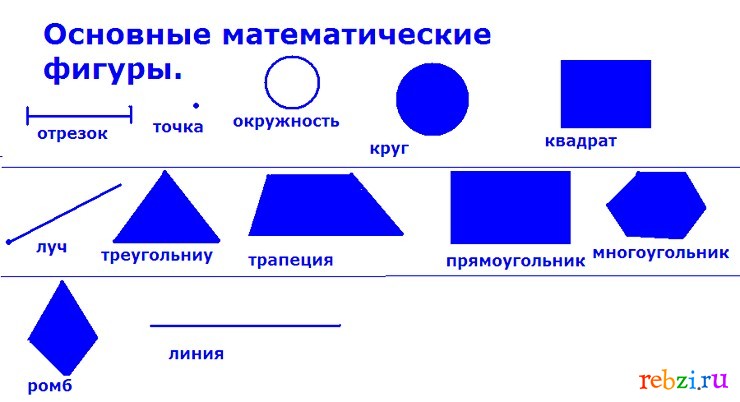 У кошки есть твой язык
У кошки есть твой язык