Вес и невесомость | Физика
1. Вес тела, движущегося с ускорением
В § 12 мы доказали, что вес покоящегося тела равен действующей на это тело силе тяжести. Рассмотрим теперь вес тела, движущегося с ускорением. Это ускорение телу сообщает равнодействующая силы тяжести и силы, действующей со стороны опоры (или подвеса).
Поэтому, говоря далее об ускорении тела, мы должны понимать, что оно равно ускорению опоры (или подвеса).
Ускорение тела направлено вверх. Докажем, что в таком случае модуль веса тела
P = m(g + a), (1)
где m – масса тела, a – модуль ускорения тела.
Пусть тело массой m лежит на опоре, движущейся с ускорением , направленным вверх (рис. 16.1, а).
Тело давит на опору своим весом , а опора действует на груз с силой нормальной реакции ). По третьему закону Ньютона
= –. (2)
Отсюда следует, что
P = N. (3)
На тело действуют сила тяжести mg_vec и сила нормальной реакции (рис.
Следовательно, согласно второму закону Ньютона
+ m = m.
Запишем эту формулу в проекциях на направленную вверх ось x:
N – mg = ma.
Отсюда
N = m(g + a) (4)
Из формул (3) и (4) следует, что
P = m(g + a).
Доказательство завершено: мы получили формулу (1).
Обратите внимание: если ускорение тела направлено вверх, вес груза больше действующей на него силы тяжести.
Когда вес тела больше силы тяжести, говорят, что оно испытывает перегрузку. Здоровый человек без вреда выдерживает кратковременные трехкратные перегрузки, то есть увеличение веса в три раза.
Космонавтам при старте и посадке космического корабля приходится выдерживать многократные перегрузки. Чтобы это не нанесло ущерба здоровью космонавтов, их тренируют с помощью специального аппарата – центрифуги (см. § 8).
Ускорение направлено вниз. Будем считать,что ускорение тела не превышает по модулю ускорения свободного падения.
? 1. Докажите, что в этом случае
P = m(g – a). (5)
Итак, если ускорение тела направлено вниз, то вес тела меньше действующей на него силы тяжести.
Из формулы (5) следует, что при a = g, то есть когда тело движется с ускорением свободного падения, вес тела равен нулю. Подробнее мы рассмотрим это в пункте «Невесомость».
Обратите внимание: в формулы (1) и (5) для веса тела, движущегося с ускорением, не входит скорость тела. Это означает, что вес тела не зависит от модуля и направления скорости тела.
Например, если ускорение тела в некоторый момент направлено вверх, то вес будет больше действующей на это тело силы тяжести независимо от того, куда направлена скорость тела: вверх, вниз, горизонтально или под углом к горизонту!
? 2. Через 2 с после начала движения с постоянным ускорением скорость лифта стала равной 6 м/с. В лифте на весах стоит пассажир массой 60 кг. Каковы во время разгона лифта показания весов (в кг), если лифт едет вверх? вниз?
? 3. Лифт, двигавшийся со скоростью 4 м/с, начал тормозить. Во время торможения с постоянным ускорением вес находящегося в лифте человека массой 50 кг был равен 400 Н.
Лифт, двигавшийся со скоростью 4 м/с, начал тормозить. Во время торможения с постоянным ускорением вес находящегося в лифте человека массой 50 кг был равен 400 Н.
а) Куда направлено ускорение лифта?
б) Чему равно ускорение лифта?
в) Куда ехал лифт до остановки – вверх или вниз?
? 4. Подвешенный на нити длиной 1 м груз массой 0,5 кг совершает колебания в вертикальной плоскости (рис. 16.2). В нижней точке скорость груза равна 2 м/с.
а) Как направлено в нижней точке ускорение груза?
б) Чему равно ускорение груза в нижней точке?
в) Чему равна сила натяжения нити в нижней точке?
? 5. Автомобиль массой 1 т едет по выпуклому мосту, имеющему форму дуги окружности радиусом 40 м. Какой должна быть скорость автомобиля в верхней точке моста, чтобы в этой точке:
а) вес автомобиля был равен 2 кН?
б) автомобиль не давил на мост?
? 6. К пружине жесткостью 400 Н/м подвешивают груз массой 200 г, в результате чего пружина растягивается. Какова кратность перегрузки для груза в момент, когда удлинение пружины равно 2 см?
2.
 Невесомость
НевесомостьВ предыдущем пункте была получена формула для веса тела, находящегося на опоре, движущейся с ускорением а, направленным вниз:
P = m(g – a).
(Мы считаем, что модуль ускорения тела не превышает ускорения свободного падения.)
Из этой формулы следует, что, когда ускорение опоры приближается к ускорению свободного падения у, вес тела стремится к нулю.
При a = g тело совсем перестает давить на опору. В этот момент вес тела становится ровным нулю. Такое состояние называют невесомостью.
Итак, тело находится в состоянии невесомости, когда оно под действием силы тяжести движется с ускорением свободного падения . При этом оно не давит на опору и не растягивает подвес, поэтому их можно вообще убрать.
Однако находящееся в состоянии невесомости тело не обязательно должно падать вниз! Вспомним, что ускорение брошенного произвольным образом тела во время всего полета равно ускорению свободного падения (если можно пренебречь сопротивлением воздуха). Следовательно, брошенное тело находится в состоянии невесомости во время всего полета.
Следовательно, брошенное тело находится в состоянии невесомости во время всего полета.
? 7. Шарик брошен вертикально вверх. В какие моменты он находится в состоянии невесомости: при подъеме, в верхней точке траектории или когда он падает вниз?
Чтобы испытать кратковременное состояние невесомости, достаточно просто подпрыгнуть (рис. 16.З).
Длительное состояние невесомости испытывают космонавты при выключенных двигателях космического корабля. При этом как корабль, так и космонавты находятся под действием только силы тяжести, то есть движутся с ускорением свободного падения.
Поставим опыт
Нальем воду в пластиковую бутылку с отверстием в дне. Вода будет вытекать из отверстия. Но если бросить бутылку (в любом направлении), то во время полета бутылки вода из нее не выливается! Дело в том, что бутылка н вода в ней находятся в невесомости: вода не давит на дно бутылки и поэтому не выливается.
? 8. Шарик скатывается по «мертвой петле» радиусом 20 см (рис. 16.4), не отрываясь от нее. Чему равна скорость шарика в верхней точке окружности, если в этой точке он находится в состоянии невесомости?
16.4), не отрываясь от нее. Чему равна скорость шарика в верхней точке окружности, если в этой точке он находится в состоянии невесомости?
Подсказка. Если шарик находится в состоянии невесомости, центростремительное ускорение ему сообщает только сила тяжести.
Дополнительные вопросы и задания
9. К пружине жесткостью k подвешивают груз массой m и отпускают без толчка. Чему равен вес груза в тот момент когда:
б) удлинение пружины равно x?
10. На тележке укреплен штатив, на котором на нити подвешен груз (рис. 16.5). Какой угол α с вертикалью составляет нить, когда тележка движется с ускорением a = 5 м/с2?
Подсказка. Ускорение грузу сообщает равнодействующая силы тяжести m и силы натяжения нити .
Сила тяжести — в чем измеряется? Чему равна?
Сила: что это за величина
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.
В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.
Сила — это физическая векторная величина, которую воздействует на данное тело со стороны других тел.
Она измеряется в Ньютонах — это единица измерения названа в честь Исаака Ньютона.
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.
Сила тяготения
В 1682 году Исаак Ньютон открыл Закон Всемирного тяготения. Он звучит так: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними.
Формула силы тяготения согласно этому закону выглядит так:
Закон Всемирного тяготения F = GMm/R2 F — сила тяготения [Н] M — масса первого тела (часто планеты) [кг] m — масса второго тела [кг] R — расстояние между телами [м] G — гравитационная постоянная G = 6.67 × 10-11 м3 кг-1 с-2 |
Когда мы встаем на весы, стрелка отклоняется. Это происходит потому, что масса Земли очень большая, и сила тяготения буквально придавливает нас к поверхности. На более легкой Луне человек весит меньше в шесть раз.
Закон всемирного тяготения используют, чтобы вычислить силы взаимодействия между телами любой формы, если размеры тел значительно меньше расстояния между ними.
Если мы возьмем два шара, то для них можно использовать этот закон вне зависимости от расстояния между ними. За расстояние R между телами в этом случае принимается расстояние между центрами шаров.
Приливы и отливы существуют благодаря Закону Всемирного тяготения. В этом видео я рассказываю, что общего у приливов и прыщей
Несколько лет назад ученые открыли такое явление, как гравитационные волны — но это не тоже самое, что гравитация:
Источник: YouTube-канал «Это работает»
Сила тяжести
Сила тяжести — сила, с которой Земля притягивает все тела.
F = mg F — сила тяжести [Н] m — масса тела [кг] g — ускорение свободного падения [м/с2] На планете Земля g = 9,8 м/с2 |
На первый взгляд сила тяжести очень похожа на вес тела. Действительно, в состоянии покоя на поверхности Земли формулы силы тяжести и веса идентичны. Но разница все-таки есть, давайте разбираться.
Действительно, в состоянии покоя на поверхности Земли формулы силы тяжести и веса идентичны. Но разница все-таки есть, давайте разбираться.
Эта формула и правда аналогична силе тяжести. Вес тела в состоянии покоя численно равен массе тела, разница состоит лишь в точке приложения силы.
Сила тяжести — это сила, с которой Земля действует на тело, а вес — сила, с которой тело действует на опору. Это значит, что у них будут разные точки приложения: у силы тяжести к центру масс тела, а у веса — к опоре.
Также, важно понимать, что сила тяжести зависит исключительно от массы и планеты, на которой тело находится. Вес зависит также от ускорения, с которым движутся тело или опора.
Например, в лифте вес тела зависит от того, куда и с каким ускорением движется тело. А силе тяжести все равно, куда и что движется — она не зависит от внешних факторов.
На второй взгляд сила тяжести очень похожа на силу тяготения. В обоих случаях мы имеем дело с притяжением — значит можем сказать, что это одно и то же. Практически.
В обоих случаях мы имеем дело с притяжением — значит можем сказать, что это одно и то же. Практически.
Мы можем сказать, что это одно и то же, если речь идет о Земле и каком-то предмете, который к этой планете притягивается. Тогда мы можем даже приравнять эти силы и выразить формулу для ускорения свободного падения.
F = mg
F = GMm/R2
Приравниваем правые части:
mg = GMm/R2
Делим на массу левую и правую части:
g = GM/R2
Это и будет формула ускорения свободного падения. Ускорение свободного падения для каждой планеты уникально, эта формула нужна.
Формула для ускорения свободного падения g = GM/R2 F — сила тяготения [Н] M — масса планеты [кг] R — расстояние между телами [м] G — гравитационная постоянная G = 6. |
А теперь задачка
Определить силу тяжести, действующую на тело массой 80 кг.
Решение:
Не смотря на кажущуюся простоту, тут есть над чем подумать.Вроде бы просто нужно взять формулу F = mg, подставить числа и дело в шляпе.
Да, но есть один нюанс: в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают то же значения, что мы указывали выше: g = 9,8 м/с2.
В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с2.
И кому же верить?
Все просто: для кого решается задача, тот и главный. В экзаменах берем g = 10 , в школе при решении задач (если в условии задачи не написано что-то другое) берем g = 9,8 м/с2.
Итак, F = mg.
F = 80*10 = 800 Н
Ответ: 800 Н.
Учимся летать
В серии книг Дугласа Адамса «Автостопом по Галактике» говорится, что летать — это просто промахиваться мимо Земли. Если ты промахнулся мимо Земли и достиг первой космической скорости 7,9 км/с, то ты стал искусственным спутником Земли.
Искусственный спутник Земли — космический летательный аппарат, который вращается вокруг Земли по геоцентрической орбите. Чтобы у него так получалось, аппарат должен иметь начальную скорость, равную или большую первой космической скорости.
Кстати, есть еще вторая и третья космические скорости. Вторая космическая скорость — это скорость, которая нужна, чтобы корабль стал искусственным спутником Солнца, а третья — чтобы вылетел за пределы солнечной системы.
Подробнее о возможностях полетов и невесомости читайте в нашей статье про вес тела.
Таблица 3 / КонсультантПлюс
Определение веса сена
N участка, луга, клетки | N скирд, стогов | Результаты измерений | Вес одного кубометра, кг | Общий вес скирды, ц | |||||||
Чтобы определить объем скирды пользуются следующей формулой:
(П x 0,56) — (Ш x 0,55) x ШД,
где П — перекидка, Ш — ширина, Д — длина.
Для определения объема стогов пользуются следующей формулой:
ОБ = (0,04П — 0,012C)C2,
где ОБ — объем, П — перекидка, C — окружность.
Например, перекидка стога равна 6 м, длина окружности — 10 м, вес — 1 м3 сена — 50 кг. Объем стога составит:
ОБ = (0,04 x 6 — 0,012 x 10) x 100 = (0,24 — 0,12) x 100 = 12 м3.
Зная вес 1 м3 сена определяется вес всего стога (12 x 50) = 600 кг, или 6 ц.
Расчеты комиссии по определению объемов каждого стога или скирды и определения веса сена служат основанием для составления акта приема грубых и сочных кормов (Форма N СП-17). Акт на приемку грубых и сочных кормов составляется отдельно на каждый вид заготовленного корма (сено, силос, солома, корнеплоды и др.) в двух экземплярах. Первый экземпляр акта передается в бухгалтерию организации и служит основанием для оприходования кормов, второй со схемой расположения стогов, скирд и т.д. передается фуражиру или другому лицу, принявшему корма (зав. фермой). В акте указывают состав комиссии, место расположения кормов, площадь, с которой собраны корма, номера скирд и стогов, размеры каждой в отдельности скирды, объем в кубических метрах, вес 1 м3 и вес всей скирды (стога) в центнерах. К акту прилагается схема расположения стогов, скирд, башен, траншей и буртов.
К акту прилагается схема расположения стогов, скирд, башен, траншей и буртов.Акт подписывают члены комиссии по приему кормов, бригадир (ответственный за работы) и материально ответственное лицо. Кроме того, он рассматривается и утверждается руководителем организации.
Принятые комиссией скирды и стога сена закрепляют за фермами, бригадами или отдельными откормочными пунктами и передают под ответственность материально ответственных лиц. При этом составляется опись кормов, в которой указывается вид кормов, их нахождение, количество в натуре, количество кормо-единиц и переваримого протеина (по данным вет-лаборатории), в конце описи роспись заведующего фермой или бригадира (таблица 4).
Подписи членов комиссии:
Открыть полный текст документа
Расчет веса металла — как вычислить с помощью калькулятора?
Очень часто, имея в наличии только габариты проката, необходимо выполнить расчет удельного веса листового металла по размерам, и тогда возникает нужда в простых способах вычисления, которыми являются таблицы и формулы.
1 Чем усложняется расчет веса металла?
Кузнечное искусство давно отошло на второй план, и сегодня основным источником стальных, чугунных или медных изделий стала металлургия. Продукция проходит различные виды обработки, претерпевает изменения на всевозможных станках, однако следует разделять способы обработки. Прежде всего, это холодный и горячий прокат. Разница между ними огромна, поскольку воздействие на металл при высоких или низких температурных режимах дает определенные отличия в результатах. В частности, речь идет о геометрии проката.
Техпроцесс при обоих видах обработки один и тот же – заготовка размещается между двумя вращающимися в разных направлениях валами, которыми и прессуется до нужного состояния профиля. Ввиду того, что холодный прокат не связан с продолжительным нагревом металла до высоких температур, и обработка осуществляется в большей степени за счет механической нагрузки, а не пластичности материала, лист получается ровнее. Горячий прокат, наоборот, изготавливается при постоянной термообработке, обычно это твердые сплавы, имеющие незначительную пластичность.
Из-за непрерывного нагрева поверхность листов окисляется, рекристаллизация происходит неравномерно, поэтому разные участки горячекатаного изделия могут быть разной толщины.
Таким образом, становится очевидным, что точность расчетов второго типа металлопрофилей будет довольно относительной. Ведь погрешности в толщине вынуждают принять какую-то среднюю, приблизительную величину для этого значения. А безукоризненная геометрия листа, полученного при холодном прокате, позволит вычислить его вес с достаточной степенью точности. С другой стороны, масса горячекатаных изделий зачастую зависит от типа и калибра профиля, что позволяет не принимать во внимание небольшие отклонения при вычислениях. А значит, можно смело начинать вычисления или использовать готовый калькулятор расчета веса листа металла онлайн.
2 Как вычислить массу профиля прямоугольного сечения?
Наиболее распространенные типы профилей, с которыми приходится сталкиваться в быту – это, в первую очередь, металлические изделия круглого или прямоугольного сечения. К первым можно отнести прутки, арматуру, трубы, а второй тип – это полые профили с квадратным сечением, металлические балки, и даже обычный катаный лист входит в эту же категорию. Проще всего рассчитать изделия с прямоугольным профилем, поэтому начнем ознакомление с вычислением именно такого типа продуктов проката.
К первым можно отнести прутки, арматуру, трубы, а второй тип – это полые профили с квадратным сечением, металлические балки, и даже обычный катаный лист входит в эту же категорию. Проще всего рассчитать изделия с прямоугольным профилем, поэтому начнем ознакомление с вычислением именно такого типа продуктов проката.
Формула для определения массы любого металлического изделия, независимо от его сечения: m = pV, где p – плотность, а V – объем. Те, кто знаком с химией, знают: сколько существует химических элементов, столько же и соответствующих им плотностей. Следовательно, каждому металлу или сплаву соответствует определенная, характерная ему величина этого значения, которую можно узнать в ГОСТе. А вот объем надо высчитывать, причем исходя из формы профиля, для чего подключаются знания геометрии.
Сначала узнаем площадь сечения: для листа – перемножая толщину и ширину, для трубы квадратного сечения – складываем величины сторон и умножаем на толщину стенки. Затем умножаем результат на длину изделия. Таким образом, для листа у нас получается формула массы mЛ = ABLp, а вес квадратного профиля mКП = b2(A+B)Lp, где A и B – ширина сторон профиля, b – толщина стенки изделия, L – длина, а p – плотность металла.
Затем умножаем результат на длину изделия. Таким образом, для листа у нас получается формула массы mЛ = ABLp, а вес квадратного профиля mКП = b2(A+B)Lp, где A и B – ширина сторон профиля, b – толщина стенки изделия, L – длина, а p – плотность металла.
3 Определяем вес профиля круглого сечения
Очень часто для строительных работ приходится закупать пруток, арматуру и, конечно, трубы, без которых невозможно обеспечить снабжение дома холодной и горячей водой. Но предварительно нужно рассчитать массу металлического изделия, чтобы правильно организовать транспортировку.
Если вы приобретаете пруток или арматуру, все довольно просто, берем все ту же общую формулу для определения массы профиля m = pV, и все, что нам остается сделать – это найти объем.
Начинаем с вычисления площади сечения, которое, впрочем, отличается от расчетов для квадратного профиля. В данном случае формула будет выглядеть так: S = πD2/4. Результат умножаем на длину и получаем объем V = SL. В итоге m = (πD2/4)Lp. Так можно рассчитать любой вес стального круга: хоть проволоки, хоть арматуры. Массу последней можно узнать и из таблицы:
Диаметр арматуры | Вес 1 метра арматуры | Погонных метров в тонне |
d 6 | 0,222 | 4504,5 |
d 8 | 0,395 | 2531,65 |
d 10 | 0,617 | 1620,75 |
d 12 | 0,888 | 1126,13 |
d 14 | 1,21 | 826,45 |
d 16 | 1,58 | 632,91 |
d 18 | 2 | 500 |
d 20 | 2,47 | 404,86 |
d 22 | 2,98 | 335,57 |
d 25 | 3,85 | 259,74 |
d 28 | 4,83 | 207,04 |
d 32 | 6,31 | 158,48 |
d 36 | 7,99 | 125,16 |
d 40 | 9,87 | 101,32 |
d 45 | 12,48 | 80,13 |
d 50 | 15,41 | 64,89 |
d 55 | 18,65 | 53,62 |
d 60 | 22,19 | 45,07 |
d 70 | 30,21 | 33,1 |
d 80 | 39,46 | 25,34 |
Другое дело, если вам нужно рассчитать трубу круглого профиля. Здесь дело придется иметь уже с внутренним и внешним диаметром, а также с толщиной стенки. В основе всего будет лежать все та же формула массы, определяемой по произведению объема и плотности. Объем же, как вы помните, можно найти, перемножив площадь сечения и длину изделия.
Здесь дело придется иметь уже с внутренним и внешним диаметром, а также с толщиной стенки. В основе всего будет лежать все та же формула массы, определяемой по произведению объема и плотности. Объем же, как вы помните, можно найти, перемножив площадь сечения и длину изделия.
Второе значение определяется путем простейших измерений, а первое, то есть площадь сечения, находим по формуле S = π(D2 — d2)/4. Здесь D – внешний диаметр, а d – внутренний диаметр, которые мы определяем по формуле d = D — 2b, где b – толщина стенки профиля. В итоге формула массы трубы с круглым сечением будет выглядеть следующим образом: m = (π(D2 — (D — 2b)2)/4)Lp.
4 Как узнать массу шестигранного профиля?
Может случиться так, что вам придется столкнуться с профилем нестандартной формы сечения. К примеру, мы привыкли видеть на строительной площадке обычную круглую арматуру. Но иногда возникает необходимость в шестигранном прутке, который, надо отметить, используется крайне редко, ввиду специфической формы и, зачастую, как заготовка для производства различных изделий.
Но иногда возникает необходимость в шестигранном прутке, который, надо отметить, используется крайне редко, ввиду специфической формы и, зачастую, как заготовка для производства различных изделий.
В частности, многие могут помнить, как в школе на уроках труда из коротких срезов этого прутка изготавливались гайки. Проще всего найти массу такого профиля, зная его размер (номер), с помощью следующей таблицы:
размер | вес (кг) | размер | вес (кг) | размер | вес (кг) | размер | вес (кг) |
№10 | 0,68 | №20 | 2,72 | №32 | 6,96 | №48 | 15,66 |
№11 | 0,82 | №21 | 3 | №34 | 7,86 | №50 | 16,98 |
№12 | 0,98 | №22 | 3,29 | №36 | 8,81 | №52 | 18,4 |
№13 | 11,15 | №24 | 3,92 | №38 | 9,82 | №55 | 20,58 |
№14 | 1,33 | №25 | 4,25 | №40 | 10,86 | №57 | 22,35 |
№15 | 1,53 | №26 | 4,59 | №41 | 11,54 | №60 | 24,5 |
№16 | 1,74 | №27 | 4,96 | №42 | 11,99 | ||
№17 | 1,96 | №28 | 5,33 | №43 | 12,71 | ||
№18 | 2,2 | №29 | 5,27 | №46 | 14,53 | ||
№19 | 2,45 | №30 | 6,12 | №47 | 14,95 |
Размер или, иначе говоря, номер шестигранника определяется по диаметру окружности, вписанной в сечение профиля, имеющее форму шестиугольника, то есть это расстояние между его противоположными сторонами. Готовых данных может не оказаться под рукой, и на этот случай лучше всего знать формулу, с помощью которой можно достаточно легко рассчитать массу шестигранного прутка. Как всегда, за основу принимаем m = pV.
Готовых данных может не оказаться под рукой, и на этот случай лучше всего знать формулу, с помощью которой можно достаточно легко рассчитать массу шестигранного прутка. Как всегда, за основу принимаем m = pV.
Для получения объема нам нужно узнать площадь сечения, которое имеет форму шестиугольника. Именно здесь мы сталкиваемся с основной сложностью, поскольку нужно будет высчитывать корни. Формула имеет следующий вид S = (3√3 . A2)/2, где А – ширина грани. Остается результат умножить на длину, и мы получаем объем, произведение которого с плотностью металла и даст нам массу, что в итоге будет выглядеть как m = ((3√3 . A2)/2)Lp.
Подобрать и приобрести необходимый металлопрокат можно на metalloprokat.navigator-beton.ru
КАК РАССЧИТАТЬ ВЕС МЕТАЛЛА — ФОРМУЛЫ И РЕКОМЕНДАЦИИ | Втормет-Регионы
При отсутствии возможности для непосредственного взвешивания, массу металлолома можно установить и иными путями. Наиболее точный результат даст расчёт, но не следует пренебрегать и другими возможностями.
Наиболее точный результат даст расчёт, но не следует пренебрегать и другими возможностями.
Итак, чтобы не грузить читателей лишними формулами, которые все же будут, но ниже, обозначим сразу формулы для расчета самых популярных изделий из стального проката и трубы — трубопроката. Здесь вы не найдете онлайн-калькулятора для расчета веса, лишь формулы, запомнив, которые 1 раз Вам больше не придется пользоваться специальными калькуляторами. Например, при демонтаже металлоконструкций или дымовой трубы, не всегда есть есть под рукой компьютер, интернет или справочник, а конструкции сварены все из сортового проката вот здесь и выручат наши формулы!
Формула, чтобы рассчитать вес трубы
M=(D-s)*s*0,02466
, где
M — масса одного погонного метра трубы, кг;
D — наружный диаметр рассчитываемой трубы, мм;
s — толщина стенки трубы, мм;
0,02466 —коэффициент при плотности стали равной 7,850 г/см3.

Эта формула очень точна. Вы можете рассчитать вес трубы и сверить расчетную массу с теоретической в любом сортаменте и значение по формуле будет точнее! Также можно вычислить
Рассчитываем вес листа металла
M=S*7,85
, где
M — масса стального листа, кг;
S — площадь вычисляемого листа, в метрах квадратных;
7,85 — вес листа толщиной 1 мм и площадью 1 метр квадратный, в килограммах
Так можно рассчитать вес листа металла любого размера, у которого Вы можете вычислить площадь. Точность расчетов по такой формуле выше, чем теоретическая масса в справочниках, т.к. в сортаменте при расчете массы металла программа округляет значения. Ну а как узнать площадь листа (любой формы — квадрата, прямоугольника, параллелепипеда, трапеции, ромба и т.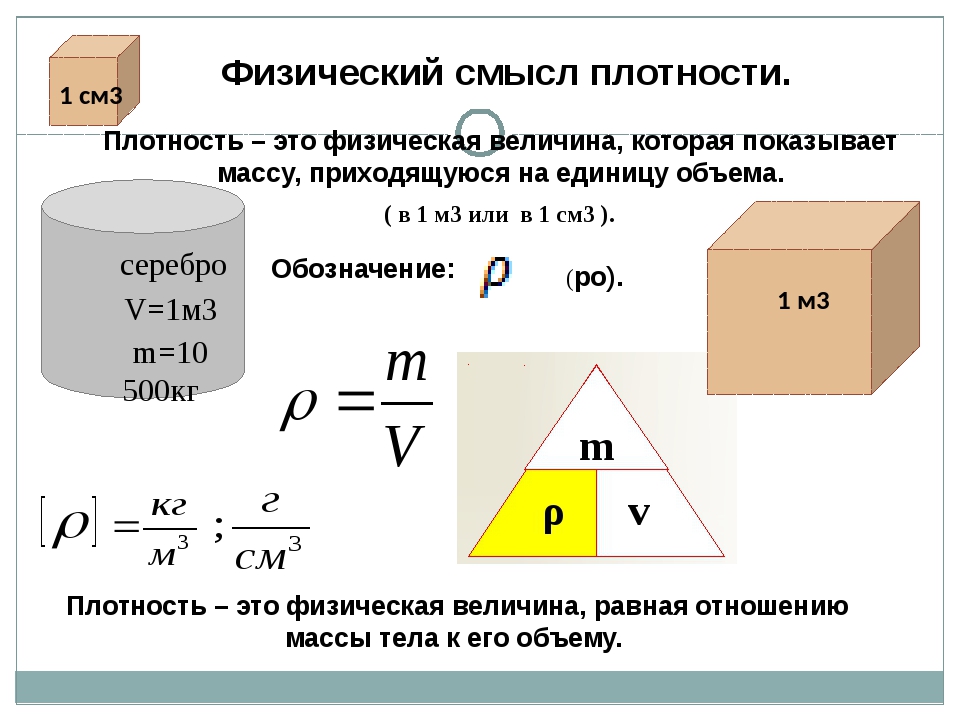 д. ) — должен знать каждый человек, окончивший среднюю школу.
д. ) — должен знать каждый человек, окончивший среднюю школу.
Как рассчитать вес арматуры и прутка
Для круга, прутка, гладкой арматуры формула для расчета массы будет такой:
M=(0,02466*D2)/4
, где
M — масса 1 погонного метра круга/арматуры/прутка, кг;
D — диаметр круга;
0,02466 —коэффициент при плотности стали равной 7,850 г/см3
Для расчета веса рифленой арматуры (А2, А3) можно и нужно использовать эту же формулу! Расхождений с теоретической массой не будет, не смотря на различные рисунки поперечных сечений.
Такую кучу металлолома, конечно, без взвешивания нереально посчитать по формулам
Общие подходы или немного скучной теории
Для определения веса любого предмета достаточно умножить его объём на удельный вес. Если с удельным весом всё более-менее понятно, то объём определить труднее (если не рассматривать такие простые формы как куб). Наиболее общим принципом расчёта объёма считается принцип Гюльдена, когда площадь поперечного сечения какого-либо предмета умножают на его высоту. С высотой металлоконструкции проблем также обычно не возникает, её легко (либо почти легко) замерить непосредственно, особенно, если сечение по высоте постоянно. Так можно поступить в отношении стальных труб любого сечения и профиля, двутавров, швеллеров, уголков и т.д. Метод определения массы металлических предметов сложных и непостоянных по высоте форм рассмотрим позднее.
Если с удельным весом всё более-менее понятно, то объём определить труднее (если не рассматривать такие простые формы как куб). Наиболее общим принципом расчёта объёма считается принцип Гюльдена, когда площадь поперечного сечения какого-либо предмета умножают на его высоту. С высотой металлоконструкции проблем также обычно не возникает, её легко (либо почти легко) замерить непосредственно, особенно, если сечение по высоте постоянно. Так можно поступить в отношении стальных труб любого сечения и профиля, двутавров, швеллеров, уголков и т.д. Метод определения массы металлических предметов сложных и непостоянных по высоте форм рассмотрим позднее.
Объём пирамиды
Пирамидальные окончания наверший стальных кованых заборов, дефлекторов и прочих частей металлоконструкций встречаются часто. Объём пирамиды легко рассчитать по формуле:
, где:
Поскольку в технике основаниями пирамиды могут служить квадрат, прямоугольник или треугольник, то проблема решается весьма просто.
Объём усечённой пирамиды
Форму усечённой пирамиды имеют ограждающие колпаки, защитные задвижки и дверцы. В таких ситуациях используется зависимость:
, где:
h – высота усечённой пирамиды;
F – площадь её большего основания;
f – площадь меньшего основания.
Если пирамидальная часть конструкции, сданной на металлолом, несколько деформирована, то недостающий объём добавляют или удаляют с каждой из сторон.
Объём клина и обелиска
Клин в технике часто является пятигранником, в основании которого лежит прямоугольник, а боковые грани являются равнобедренными треугольниками или трапециями. Формула для расчёта объёма клина имеет вид:
, где:
а – сторона основания подножия клина;
а1 – ширина верхушки клина;
b – толщина клина;
h — высота клина.

Обелиск — это шестигранник, основанием которого являются прямоугольники, которые расположены в параллельных плоскостях. Противоположные грани при этом симметрично наклонены к основанию обелиска. Объём данного геометрического тела:
, где:
а и b – размеры длины и ширины большего основания обелиска;
а а1 и b1 – меньшего основания обелиска;
h – высота обелиска.
Объём прутка и трубы
Для расчёта всех геометрических сечений, в основе которых лежит круг, не обойтись без параметра π – 3,14 (более высокая точность для металлолома и не требуется). Тогда для цилиндра имеем:
, где:
Для трубы (полого цилиндра) объём рассчитывается по формуле:
, где
r – внутренний радиус трубы.
Объём конуса и усечённого конуса
Геометрические формы конуса и усечённого конуса широко используются при конструировании деталей механизмов и машин. Объём конуса равен:
, где
Для вычисления объёма усечённого конуса используют более сложную зависимость:
, где
R – радиус меньшего основания конуса.
Объём сферических элементов металлоконструкций
Кроме собственно сферы, в практике приходится считать также объём шарового сегмента и сектора. Используются следующие зависимости:
Объёмы прокатных профилей
Чаще всего приходится определять вес тавров, двутавров, швеллеров, уголков. Для этого используются следующие зависимости:
Для тавра
,где b и b1 – соответственно ширина полки и стенки тавра; h и h2 – толщина основания и полки тавра; Н – высота таврового фрагмента лома;
Для двутавровой балки
,где Н – высота/длина двутаврового элемента; а – толщина стенки двутавра; с и с1 – толщина полки двутавра в основании и по торцу соответственно;
Для уголка
,где Н – длина уголка; l1 – толщина уголка; h2 и h3 соответственно – ширина каждой из полок.
Как установить массу конструкции особо сложной формы
Решение этой задачи возможно двумя способами. Согласно первому из них устанавливают значение так называемого коэффициента заполнения (способ применяется для габаритных узлов, разборка которых либо затруднительна, либо вовсе невозможна). Например, для ползунов кривошипных машин коэффициент заполнения принимают равным 0,3…0,35. Тогда считают массу узла G в предположении, что она сплошная, а затем умножают полученный результат на коэффициент заполнения.
Примерно такую же точность даёт эмпирическая формула Нистратова:
, где Р – номинальное усилие пресса в тоннах.
Оригинально можно установить массу небольших неразъёмных конструкций по объёму вытесненной ими воды. Для этого в тарированную ёмкость наливают до краёв воду. Устанавливают ёмкость в другую со значительно большим объёмом, а затем в первую ёмкость помещают данную конструкцию. Вытесненный ею объём воды взвешивают. Этот объём и будет равен объёму конструкции.
Вытесненный ею объём воды взвешивают. Этот объём и будет равен объёму конструкции.
Нейронные сети — математический аппарат
В наши дни возрастает необходимость в системах, которые способны не только выполнять однажды запрограммированную последовательность действий над заранее определенными данными, но и способны сами анализировать вновь поступающую информацию, находить в ней закономерности, производить прогнозирование и т.д. В этой области приложений самым лучшим образом зарекомендовали себя так называемые нейронные сети – самообучающиеся системы, имитирующие деятельность человеческого мозга. Рассмотрим подробнее структуру искусственных нейронных сетей (НС) и их применение в конкретных задачах.
Искусственный нейрон
Несмотря на большое разнообразие вариантов нейронных сетей, все они имеют общие черты. Так, все они, так же, как и мозг человека, состоят из большого числа связанных между собой однотипных элементов – нейронов, которые имитируют нейроны головного мозга. {-ax}}$, (3)
{-ax}}$, (3)
Основное достоинство этой функции в том, что она дифференцируема на всей оси абсцисс и имеет очень простую производную:
$f’\,(x) = \alpha f(x)\,\bigl(1\,-\,f\,(x)\bigr)$, (4)
При уменьшении параметра a сигмоид становится более пологим, вырождаясь в горизонтальную линию на уровне 0,5 при a=0. При увеличении a сигмоид все больше приближается к функции единичного скачка.
Нейронные сети обратного распространения
Нейронные сети обратного распространения – это мощнейший инструмент поиска закономерностей, прогнозирования, качественного анализа. Такое название – сети обратного распространения (back propagation) они получили из-за используемого алгоритма обучения, в котором ошибка распространяется от выходного слоя к входному, т. е. в направлении, противоположном направлению распространения сигнала при нормальном функционировании сети.
Нейронная сеть обратного распространения состоит из нескольких слоев нейронов, причем каждый нейрон слоя i связан с каждым нейроном слоя i+1, т. 2$, (5)
2$, (5)
где
yj – значение j-го выхода нейросети,
dj – целевое значение j-го выхода,
p – число нейронов в выходном слое.
Обучение нейросети производится методом градиентного спуска, т. е. на каждой итерации изменение веса производится по формуле:
$\Delta\,w_{ij} = -\,\eta\,\cdot\,\frac{\partial\,E}{\partial\,w_{ij}}$, (6)
где h – параметр, определяющий скорость обучения.
$\frac{\partial\,E}{\partial\,w_{ij}} = \frac{\partial\,E}{\partial\,y_i}\,\cdot\,\frac{dy_i}{dS_j}\,\cdot\,\frac{\partial\,S_j}{\partial\,w_{ij}}$, (7)
где
yj – значение выхода j-го нейрона,
Sj – взвешенная сумма входных сигналов, определяемая по формуле (1).
При этом множитель
$\frac{\partial\,S_j}{\partial\,w_{ij}} = x_i$, (8)
где
xi – значение i-го входа нейрона.
{(n)}\,(t\,-\,1)$ , (13.1)
Дополнительным преимуществом от введения момента является способность алгоритма преодолевать мелкие локальные минимумы.
Представление входных данных
Основное отличие НС в том, что в них все входные и выходные параметры представлены в виде чисел с плавающей точкой обычно в диапазоне [0..1]. В то же время данные предметной области часто имеют другое кодирование. Так, это могут быть числа в произвольном диапазоне, даты, символьные строки. Таким образом данные о проблеме могут быть как количественными, так и качественными. Рассмотрим сначала преобразование качественных данных в числовые, а затем рассмотрим способ преобразования входных данных в требуемый диапазон.
Качественные данные мы можем разделить на две группы: упорядоченные (ординальные) и неупорядоченные. Для рассмотрения способов кодирования этих данных мы рассмотрим задачу о прогнозировании успешности лечения какого-либо заболевания. Примером упорядоченных данных могут, например, являться данные, например, о дополнительных факторах риска при данном заболевании.
нет
ожирение
алкоголь
курение
гипертония
А также возможным примером может быть, например, возраст больного:
до 25 лет
25-39 лет
40-49 лет
50-59 лет
60 и старше
Опасность каждого фактора возрастает в таблицах при движении слева направо.
В первом случае мы видим, что у больного может быть несколько факторов риска одновременно. В таком случае нам необходимо использовать такое кодирование, при котором отсутствует ситуация, когда разным комбинациям факторов соответствует одно и то же значение. Наиболее распространен способ кодирования, когда каждому фактору ставится в соответствие разряд двоичного числа. 1 в этом разряде говорит о наличии фактора, а 0 о его отсутствии. Параметру нет можно поставить в соответствии число 0.
Таким образом для представления всех факторов достаточно 4-х разрядного двоичного числа. Таким образом число 10102 = 1010 означает наличие у больного гипертонии и употребления алкоголя, а числу 00002 соответствует отсутствие у больного факторов риска. Таким образом факторы риска будут представлены числами в диапазоне [0..15].
Во втором случае мы также можем кодировать все значения двоичными весами, но это будет нецелесообразно, т.к. набор возможных значений будет слишком неравномерным. В этом случае более правильным будет установка в соответствие каждому значению своего веса, отличающегося на 1 от веса соседнего значения. Так, число 3 будет соответствовать возрасту 50-59 лет. Таким образом возраст будет закодирован числами в диапазоне [0..4].
В принципе аналогично можно поступать и для неупорядоченных данных, поставив в соответствие каждому значению какое-либо число. Однако это вводит нежелательную упорядоченность, которая может исказить данные, и сильно затруднить процесс обучения.
В качестве одного из способов решения этой проблемы можно предложить поставить в соответствие каждому значению одного из входов НС. В этом случае при наличии этого значения соответствующий ему вход устанавливается в 1 или в 0 при противном случае. К сожалению, данный способ не является панацеей, ибо при большом количестве вариантов входного значения число входов НС разрастается до огромного количества. Это резко увеличит затраты времени на обучение. В качестве варианта обхода этой проблемы можно использовать несколько другое решение. В соответствие каждому значению входного параметра ставится бинарный вектор, каждый разряд которого соответствует отдельному входу НС.
Литература
- Dirk Emma Baestaens, Willem Max Van Den Bergh, Douglas Wood, «Neural Network Solution for Trading in Financial Markets», Pitman publishing
- R. M. Hristev, «Artifical Neural Networks»
- С. Короткий, «Нейронные сети: Алгоритм обратного распространения»
- С. Короткий, «Нейронные сети: Основные положения»
Формулы для вычисления массы тел различной формы
9.05.2013 // Владимир Трунов
Это странное название статьи объясняется только тем, что детали одной и той же формы могут быть как сплошными, так и полыми (т.е. следующая статья будет называться «Масса полой детали»).
Тут самое время вспомнить, что масса тела — это его объем , умноженный на плотность его материала (см. таблицы плотностей):
Объем сплошной детали — это… ее объем и больше ничего.Примечание. В приведенных ниже формулах все размеры измеряются в миллиметрах, а плотность — в граммах на кубический сантиметр.
Буквой обозначено отношение длины окружности к ее диаметру, составляющее примерно 3,14.Рассмотрим несколько простых форм (более сложные, как вы помните, можно составить путем сложения или вычитания простых).
1. Масса параллелепипеда (бруска)
Объем параллелепипеда: , где — длина, — ширина, — высота.
Тогда масса:2. Масса цилиндра
Объем цилиндра: , где — диаметр основания, — высота цилиндра.

Тогда масса:3. Масса шара
Объем шара: , где — диаметр шара.
Тогда масса:4. Масса сегмента шара
Объем сегмента шара: , где — диаметр основания сегмента, — высота сегмента.
Тогда масса:5. Масса конуса
Объем любого конуса: , где — площадь основания, — высота конуса.
Для круглого конуса: , где — диаметр основания, — высота конуса.
Масса круглого конуса:6. Масса усеченного конуса
Поскольку невозможно объять необъятное, рассмотрим только круглый усеченный конус. Его объем — это разность объемов двух вложенных конусов: с основаниями и : , где , . После никому не интересных алгебраических преобразований получаем:
, где — диаметр большего основания, — диаметр меньшего основания, — высота усеченного конуса.
Отсюда масса:7. Масса пирамиды
Объем любой пирамиды равен одной трети произведения площади ее основания на высоту (то же самое, что и для конусов (часто мы не замечаем, насколько мироздание к нам благосклонно)): , где — площадь основания, — высота пирамиды.

Для пирамиды с прямоугольным основанием: , где — ширина, — длина, — высота пирамиды.
Тогда масса пирамиды:8. Масса усеченной пирамиды
Рассмотрим усеченную пирамиду с прямоугольным основанием. Ее объем — это разность объемов двух подобных пирамид с основаниями и : , где , .
Исчеркав половину тетрадного листа, получаем: , где , — ширина и длина большего основания, , — ширина и длина меньшего основания, — высота пирамиды.
И, оставив в покое остальную половину листа, исходя из одних соображений симметрии, мы можем написать еще одну формулу, которая отличается от предыдущей только заменой W на L и наоборот. В чем разница между длиной и шириной? Только в том, что мы их так назвали. Назовем наоборот и получим: .
Тогда масса усеченной прямоугольной пирамиды:или
Для пирамиды с квадратным основанием (, ) формула выглядит проще:
Формула веса— что такое формула для определения веса? Примеры
Формула веса используется для определения точного веса тела в определенном поле силы тяжести.
Вес — это сила, испытываемая любой массой под действием силы тяжести. Ньютон — это единица измерения веса в системе СИ. W используется для обозначения веса. Вес может варьироваться в зависимости от силы тяжести, испытываемой телом.
Что такое формула веса?
Вес объекта складывается из его массы и ускорения свободного падения.Основные формулы для определения веса: W = мг (Ньютон)
где,
- W — вес объекта в Ньютонах
- м — масса объекта в кг
- g — ускорение свободного падения. На Земле значение g составляет 9,8 м / с 2 .
Давайте посмотрим на применение формулы для определения веса в следующем разделе.
Хотите найти сложные математические решения за секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов.Cuemath находит решения простым и легким способом.
Забронируйте бесплатную пробную версию Класс
Пример формулы веса
Пример 1: Масса корпуса 50 кг.
Рассчитайте вес по формуле веса. (Подсказка: используйте g = 9,8 м / с 2 .
Решение:
Чтобы найти вес тела.
Масса = 50 кг (дана)
Используя формулу, чтобы найти вес,
W =
мг W = 50 × 9.8
W = 490 НОтвет: Вес корпуса 490 Н
Пример 2: Если вес тела на Луне составляет 500 Н, найдите его массу. Значение g на Луне составляет 1,62 м / с 2 .
Решение:
Чтобы найти массу тела.
Масса тела на Луне = 500 Н (дано)
Используя формулу, чтобы найти вес,
W =
мг Масса тела =
Вт / г Масса тела = 500/1.62
Масса корпуса = 308,64 кгОтвет: Масса корпуса 308,64 кг
Пример 3: Масса тела 50 кг, масса 490 Н. С помощью формулы веса докажите, что g = 9,8 м / с 2 .
Решение:
Доказать, g = 9,8 м / с 2
Масса корпуса = 490 Н (заданная)
Масса = 50 кг (дана)
Используя формулу, чтобы найти вес,
W =
мг г = Вт / м
г = 490/50
г = 9.8
Следовательно, доказано g = 9,8 м / с 2
Часто задаваемые вопросы о весовой формуле
Что такое «m» в весовой формуле?
Общая формула для определения веса имеет вид W = мг (Н / кг). Здесь m представляет собой массу объекта.
Что такое «g» в формуле веса?
Общая формула для определения веса имеет вид W = мг (Н / кг). Здесь «g» обозначает ускорение свободного падения. На Земле значение g составляет 9,8 м / с 2 .Это также известно как гравитационная постоянная.
Как рассчитать массу по формуле веса?
Если дан вес объекта, то, составив общую формулу веса, мы можем вычислить массу. Его можно выразить как произведение массы и ускорения свободного падения.
W =
мг M = W × g
M = Wg (кг). Здесь g — гравитационная постоянная с фиксированным значением (9,8 м / с 2 )Какая формула для расчета веса?
Для расчета веса используется общая формула, указанная ниже:
Вт = мг.
Где W — вес объекта, m — масса объекта, а g — ускорение свободного падения. На Земле значение g составляет 9,8 м / с 2 .
Оценка веса товара — NIOS
Rural Technology
По соглашению мы часто используем единицы, отличные от единиц СИ. Часто вещи продаются с использованием другого измерения. Например, железо продается на килограмм веса. Это означает, что хотя мы измеряем размер для изготовления «стола» по длине, нам все же необходимо измерить его вес.Для оценки работы мы должны рассчитать вес используемого угла. Формула для расчета приведена ниже:
Вес материала = Плотность материала × объем работы. Объем задания = Площадь поперечного сечения объекта × длина объект Плотность железа 7,87 г / см3 или 7870 кг / м3.
Пример:
1) Рассчитайте вес 100 см стального стержня диаметром 4 см. в длину. Диаметр = 10 см Площадь = p / 4 × D2 Площадь = 3,14 / 4 × (4 × 4) = 12,56 см2 Объем = Площадь × Длина = 12.56 × 100 = 1256 см3 Вес = Плотность × Объем = 7,87 × 1256 = 9884,72 г = 9,88 кг 2) Рассчитайте вес уголка 25 × 25 × 3 мм длиной 3 метра.
Длина = 25 мм = 2,5 см, толщина = 3 мм = 0,3 см, длина = 3 м = 300 см.
Площадь поперечного сечения = (Площадь вертикального поперечного сечения) + Площадь горизонтального поперечного сечения
= (длина × ширина) + (длина × ширина) = (2,5 × 0,3) + (2,5 × 0,3) = 1,5 см2 Длина = 3 метра. = 300 см Объем = Площадь × Длина = 1,5 × 300 = 450 см3 Вес = Плотность × Объем = 7.87 × 450 = 3541,5 г = 3,54 кг
Что вы узнали
В этой главе мы узнали об измерениях, типах измерений, основных и производных единицах. У нас есть исследования количественного и качественного измерения. Мы также обсудили единицы СИ и Международные стандарты единиц. Мы также обсудили факторы, влияющие на выбор инструментов, наименьшее количество инструментов. В конце мы научились рассчитывать вес товара.
Терминальные вопросы
1) Запишите факторы, влияющие на выбор средств измерений.2) Оцените вес утюга следующего размера. L = 3 метра, ширина = 0,5 метра, толщина = 5 см Плотность железа 7,87 г / см3 или 7870 кг / м3.
Ответ на вопросы Intext
1,1 1) Получили хороший урожай. Качественный 2) Получили 5 центнеров риса. Количественный 3) В этом году достаточно дождя. Качественный 4) В этом году у нас дождь 500мм. Количественный 5) Эта конструкция требует много цемента. Качественный 6) Для этой конструкции необходимо 5 мешков цемента. Количественный 1.2 i) 0,5 м, 5500 м, 1,6 км, 1,02 м
ii) 1 кг 1.3 i) штангенциркуль, амперметр, термометр, весы ii) 0,01 см, 1 мм, 1 секунда
Предлагаемые мероприятия
1) Измерьте размеры своего дома. 2) Считайте и запишите различные параметры и единицы, написанные на бисквите или любом другом пакете.
Сельские технологии
Расчет теоретического веса
Расчет теоретического веса
- Пластина / Лист
- Пластина / листКруглая трубаКвадратная трубаПрямоугольная трубаПлоский стерженьШестигранный стерженьКруглый стерженьКруглый стерженьРавноугловой стерженьНеравноугольный стерженьФормула
- Плотность
- Нержавеющая сталь 304 (плотность 7.
93) Углеродистая сталь (Плотность 7,85) Алюминий (Плотность 2,7) Алюминий 1050, 1050A (Плотность 2,71) Алюминий 1060 (Плотность 2,71) Алюминий 1100 (Плотность 2,71) Алюминий 1145 (Плотность 2,7) Алюминий 1200 (Плотность 2,7) Алюминий 1235 (Плотность 2,71 ) Алюминий 2014 (плотность 2,8) Алюминий 2017 (плотность 2,79) Алюминий 2024 (плотность 2,78) Алюминий 3003 (плотность 2,73) Алюминий 3004 (плотность 2,72) Алюминий 3005 (плотность 2,73) Алюминий 3105 (плотность 2,72) Алюминий 5005 (плотность 2,7) Алюминий 5052 (плотность 2,68) Алюминий 5083 (плотность 2,66) Алюминий 5754 (плотность 2.67) Алюминий 6061 (плотность 2,7) Алюминий 6082 (плотность 2,7) Алюминий 7075 (плотность 2,81) Алюминий 8011 (плотность 2,71) Алюминий 8011A (плотность 2,71) Алюминий 8079 (плотность 2,72) Нержавеющая сталь 201 (плотность 7,93) Нержавеющая сталь 202 (плотность 7,93) Нержавеющая сталь 301 (плотность 7,93) Нержавеющая сталь 304L (плотность 7,93) Нержавеющая сталь 305 (плотность 7,93) Нержавеющая сталь 309S (плотность 7,98) Нержавеющая сталь 310S (плотность 7,98) Нержавеющая сталь 316 (плотность 7,98) Нержавеющая сталь 316L (плотность 7,98) ) Нержавеющая сталь 321 (плотность 7.
93) Нержавеющая сталь 347 (плотность 7,98) Нержавеющая сталь 405 (плотность 7,75) Нержавеющая сталь 409 (плотность 7,70) Нержавеющая сталь 410 (плотность 7,75) Нержавеющая сталь 420 (плотность 7,75) Нержавеющая сталь 430 (плотность 7,70) Нержавеющая сталь 434 (плотность 7,70) ) Алюминиевая шахматная пластина (плотность 2,9) г / см³
- Примечание: допуск по весу 0,2 ~ 0,7%
- Отправить [= (кг / шт) x общее количество шт x 0,001] = 0MT (метрические тонны)
Расчет молекулярной массы
- Отправить [= общий вес x 1000 / (кг / шт)] = 0PCS
— Центр Гельфанда
- Химическая формула воды — h3O, что означает, что эта молекула имеет 3 атома: 2 атома водорода (H) и 1 атом кислорода (O).Используя периодическую таблицу элементов, чтобы найти атомные веса, мы находим, что водород имеет атомный вес 1, а кислород — 16.
Чтобы вычислить молекулярный вес одной молекулы воды, мы складываем вклады от каждого атома; то есть 2 (1) + 1 (16) = 18 грамм / моль.
- Химическая формула мономера этилена — (Ch3-Ch3) -. Всего в нем 6 атомов: 2 атома углерода (C) и 4 атома водорода (H). Атомный вес углерода 12; а водород равен 1, поэтому один мер этилена имеет вес 2 (12) + 4 (1) = 28.Мы объединяем (реагируем) многие меры этилена вместе, образуя полиэтиленовую цепь. Одна тысяча мер, соединенных вместе, в сумме даст вес 28000 грамм / моль и будет иметь 6000 атомов.
моль — это стандартный химический метод определения количества присутствующего вещества. моль — это единица измерения количества вещества. Один моль «чего-то» содержит 6,022 x 1023 объекта. Например, в одном молях химического соединения 6.022 х 1023 молекул.
Рассчитаем молекулярную массу некоторых распространенных соединений. Используйте приведенную ниже таблицу, чтобы найти атомный вес каждого атома (элемента), или обратитесь к Периодической таблице элементов.
Подсказка : Подсчитайте количество атомов каждого элемента, а затем умножьте это число на атомный вес элемента.
Элемент Atomic
ВесH (водород) 1 C (углерод) 12 N (азот) 14 O (кислород) 16 Na (натрий) 23 Cl (хлор) 35
- Поваренная соль — NaCl
Ответ: 23 (1) +35 (1) = 58- Аммиак — Nh4
Ответ: 1 (3) +14 (1) = 3 + 14 = 17- Уксус (уксусная кислота) — Ch4COOH
Ответ: 1 (4) +12 (2) +16 (2) = 4 + 24 + 32 = 603.2: Формула и молекулярная масса
Цели обучения
- Для определения эмпирической формулы соединения по его массовому составу.
- Вывести молекулярную формулу соединения на основе его эмпирической формулы.
Когда новое химическое соединение, такое как потенциально новое лекарство, синтезируется в лаборатории или выделяется из природного источника, химики определяют его элементный состав, его эмпирическую формулу и структуру, чтобы понять его свойства.В этом разделе основное внимание уделяется тому, как определить эмпирическую формулу соединения, а затем использовать ее для определения молекулярной формулы, если молярная масса соединения известна.
Формула и молекулярная масса
Вес по формуле вещества — это сумма атомных весов каждого атома в его химической формуле . Например, вода (H 2 O) имеет вес по формуле:
\ [2 \ times (1.0079 \; а.е.м.) + 1 \ times (15.9994 \; amu) = 18.01528 \; amu \]
Если вещество существует в виде дискретных молекул (как с атомами, которые химически связаны между собой ), то химическая формула — это , молекулярная формула , а вес формулы — , — это , молекулярная масса — .
Например, углерод, водород и кислород могут химически связываться с образованием молекулы сахара , глюкозы с химической и молекулярной формулой C 6 H 12 O 6 . Формульный вес и молекулярный вес глюкозы составляют:
\ [6 \ раз (12 \; amu) + 12 \ times (1.00794 \; amu) + 6 \ times (15.9994 \; amu) = 180.0 \; amu \]
Ионные вещества не связаны химически и не существуют в виде дискретных молекул. Однако они действительно объединяются в дискретных соотношениях ионов.Таким образом, мы можем описать их формулы масс, но не их молекулярные массы . Например, столовая соль (\ (\ ce {NaCl} \)) имеет формульный вес:
.\ [23,0 \; amu + 35,5 \; amu = 58,5 \; amu \]
Процентный состав по формулам
В некоторых типах анализов важно знать массовый процент каждого типа элемента в соединении. Закон определенных пропорций гласит, что химическое соединение всегда содержит одинаковую пропорцию элементов по массе; то есть процентный состав — процентное содержание каждого элемента, присутствующего в чистом веществе — составляет , константа (хотя есть исключения из этого закона).
.Возьмем, например, метан (\ (CH_4 \)) с формулой и молекулярной массой:
\ [1 \ times (12.011 \; amu) + 4 \ times (1.008) = 16.043 \; amu \]
относительные (массовые) проценты углерода и водорода равны
\ [\% C = \ dfrac {1 \ times (12.011 \; amu)} {16.043 amu} = 0,749 = 74.9 \% \]
\ [\% H = \ dfrac {4 \ times (1.008 \; amu)} {16.043 \; amu} = 0,251 = 25,1 \% \]
Более сложным примером является сахароза (столовый сахар), которая содержит 42,11% углерода, 6,48% водорода и 51%.41% кислорода по массе. Это означает, что 100,00 г сахарозы всегда содержат 42,11 г углерода, 6,48 г водорода и 51,41 г кислорода. Сначала молекулярная формула сахарозы (C 12 H 22 O 11 ) используется для расчета массового процента составляющих элементов; затем массовый процент можно использовать для определения эмпирической формулы .
Согласно молекулярной формуле каждая молекула сахарозы содержит 12 атомов углерода, 22 атома водорода и 11 атомов кислорода.
Следовательно, моль молекул сахарозы содержит 12 моль атомов углерода, 22 моль атомов водорода и 11 моль атомов кислорода. Эта информация может использоваться для расчета массы каждого элемента в 1 моль сахарозы, что дает молярную массу сахарозы. Эти массы затем можно использовать для расчета процентного состава сахарозы. С точностью до трех десятичных знаков вычисления следующие:
\ [\ text {масса C / моль сахарозы} = 12 \, моль \, C \ times {12.011 \, г \, C \ over 1 \, mol \, C} = 144.132 \, g \, C \ label {3.1.1a} \]
\ [\ text {масса H / моль сахарозы} = 22 \, моль \, H \ times {1,008 \, г \, H \ over 1 \, mol \, H} = 22,176 \, г \, H \ label {3.1.1b} \]
\ [\ text {масса O / моль сахарозы} = 11 \, моль \, O \ times {15.999 \, g \, O \ over 1 \, mol \, O} = 175.989 \, g \, O \ label {3.1.1c} \]
Таким образом, 1 моль сахарозы имеет массу 342,297 г; Обратите внимание, что более половины массы (175,989 г) составляет кислород, а почти половина массы (144,132 г) — углерод.
Массовый процент каждого элемента в сахарозе — это масса элемента, присутствующего в 1 моль сахарозы, деленная на молярную массу сахарозы, умноженную на 100 для получения процента. Результат отображается с двумя десятичными знаками:
\ [\ text {мас.% C в сахарозе} = {\ text {масса C / моль сахарозы} \ over \ text {молярная масса сахарозы}} \ times 100 = {144,132 \, г \, C \ более 342,297 \, г / моль} \ раз 100 = 42,11 \% \]
\ [\ text {мас.% H в сахарозе} = {\ text {масса H / моль сахарозы} \ over \ text {молярная масса сахарозы}} \ times 100 = {22.176 \, г \, H \ более 342,297 \, г / моль} \ раз 100 = 6,48 \% \]
\ [\ text {мас.% O в сахарозе} = {\ text {масса O / моль сахарозы} \ over \ text {молярная масса сахарозы}} \ times 100 = {175.989 \, g \, O \ over 342.297 \, г / моль} \ раз 100 = 51,41 \% \]
Это можно проверить, убедившись, что сумма процентов всех элементов в составе составляет 100%:
\ [42,11 \% + 6,48 \% + 51,41 \% = 100,00 \% \]
Если сумма не 100%, в расчетах допущена ошибка.
Рисунок \ (\ PageIndex {1} \): процентный и абсолютный состав сахарозы(Однако округление до правильного числа десятичных знаков может привести к тому, что общая сумма будет немного отличаться от 100%.) Таким образом, 100,00 г сахарозы содержат 42,11 г углерода, 6,48 г водорода и 51,41 г кислорода; с точностью до двух знаков после запятой процентный состав сахарозы действительно составляет 42,11% углерода, 6,48% водорода и 51,41% кислорода.
Также можно рассчитать массовые проценты, используя атомные массы и молекулярные массы с атомными единицами массы.Поскольку ответ представляет собой соотношение, выраженное в процентах, единицы массы отменяют, являются ли они граммами (с использованием молярных масс) или атомными единицами массы (с использованием атомных и молекулярных масс).
Пример \ (\ PageIndex {1} \): NutraSweet
Аспартам — это искусственный подсластитель, продаваемый как NutraSweet and Equal. Его молекулярная формула \ (\ ce {C14h28N2O5} \).
Молекулярная структура аспартама. (CC BY-NC-SA 3.0; анонимно)
- Рассчитайте массовый процент каждого элемента в аспартаме.
- Рассчитайте массу углерода в пакете Equal 1,00 г, предполагая, что это чистый аспартам.
Дано : молекулярная формула и масса образца
Запрошено : массовый процент всех элементов и масса одного элемента в образце
Стратегия :
- Используйте атомные массы из периодической таблицы, чтобы вычислить молярную массу аспартама.
- Разделите массу каждого элемента на молярную массу аспартама; затем умножьте на 100, чтобы получить проценты.
- Чтобы найти массу элемента, содержащегося в заданной массе аспартама, умножьте массу аспартама на массовый процент этого элемента, выраженный в десятичной дроби.
Решение :
а.
A Мы вычисляем массу каждого элемента в 1 моль аспартама и молярную массу аспартама с точностью до трех знаков после запятой:
\ [14 \, C (14 \, моль \, C) (12.011 \, г / моль \, C) = 168.154 \, г \]
\ [18 \, H (18 \, моль \, H) (1.008 \, г / моль \, H) = 18,114 \, г \]
\ [2 \, N (2 \, моль \, N) (14.007 \, г / моль \, N) = 28.014 \, г \]
\ [+5 \, O (5 \, моль \, O) (15.999 \, г / моль \, O) = 79.995 \, г \]
\ [C_ {14} H_ {18} N_2O_5 \ text {молярная масса аспартама} = 294,277 \, г / моль \]
Таким образом, более половины массы 1 моля аспартама (294,277 г) составляет углерод (168,154 г).
B Чтобы вычислить массовый процент каждого элемента, мы разделим массу каждого элемента в соединении на молярную массу аспартама, а затем умножим на 100, чтобы получить проценты, которые здесь указаны с двумя десятичными знаками:
\ [масса \% \, C = {168.154 \, г \, С \ более 294,277 \, г \, аспартам} \ раз 100 = 57,14 \% С \]
\ [масса \% \, H = {18,114 \, г \, H \ более 294,277 \, г \, аспартам} \ раз 100 = 6,16 \% H \]
\ [масса \% \, N = {28,014 \, г \, N \ более 294,277 \, г \, аспартам} \ раз 100 = 9,52 \% \]
\ [масса \% \, O = {79,995 \, г \, O \ более 294,277 \, г \, аспартам} \ раз 100 = 27,18 \% \]
Для проверки мы можем сложить проценты:
\ [57,14 \% + 6,16 \% + 9.52 \% + 27,18 \% = 100,00 \% \]
Если вы получили итоговое значение, которое отличается от 100% более чем примерно на ± 1%, то в вычислении должна быть ошибка.
г. C Масса углерода в 1,00 г аспартама рассчитывается следующим образом:
\ [\ text {масса C} = 1,00 \, г \, аспартам \ times {57,14 \, г \, C \ более 100 \, г \, аспартам} = 0,571 \, г \, C \]
Упражнение \ (\ PageIndex {1} \): оксид алюминия
Рассчитайте массовый процент каждого элемента в оксиде алюминия (Al 2 O 3 ).Затем рассчитайте массу алюминия в 3,62 г образца чистого оксида алюминия.
- Ответ
52,93% алюминия; 47,08% кислорода; 1,92 г Al
Определение эмпирической формулы пенициллина
Так же, как эмпирическая формула вещества может использоваться для определения его процентного состава, процентный состав образца может использоваться для определения его эмпирической формулы, которая затем может использоваться для определения его молекулярной формулы.Такая процедура фактически использовалась для определения эмпирических и молекулярных формул первого открытого антибиотика: пенициллина.
Антибиотики — это химические соединения, которые избирательно убивают микроорганизмы, многие из которых вызывают заболевания. Хотя сегодня антибиотики часто воспринимаются как должное, пенициллин был открыт всего около 80 лет назад. Последующая разработка широкого спектра других антибиотиков для лечения многих распространенных заболеваний в значительной степени способствовала значительному увеличению продолжительности жизни за последние 50 лет.Открытие пенициллина — это исторический детектив, в котором ключевую роль сыграло использование массовых процентов для определения эмпирических формул.
В 1928 году Александр Флеминг, молодой микробиолог из Лондонского университета, работал с обычной бактерией, вызывающей фурункулы и другие инфекции, такие как заражение крови. Для лабораторных исследований бактерии обычно выращивают на поверхности геля, содержащего питательные вещества, в небольших плоских чашках для культивирования. Однажды Флеминг заметил, что одна из его культур была заражена голубовато-зеленой плесенью, похожей на плесень, обнаруженную на испорченном хлебе или фруктах.Такие несчастные случаи довольно часты, и большинство лабораторных работников просто выбросили бы культуры. Флеминг, однако, заметил, что бактерии растут на геле повсюду, кроме контаминационной плесени (часть (а) на рисунке \ (\ PageIndex {2} \)), и предположил, что плесень должна производить вещество, которое либо убили бактерии или предотвратили их рост. Чтобы проверить эту гипотезу, он вырастил плесень в жидкости, а затем отфильтровал жидкость и добавил ее к различным культурам бактерий.Жидкость убила не только бактерии, которые первоначально изучал Флеминг, но и множество других болезнетворных бактерий. Поскольку плесень была членом семейства Penicillium (названного по имени их карандашообразных ветвей под микроскопом) (часть (b) на рисунке \ (\ PageIndex {2} \)), Флеминг назвал активный ингредиент в бульоне пенициллином.
Рисунок \ (\ PageIndex {2} \): Penicillium. а) плесень Penicillium растет в культуральной посуде; на фото показано его влияние на рост бактерий. (b) На этой микрофотографии Penicillium видны его палочкообразные и карандашные ветви.Название происходит от латинского penicillus, что означает «кисть».Хотя Флемингу не удалось выделить пенициллин в чистом виде, медицинское значение его открытия стимулировало исследователей в других лабораториях. Наконец, в 1940 году два химика из Оксфордского университета, Говард Флори (1898–1968) и Эрнст Чейн (1906–1979), смогли выделить активный продукт, который они назвали пенициллин G. В течение трех лет пенициллин G получил широкое распространение. его использовали для лечения пневмонии, гангрены, гонореи и других заболеваний, а его использование значительно увеличило выживаемость раненых солдат во время Второй мировой войны.В результате своей работы Флеминг, Флори и Чейн разделили Нобелевскую премию по медицине в 1945 году.
Как только им удалось выделить чистый пенициллин G, Флори и Чейн подвергли это соединение процедуре, называемой анализом горения (описанной далее в этом разделе), чтобы определить, какие элементы присутствовали и в каких количествах. Результаты таких анализов обычно выражаются в массовых процентах. Они обнаружили, что типичный образец пенициллина G содержит 53,9% углерода, 4.8% водорода, 7,9% азота, 9,0% серы и 6,5% натрия по массе. Сумма этих чисел составляет всего 82,1%, а не 100,0%, что означает, что должен быть один или несколько дополнительных элементов. Разумным кандидатом является кислород, который является обычным компонентом соединений, содержащих углерод и водород; не думайте, что «недостающая» масса всегда связана с кислородом. Это может быть любой другой элемент. Однако по техническим причинам непосредственный анализ кислорода затруднен. Если предположить, что вся недостающая масса обусловлена кислородом, тогда пенициллин G содержит (100.0% — 82,1%) = 17,9% кислорода. Из этих массовых процентов можно определить эмпирическую формулу и, в конечном итоге, молекулярную формулу соединения.
Для определения эмпирической формулы из массовых процентов элементов в таком соединении, как пенициллин G, массовые проценты должны быть преобразованы в относительное количество атомов. Для удобства предположим, что образец соединения составляет 100,0 г, хотя размеры образцов, используемых для анализа, обычно намного меньше, обычно в миллиграммах.Это предположение упрощает арифметику, поскольку массовый процент углерода 53,9% соответствует 53,9 г углерода в 100,0 г образца пенициллина G; аналогично 4,8% водорода соответствует 4,8 г водорода в 100,0 г пенициллина G; и так далее для других элементов. Затем каждую массу делят на молярную массу элемента, чтобы определить, сколько молей каждого элемента присутствует в пробе 100,0 г:
\ [{масса \, (г) \ по молярной \, \, массе \, \, (г / моль)} = (г) \ влево ({моль \ по г} \ справа) = моль \ метка {3 .3.2a} \]
\ [53.9 \, g \, C \ left ({1 \, mol \, C \ over 12.011 \, g \, C} \ right) = 4.49 \, mol \, C \ label {3.3.2b} \ ]
\ [4.8 \, g \, H \ left ({1 \, mol \, H \ over 1.008 g \, H} \ right) = 4.8 \, mol \, H \ label {3.3.2c} \]
\ [7.9 \, g \, N \ left ({1 \, mol \, N \ over 14.007 \, g \, N} \ right) = 0.56 \, mol \, N \ label {3.3.2d} \ ]
\ [9 \, g \, S \ left ({1 \, mol \, S \ over 32.065 \, g \, S} \ right) = 0.28 \, mol \, S \ label {3.3.2e} \ ]
\ [6.5 \, g \, Na \ left ({1 \, mol \, Na \ over 22.990 \, g \, Na} \ right) = 0.28 \, mol \, Na \ label {3.3.2f} \]
Таким образом, 100,0 г пенициллина G содержит 4,49 моль углерода, 4,8 моль водорода, 0,56 моль азота, 0,28 моль серы, 0,28 моль натрия и 1,12 моль кислорода (при условии, что вся недостающая масса составляла кислород). Число значащих цифр в количестве молей элементов варьируется от двух до трех, потому что некоторые аналитические данные были представлены только двумя значащими цифрами.
Эти результаты дают отношения молей различных элементов в образце (4,49 моль углерода к 4,8 моль водорода и 0,56 моль азота и т. Д.), Но они не являются целочисленными отношениями, необходимыми для эмпирического расчета. формула — эмпирическая формула выражает относительное количество атомов в наименьших возможных целых числах. Чтобы получить целые числа, разделите количество молей всех элементов в образце на количество молей элемента, присутствующего в наименьшем относительном количестве, которым в данном примере является сера или натрий.Результатом будут индексы элементов в эмпирической формуле. С двумя значащими цифрами результаты таковы:
\ [C: {4.49 \ over 0.28} = 16 \, \, \, \, \, H: {4.8 \ over 0.28} = 17 \, \, \, \, \, N: {0.56 \ over 0.28 } = 2.0 \ label {3.3.3a} \]
\ [S: {0,28 \ более 0,28} = 1,0 \, \, \, \, \, Na: {0,28 \ более 0,28} = 1,0 \, \, \, \, \, O: {1,12 \ более 0,28 } = 4.0 \ label {3.3.3b} \]
Таким образом, эмпирическая формула пенициллина G имеет вид C 16 H 17 N 2 NaO 4 S.Другие эксперименты показали, что пенициллин G на самом деле является ионным соединением, которое содержит катионы Na + и анионы [C 16 H 17 N 2 O 4 S] — в соотношении 1: 1. Сложная структура пенициллина G (рисунок \ (\ PageIndex {3} \)) не была определена до 1948 года.
Рисунок \ (\ PageIndex {3} \): Структурная формула и шариковая модель аниона пенициллина G. В некоторых случаях один или несколько индексов в формуле, вычисляемой с помощью этой процедуры, могут не быть целыми числами.Означает ли это, что интересующее нас соединение содержит нецелое число атомов? Нет; Ошибки округления в расчетах, а также экспериментальные ошибки в данных могут привести к нецелым отношениям. Когда это происходит, необходимо принять решение при интерпретации результатов, как показано в примере 6. В частности, отношения 1,50, 1,33 или 1,25 предполагают, что вам следует умножить все индексы в формуле на 2, 3 или 4 соответственно. Только если отношение находится в пределах 5% от целого значения, следует рассмотреть возможность округления до ближайшего целого числа.
Пример \ (\ PageIndex {2} \): фосфат кальция в зубной пасте
Рассчитайте эмпирическую формулу ионного соединения фосфата кальция, основного компонента удобрений и полирующего агента в зубных пастах. Элементный анализ показывает, что он содержит 38,77% кальция, 19,97% фосфора и 41,27% кислорода.
Дано : процентное соотношение
Запрошено : эмпирическая формула
Стратегия :
- Возьмем образец весом 100 г и вычислим количество молей каждого элемента в этом образце.
- Получите относительное количество атомов каждого элемента в соединении, разделив количество молей каждого элемента в 100-граммовой пробе на количество молей элемента, присутствующего в наименьшем количестве.
- Если отношения не являются целыми числами, умножьте все нижние индексы на одно и то же число, чтобы получить целые значения.
- Поскольку это ионное соединение, определите анион и катион и запишите формулу так, чтобы заряды были сбалансированы.
Решение :
A В 100 г образца фосфата кальция содержится 38.77 г кальция, 19,97 г фосфора и 41,27 г кислорода. Разделив массу каждого элемента в образце 100 г на его молярную массу, можно получить количество молей каждого элемента в образце:
\ [\ text {моль Ca} = 38,77 \, г \, Ca \ times {1 \, моль \, Ca \ более 40,078 \, г \, Ca} = 0,9674 \, моль \, Ca \]
\ [\ text {моль P} = 19,97 \, г \, P \ times {1 \, моль \, P \ более 30,9738 \, г \, P} = 0,6447 \, моль \, Ca \]
\ [\ text {молей O} = 41,27 \, g \, O \ times {1 \, mol \, O \ более 15.9994 \, г \, О} = 2,5800 \, моль \, О \]
B Чтобы получить относительное количество атомов каждого элемента в соединении, разделите количество молей каждого элемента в 100-граммовой пробе на количество молей элемента в наименьшем количестве, в данном случае фосфора:
\ [P: {0,6447 \, моль \, P \ более 0,6447 \, моль \, P} = 1.000 \, \, \, \, Ca: {0,9674 \ более 0,6447} = 1,501 \, \, \, \ , O: {2,5800 \ более 0,6447} = 4,002 \]
C Мы могли бы записать эмпирическую формулу фосфата кальция как Ca 1.501 P 1.000 O 4.002 , но эмпирическая формула должна показывать отношения элементов в виде небольших целых чисел. Чтобы преобразовать результат в интегральную форму, умножьте все нижние индексы на 2, чтобы получить Ca 3,002 P 2,000 O 8,004 . Отклонение от интегральных атомных отношений невелико и может быть объяснено небольшими экспериментальными ошибками; следовательно, эмпирическая формула Ca 3 P 2 O 8 .
D Ион кальция (Ca 2 + ) является катионом, поэтому для поддержания электрической нейтральности фосфор и кислород должны образовывать многоатомный анион.Из главы 2 «Молекулы, ионы и химические формулы» мы знаем, что фосфор и кислород образуют фосфат-ион (PO 4 3-; см. Таблицу 2.4). Поскольку в эмпирической формуле присутствуют два атома фосфора, должны присутствовать два иона фосфата. Итак, запишем формулу фосфата кальция как Ca 3 (PO 4 ) 2 .
Упражнение \ (\ PageIndex {2} \): нитрат аммония
Вычислите эмпирическую формулу нитрата аммония, ионного соединения, содержащего 35.00% азота, 5,04% водорода и 59,96% кислорода по массе. Хотя нитрат аммония широко используется в качестве удобрения, он может быть взрывоопасным. Например, он был основным компонентом взрывчатки, использованной во время взрыва в Оклахома-Сити в 1995 году.
Федеральное здание Альфреда П. Мурра было разрушено в результате бомбардировки Оклахома-Сити с помощью химических взрывчатых веществ (быстрые химические реакции, в результате которых образуется огромное количество газов).
- Ответ
N 2 H 4 O 3 — это NH 4 + NO 3 — , записывается как NH 4 NO 3
От эмпирической формулы к молекулярной формуле
Эмпирическая формула дает только относительное число атомов в веществе в минимально возможном соотношении.Для ковалентного вещества химики обычно больше интересуются молекулярной формулой, которая дает фактическое количество атомов каждого типа, присутствующих в молекуле. Однако без дополнительной информации невозможно узнать, является ли формула пенициллина G, например, C 16 H 17 N 2 NaO 4 S или целым кратным, таким как C 32 H 34 N 4 Na 2 O 8 S 2 , C 48 H 51 N 6 Na 3 O 12 S 3 , или (C 16 H 17 N 2 NaO 4 S) n , где n — целое число.(Фактическая структура пенициллина G показана на рисунке \ (\ PageIndex {3} \)).
Рассмотрим глюкозу, сахар, который циркулирует в нашей крови, обеспечивая топливо для тела и мозга. Результаты анализа горения глюкозы показывают, что глюкоза содержит 39,68% углерода и 6,58% водорода. Поскольку горение происходит в присутствии кислорода, невозможно напрямую определить процентное содержание кислорода в соединении с помощью анализа горения; необходимы другие более сложные методы. Если предположить, что оставшийся процент приходится на кислород, тогда глюкоза будет содержать 53.79% кислорода. Таким образом, образец глюкозы весом 100,0 г будет содержать 39,68 г углерода, 6,58 г водорода и 53,79 г кислорода. Чтобы рассчитать количество молей каждого элемента в образце 100,0 г, разделите массу каждого элемента на его молярную массу:
\ [моль \, C = 39,68 \, g \, C \ times {1 \, mol \, C \ over 12.011 \, g \, C} = 3.304 \, mol \, C \ label {3.3.4a} \]
\ [моль \, H = 6.58 \, g \, H \ times {1 \, mol \, H \ over 1.0079 \, g \, H} = 6.53 \, mol \, H \ label {3.3.4b} \]
\ [молей \, O = 53,79 \, g \, O \ times {1 \, mol \, O \ over 15.9994 \, g \, O} = 3.362 \, mol \, O \ label {3.3.4c} \]
Еще раз, индексы элементов в эмпирической формуле находятся путем деления количества молей каждого элемента на количество молей элемента, присутствующего в наименьшем количестве:
\ [C: {3.304 \ over 3.304} = 1.000 \, \, \, \, H: {6.53 \ over 3.304} = 1.98 \, \, \, \, O: {3.362 \ over 3.304} = 1.018 \ ]
Отношение кислород: углерод равно 1.018, или приблизительно 1, а соотношение водород: углерод составляет приблизительно 2. Эмпирическая формула глюкозы, следовательно, CH 2 O, но какова ее молекулярная формула?
Многие известные соединения имеют эмпирическую формулу CH 2 O, включая формальдегид, который используется для сохранения биологических образцов и имеет свойства, которые сильно отличаются от сахара, циркулирующего в крови. На данный момент невозможно узнать, является ли глюкоза CH 2 O, C 2 H 4 O 2 или любой другой (CH 2 O) n .Однако экспериментально определенная молярная масса глюкозы (180 г / моль) может быть использована для решения этой дилеммы.
Сначала вычислите формульную массу, молярную массу формульной единицы, которая представляет собой сумму атомных масс элементов в эмпирической формуле, умноженную на их соответствующие индексы. Для глюкозы,
\ [\ text {формула массы} CH_2O = \ left [1 \, моль C \ left ({12.011 \, g \ over 1 \, mol \, C} \ right) \ right] + \ left [2 \ , mol \, H \ left ({1.0079 \, g \ over 1 \, mol \, H} \ right) \ right] + \ left [1 \, mol \, O \ left ({15.5994 \, mol \, O \ over 1 \, mol \, O} \ right) \ right] = 30,026 г \ label {3.3.5} \]
Это намного меньше наблюдаемой молярной массы 180 г / моль.
Во-вторых, определите количество формульных единиц на моль. Для глюкозы рассчитайте количество единиц (CH 2 O), то есть n в (CH 2 O) n , разделив молярную массу глюкозы на формульную массу CH 2 O :
\ [n = {180 \, г \ более 30,026 \, г / CH_2O} = 5,99 \ приблизительно 6 CH_2O \, \ text {формульные единицы} \ label {3.3.6} \]
Каждая глюкоза содержит шесть формульных единиц CH 2 O, что дает молекулярную формулу глюкозы (CH 2 O) 6 , которая чаще записывается как C 6 H 12 O 6 . Молекулярные структуры формальдегида и глюкозы, оба из которых имеют эмпирическую формулу CH 2 O, показаны на рисунке \ (\ PageIndex {4} \).
Рисунок \ (\ PageIndex {4} \): Структурные формулы и шаровые модели для (а) формальдегида и (б) глюкозыПример \ (\ PageIndex {3} \): Кофеин
Рассчитайте молекулярную формулу кофеина, соединения, содержащегося в кофе, чае и напитках колы, которое оказывает заметное стимулирующее действие на млекопитающих.Химический анализ кофеина показывает, что он содержит 49,18% углерода, 5,39% водорода, 28,65% азота и 16,68% кислорода по массе, а его экспериментально определенная молярная масса составляет 196 г / моль.
Дано : процентный состав и молярная масса
Запрошено : молекулярная формула
Стратегия :
- Допустим, 100 г кофеина. Из приведенных процентных соотношений используйте процедуру, приведенную в примере 6, для расчета эмпирической формулы кофеина.
- Рассчитайте массу по формуле, а затем разделите экспериментально определенную молярную массу на массу по формуле. Это дает количество присутствующих формульных единиц.
- Умножьте каждый индекс в эмпирической формуле на количество формульных единиц, чтобы получить молекулярную формулу.
Решение :
A Начнем с деления массы каждого элемента в 100,0 г кофеина (49,18 г углерода, 5,39 г водорода, 28,65 г азота, 16,68 г кислорода) на его молярную массу.Это дает количество молей каждого элемента в 100 г кофеина.
\ [моль \, C = 49,18 \, г \, C \ раз {1 \, моль \, C \ более 12,011 \, г \, C} = 4,095 \, моль \, C \]
\ [моль \, H = 5,39 \, г \, H \ раз {1 \, моль \, H \ более 1,0079 \, г \, H} = 5,35 \, моль \, H \]
\ [моль \, N = 28,65 \, г \, N \ раз {1 \, моль \, N \ более 14,0067 \, г \, N} = 2,045 \, моль \, N \]
\ [моль \, O = 16,68 \, г \, O \ раз {1 \, моль \, O \ более 15,9994 \, г \, O} = 1.043 \, моль \, О \]
Чтобы получить относительное количество атомов каждого присутствующего элемента, разделите количество молей каждого элемента на количество молей элемента, присутствующего в наименьшем количестве:
\ [O: {1.043 \ over 1.043} = 1.000 \, \, \, \, C: {4.095 \ over 1.043} = 3.926 \, \, \, \, H: {5.35 \ over 1.043} = 5.13 \ , \, \, \, N: {2.045 \ over 1.043} = 1.960 \]
Эти результаты достаточно типичны для реальных экспериментальных данных. Ни одно из атомных отношений не является точно целым, но все они находятся в пределах 5% от целых значений.Как и в примере 6, разумно предположить, что такие небольшие отклонения от целых значений вызваны небольшими экспериментальными ошибками, поэтому округлите их до ближайшего целого числа. Таким образом, эмпирическая формула кофеина: C 4 H 5 N 2 O.
B Молекулярная формула кофеина может быть C 4 H 5 N 2 O, но она также может быть любым целым кратным этому. Чтобы определить действительную молекулярную формулу, мы должны разделить экспериментально определенную молярную массу на формульную массу.Формула массы рассчитывается следующим образом:
\ [4C \, \, \, (4 \, атомы \, C) (12,011 \, г / атом \, C) = 48,044 \, г \]
\ [5H \, \, \, (5 \, атомы \, H) (1,0079 \, г / атом \, H) = 5,0395 \, г \]
\ [2N \, \, \, (2 \, атомы \, N) (14,0067 \, г / атом \, N) = 28,0134 \, г \]
\ [+ 1O \, \, \, (1 \, атом \, O) (15.9994 \, г / атом \, O) = 15.9994 \, г \]
\ [C_4H_5N_2O \, \, \, \, \ text {формула массы кофеина} = 97,096 \, г \]
Разделив измеренную молярную массу кофеина (196 г / моль) на расчетную массу по формуле, получим
\ [{196 г / моль \ более 97.096 г / C_4H_5N_2O} = 2,02 \ приблизительно 2 \, C_4H_5N_2O \, \ text {единицы эмпирической формулы} \]
C В кофеине две формулы C 4 H 5 N 2 O, поэтому молекулярная формула должна быть (C 4 H 5 N 2 O) 2 = C 8 H 10 N 4 O 2 . Состав кофеина следующий:
Упражнение \ (\ PageIndex {3} \): Хладон-114
Рассчитайте молекулярную формулу фреона-114, который имеет 13.85% углерода, 41,89% хлора и 44,06% фтора. Экспериментально измеренная молярная масса этого соединения составляет 171 г / моль. Как и фреон-11, фреон-114 является широко используемым хладагентом, который участвует в разрушении озонового слоя.
- Ответ
\ [C_2Cl_2F_4 \ nonumber \]
Сводка
Эмпирическая формула вещества может быть рассчитана на основе его процентного состава, а молекулярная формула может быть определена на основе эмпирической формулы и молярной массы соединения.Эмпирическая формула вещества может быть рассчитана на основе экспериментально определенного процентного состава, процентного содержания каждого элемента, присутствующего в чистом веществе по массе. Во многих случаях эти проценты можно определить анализом горения. Если молярная масса соединения известна, молекулярная формула может быть определена по эмпирической формуле.
Авторы и авторство
весовых формул |
Данные по давлению разрываДавление разрыва можно рассчитать по следующей формуле:
P = 2T x S, деленное на O.Д.P = Давление разрыва PSI | T = Толщина стенки трубы | O.D. = Внешний диаметр трубки
Информация о длине трубки
S = Предельная прочность материала (32 000 фунтов на квадратный дюйм для меди / 47 000 фунтов на квадратный дюйм для латуни)
Примечание: Рабочее давление на квадратный дюйм при 6-коэффициенте безопасности 6: 1 | Рабочий PSI @ 8-коэффициент запаса прочности 8: 1A. Фрезерные длины: Определенные одинаковые длины с установленными допусками с небольшими длинами, включенными в соответствии с установленным соглашением с заказчиком.
Вес на фут
B. Произвольная длина: Промежуточная длина без какой-либо указанной предпочтительной длины по согласованию с заказчиком.
C. Особые длины: Указанные одинаковые длины с учетом установленных допусков по длине (например: 12 футов — 0 дюймов, 9 футов — 7 дюймов или 0 — 4 1/2 дюйма от указанной длины). Если не указано иное, допуски соответствуют ASTM B251.Для определения веса (WT) на погонный фут бесшовной трубы, когда внешний диаметр (O.D.) дано:
Дополнительные формулы веса
A. Вычтите толщину стенки (T) из наружного диаметра, затем умножьте на толщину стенки. (O.D. — T) x T = Z
B. Используя полученное выше значение (Z), умножьте на 11,5736 для латуни или 12,1768 для меди .
Для латуни: Z x 11,5736 = Вес на погонный фут бесшовной медной трубы
Для меди: Z x 12,1768 = Вес на погонный фут бесшовной медной трубыD = Диаметр | Д.A. = Плотность сплава | I.D. = Внутренний диаметр | O.D. = Внешний диаметр
T = Толщина или толщина стенки | WT = вес | W = ширинаКРУГЛЫЙ СТЕРЖЕНЬ
Квадрат D x 9,42 x DA = Вес на погонный фут в фунтах.Квадратный стержень
Квадрат одной стороны x 12 x DA = вес на один линейный фут в фунтах.HEXAGON ROD
Квадратное расстояние между квартирами x 10.4 x DA = WT на линейный фут.ПРЯМОУГОЛЬНАЯ ШИНА
T x W x 12 x DA = WT на линейный фут в фунтах.КРУГЛАЯ ТРУБКА
37,7 x DA x T x OD — T = WT на линейный фут в фунтах.КВАДРАТНАЯ ТРУБКА
1,27 X WT круглой трубы с той же толщиной стенки и D, равным расстоянию между плоскостями квадратной трубы = WT на линейный фут.ЛИСТ
T x 144 x DA = WT на квадратный фут в фунтах.ПОЛОСЫ И РОЛИКИ
T x W x 12 x DA = вес на погонный фут в фунтах.КРУГОВ
Квадрат D x T x 0,785 x DA = WT окружности.КОЛЬЦА
НАД. + I.D. x O.D. — Я БЫ. х Т х 0,785 х Д.А. = Вес кольца в фунтах.Purina ONE SmartBlend Healthy Weight Formula Корм для взрослых премиум-класса
Характеристики
В нашем корме для собак здорового веса настоящая индейка является нашим первым ингредиентом. Почему? Потому что, хотя вы хотите, чтобы ваша собака сохраняла здоровый вес, она никогда не должна упускать из виду то, что ей не хватает.Конечно, в нашем рецепте меньше калорий, но он также со вкусом богат белком. Мы добавляем рис для получения энергии, а также полезные свойства сои для поддержания здорового веса. Именно выбор ингредиентов, которые работают вместе лучше, чем когда-либо сами по себе, вдохновил нас назвать этот сухой корм для собак SMARTBLEND.
Состав
Индейка (источник глюкозамина), рисовая мука, соевая мука, мука из кукурузной глютена, мука из куриных субпродуктов (источник глюкозамина), овсяная мука, цельнозерновая пшеница, мука из кукурузных зародышей, цельнозерновая кукуруза, мука из соевых зародышей, натуральный говяжий жир Содержит смесь токоферолов, глицерин, ароматизатор печени, карбонат кальция, соль, моно- и дикальцийфосфат, карамельный краситель, сушеную морковь, сушеный горох, хлорид калия, витамины [добавка витамина Е, ниацин (витамин B-3), добавка витамина А. , Пантотенат кальция (витамин B-5), мононитрат тиамина (витамин B-1), добавка витамина B-12, добавка рибофлавина (витамин B-2), гидрохлорид пиридоксина (витамин B-6), фолиевая кислота (витамин B-9). ), Комплекс бисульфита натрия менадиона (витамин К), добавка витамина D-3, биотин (витамин B-7)], минералы [сульфат цинка, сульфат железа, сульфат марганца, сульфат меди, йодат кальция, селенит натрия], хлорид холина, Моногидрохлорид L-лизина, сера.E-4175.Гарантированный анализ
Сырой протеин (мин.) … 27,0%
Сырой жир (мин.) … 8,0%
Сырой жир (макс.) … 12,0%
Сырая клетчатка (макс.) … 5,5%
Влажность (макс.) … 12,0%
Линолевая кислота (мин.) … 1,3%
Кальций (Ca) (мин.) … 0,9%
Фосфор (P) (мин) … 0,7%
Цинк (Zn) (мин.) … 150 мг / кг
Селен (Se) (мин.) … 0,35 мг / кг
Витамин А (мин.) … 13000 МЕ / кг
Витамин Е (мин.).. 250 МЕ / кг
Глюкозамин * (мин) … 350 частей на миллион
Омега-6 жирные кислоты * (мин.) … 1,5%.Инструкции по кормлению
ИНСТРУКЦИИ ПО КОРМЛЕНИЮ ИНСТРУКЦИИ ПО КОРМЛЕНИЮ ВЗРОСЛЫХ СОБАК Указанные рекомендуемые количества корма основаны на средних пищевых потребностях взрослой собаки, которая старше, менее активна или находится не в идеальном состоянии тела (с использованием стандартной мерной чашки 250 мл, которая содержит примерно 96 г Purina ONE. ). Такие факторы, как метаболизм собаки, размер породы, уровень активности, возраст, стерилизация или стерилизация собаки, будут влиять на количество Purina ONE, необходимое для достижения идеального состояния тела.Эксперты Purina в качестве отправной точки предоставили количество корма, указанное в столбце «Поддержание веса». Если вы обнаружите, что ваша собака имеет тенденцию набирать вес при кормлении этим количеством, вам может потребоваться уменьшить ее потребление калорий, скармливая количество, рекомендованное в альтернативной колонке. Продолжайте соответственно корректировать количество корма, чтобы помочь вашей собаке достичь идеальной формы тела и поддерживать ее. Регулярно следите за его весом, следя за тем, чтобы его ребра легко прощупывались, а талия была видна при взгляде сверху.Достижение и поддержание идеального состояния тела может повлиять на здоровье вашей собаки на всю жизнь. ЭТО НЕ ДЛЯ ВСЕХ СОБАК Формула для здорового веса Purina ONE SmartBlend разработана специально для взрослых собак. Если у вас есть щенок, беременная или кормящая собака, кормите Purina ONE Healthy Puppy Formula. МОЖНО ПОДАВАТЬ СУХОЕ ИЛИ УВЛАЖНЕННОЕ Purina ONE можно кормить сухим или смешанным с водой. Если смешать, мы предлагаем одну часть жидкости на четыре части Purina ONE. ПЕРЕКЛЮЧЕНИЕ НА PURINA ONE Несмотря на то, что вам будет интересно увидеть, как Purina ONE может изменить вашу собаку, подождите 7–10 дней, чтобы облегчить переход вашей собаки с текущего корма.Каждый день просто кормите немного меньше предыдущей пищи и немного больше Purina ONE, пока вы не будете кормить только Purina ONE. Этот постепенный переход поможет избежать диетических расстройств. ДОБАВКИ НЕ ТРЕБУЮТСЯ Purina ONE обеспечивает 100% полноценное и сбалансированное питание для взрослых собак. Нет необходимости добавлять витамины, минералы или другие добавки, если это специально не рекомендовано ветеринаром. Пресная вода, правильное питание и ветеринарный уход Не забывайте ежедневно давать собаке свежую воду в чистом контейнере.Правильная диета, физические упражнения и ветеринарный уход — лучшие способы сохранить здоровье вашей собаки. Если ваша собака не проходила обследование в прошлом году, запишитесь на прием сегодня.

 67 × 10-11 м3 кг-1 с-2
67 × 10-11 м3 кг-1 с-2

 {(n)}\,(t\,-\,1)$ , (13.1)
{(n)}\,(t\,-\,1)$ , (13.1)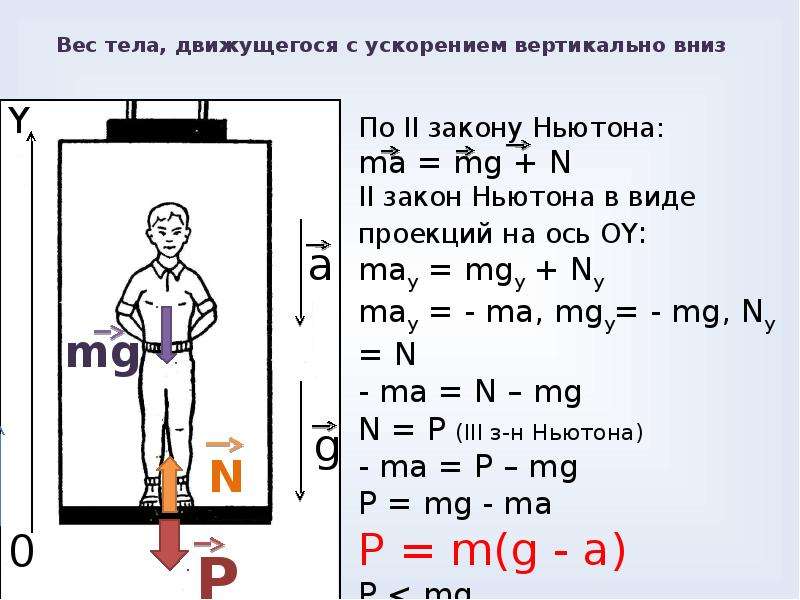
 Таким образом для представления всех факторов достаточно 4-х разрядного двоичного числа. Таким образом число 10102 = 1010 означает наличие у больного гипертонии и употребления алкоголя, а числу 00002 соответствует отсутствие у больного факторов риска. Таким образом факторы риска будут представлены числами в диапазоне [0..15].
Таким образом для представления всех факторов достаточно 4-х разрядного двоичного числа. Таким образом число 10102 = 1010 означает наличие у больного гипертонии и употребления алкоголя, а числу 00002 соответствует отсутствие у больного факторов риска. Таким образом факторы риска будут представлены числами в диапазоне [0..15]. В качестве одного из способов решения этой проблемы можно предложить поставить в соответствие каждому значению одного из входов НС. В этом случае при наличии этого значения соответствующий ему вход устанавливается в 1 или в 0 при противном случае. К сожалению, данный способ не является панацеей, ибо при большом количестве вариантов входного значения число входов НС разрастается до огромного количества. Это резко увеличит затраты времени на обучение. В качестве варианта обхода этой проблемы можно использовать несколько другое решение. В соответствие каждому значению входного параметра ставится бинарный вектор, каждый разряд которого соответствует отдельному входу НС.
В качестве одного из способов решения этой проблемы можно предложить поставить в соответствие каждому значению одного из входов НС. В этом случае при наличии этого значения соответствующий ему вход устанавливается в 1 или в 0 при противном случае. К сожалению, данный способ не является панацеей, ибо при большом количестве вариантов входного значения число входов НС разрастается до огромного количества. Это резко увеличит затраты времени на обучение. В качестве варианта обхода этой проблемы можно использовать несколько другое решение. В соответствие каждому значению входного параметра ставится бинарный вектор, каждый разряд которого соответствует отдельному входу НС. 05.2013 // Владимир Трунов
05.2013 // Владимир Трунов 

 Вес — это сила, испытываемая любой массой под действием силы тяжести. Ньютон — это единица измерения веса в системе СИ. W используется для обозначения веса. Вес может варьироваться в зависимости от силы тяжести, испытываемой телом.
Вес — это сила, испытываемая любой массой под действием силы тяжести. Ньютон — это единица измерения веса в системе СИ. W используется для обозначения веса. Вес может варьироваться в зависимости от силы тяжести, испытываемой телом. Рассчитайте вес по формуле веса. (Подсказка: используйте g = 9,8 м / с 2 .
Рассчитайте вес по формуле веса. (Подсказка: используйте g = 9,8 м / с 2 . 8
8 Где W — вес объекта, m — масса объекта, а g — ускорение свободного падения. На Земле значение g составляет 9,8 м / с 2 .
Где W — вес объекта, m — масса объекта, а g — ускорение свободного падения. На Земле значение g составляет 9,8 м / с 2 . Длина = 25 мм = 2,5 см, толщина = 3 мм = 0,3 см, длина = 3 м = 300 см.
Длина = 25 мм = 2,5 см, толщина = 3 мм = 0,3 см, длина = 3 м = 300 см.
 93) Углеродистая сталь (Плотность 7,85) Алюминий (Плотность 2,7) Алюминий 1050, 1050A (Плотность 2,71) Алюминий 1060 (Плотность 2,71) Алюминий 1100 (Плотность 2,71) Алюминий 1145 (Плотность 2,7) Алюминий 1200 (Плотность 2,7) Алюминий 1235 (Плотность 2,71 ) Алюминий 2014 (плотность 2,8) Алюминий 2017 (плотность 2,79) Алюминий 2024 (плотность 2,78) Алюминий 3003 (плотность 2,73) Алюминий 3004 (плотность 2,72) Алюминий 3005 (плотность 2,73) Алюминий 3105 (плотность 2,72) Алюминий 5005 (плотность 2,7) Алюминий 5052 (плотность 2,68) Алюминий 5083 (плотность 2,66) Алюминий 5754 (плотность 2.67) Алюминий 6061 (плотность 2,7) Алюминий 6082 (плотность 2,7) Алюминий 7075 (плотность 2,81) Алюминий 8011 (плотность 2,71) Алюминий 8011A (плотность 2,71) Алюминий 8079 (плотность 2,72) Нержавеющая сталь 201 (плотность 7,93) Нержавеющая сталь 202 (плотность 7,93) Нержавеющая сталь 301 (плотность 7,93) Нержавеющая сталь 304L (плотность 7,93) Нержавеющая сталь 305 (плотность 7,93) Нержавеющая сталь 309S (плотность 7,98) Нержавеющая сталь 310S (плотность 7,98) Нержавеющая сталь 316 (плотность 7,98) Нержавеющая сталь 316L (плотность 7,98) ) Нержавеющая сталь 321 (плотность 7.
93) Углеродистая сталь (Плотность 7,85) Алюминий (Плотность 2,7) Алюминий 1050, 1050A (Плотность 2,71) Алюминий 1060 (Плотность 2,71) Алюминий 1100 (Плотность 2,71) Алюминий 1145 (Плотность 2,7) Алюминий 1200 (Плотность 2,7) Алюминий 1235 (Плотность 2,71 ) Алюминий 2014 (плотность 2,8) Алюминий 2017 (плотность 2,79) Алюминий 2024 (плотность 2,78) Алюминий 3003 (плотность 2,73) Алюминий 3004 (плотность 2,72) Алюминий 3005 (плотность 2,73) Алюминий 3105 (плотность 2,72) Алюминий 5005 (плотность 2,7) Алюминий 5052 (плотность 2,68) Алюминий 5083 (плотность 2,66) Алюминий 5754 (плотность 2.67) Алюминий 6061 (плотность 2,7) Алюминий 6082 (плотность 2,7) Алюминий 7075 (плотность 2,81) Алюминий 8011 (плотность 2,71) Алюминий 8011A (плотность 2,71) Алюминий 8079 (плотность 2,72) Нержавеющая сталь 201 (плотность 7,93) Нержавеющая сталь 202 (плотность 7,93) Нержавеющая сталь 301 (плотность 7,93) Нержавеющая сталь 304L (плотность 7,93) Нержавеющая сталь 305 (плотность 7,93) Нержавеющая сталь 309S (плотность 7,98) Нержавеющая сталь 310S (плотность 7,98) Нержавеющая сталь 316 (плотность 7,98) Нержавеющая сталь 316L (плотность 7,98) ) Нержавеющая сталь 321 (плотность 7. 93) Нержавеющая сталь 347 (плотность 7,98) Нержавеющая сталь 405 (плотность 7,75) Нержавеющая сталь 409 (плотность 7,70) Нержавеющая сталь 410 (плотность 7,75) Нержавеющая сталь 420 (плотность 7,75) Нержавеющая сталь 430 (плотность 7,70) Нержавеющая сталь 434 (плотность 7,70) ) Алюминиевая шахматная пластина (плотность 2,9) г / см³
93) Нержавеющая сталь 347 (плотность 7,98) Нержавеющая сталь 405 (плотность 7,75) Нержавеющая сталь 409 (плотность 7,70) Нержавеющая сталь 410 (плотность 7,75) Нержавеющая сталь 420 (плотность 7,75) Нержавеющая сталь 430 (плотность 7,70) Нержавеющая сталь 434 (плотность 7,70) ) Алюминиевая шахматная пластина (плотность 2,9) г / см³ Чтобы вычислить молекулярный вес одной молекулы воды, мы складываем вклады от каждого атома; то есть 2 (1) + 1 (16) = 18 грамм / моль.
Чтобы вычислить молекулярный вес одной молекулы воды, мы складываем вклады от каждого атома; то есть 2 (1) + 1 (16) = 18 грамм / моль. Подсказка : Подсчитайте количество атомов каждого элемента, а затем умножьте это число на атомный вес элемента.
Подсказка : Подсчитайте количество атомов каждого элемента, а затем умножьте это число на атомный вес элемента.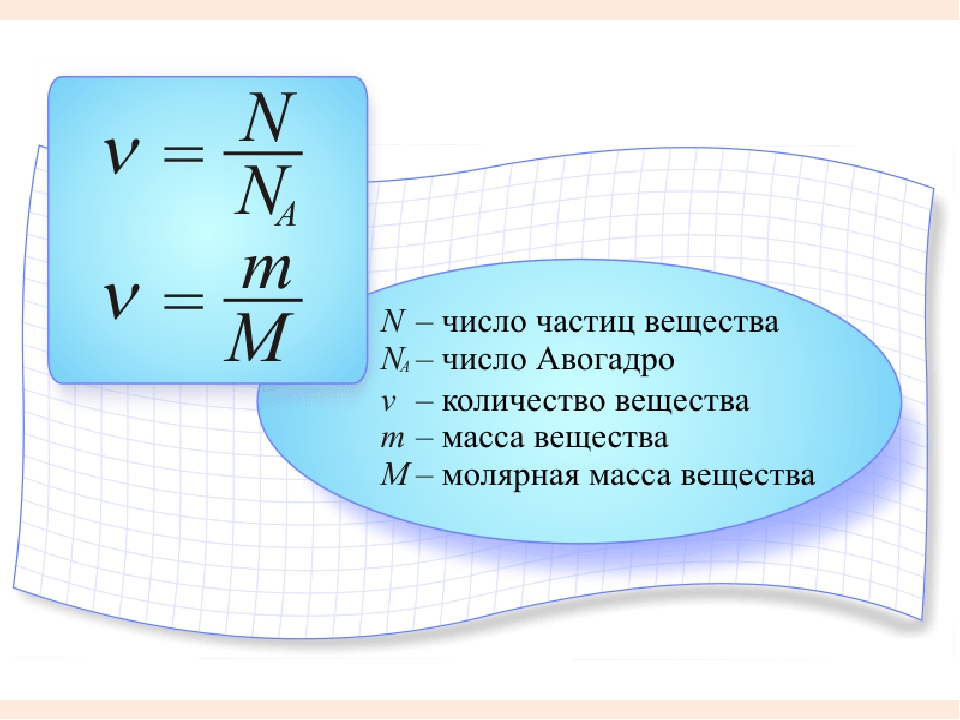
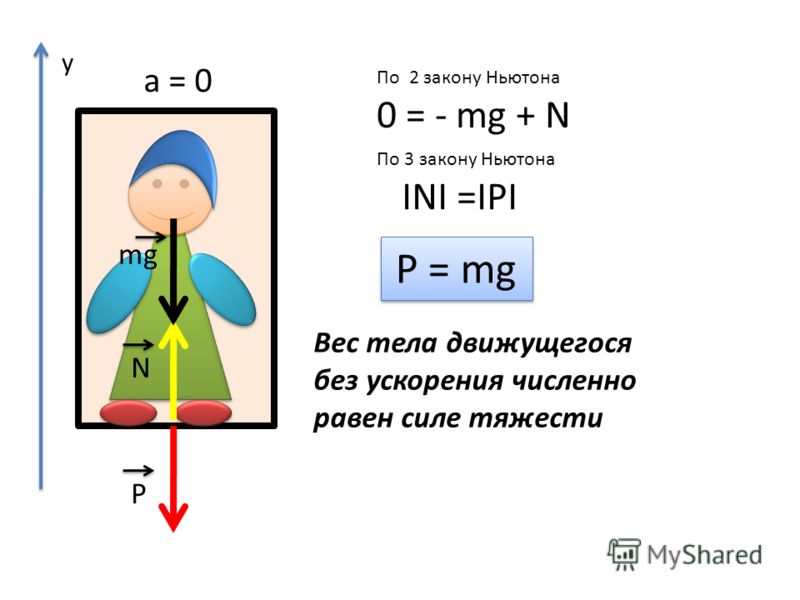 Например, углерод, водород и кислород могут химически связываться с образованием молекулы сахара , глюкозы с химической и молекулярной формулой C 6 H 12 O 6 . Формульный вес и молекулярный вес глюкозы составляют:
Например, углерод, водород и кислород могут химически связываться с образованием молекулы сахара , глюкозы с химической и молекулярной формулой C 6 H 12 O 6 . Формульный вес и молекулярный вес глюкозы составляют: Возьмем, например, метан (\ (CH_4 \)) с формулой и молекулярной массой:
Возьмем, например, метан (\ (CH_4 \)) с формулой и молекулярной массой: Следовательно, моль молекул сахарозы содержит 12 моль атомов углерода, 22 моль атомов водорода и 11 моль атомов кислорода. Эта информация может использоваться для расчета массы каждого элемента в 1 моль сахарозы, что дает молярную массу сахарозы. Эти массы затем можно использовать для расчета процентного состава сахарозы. С точностью до трех десятичных знаков вычисления следующие:
Следовательно, моль молекул сахарозы содержит 12 моль атомов углерода, 22 моль атомов водорода и 11 моль атомов кислорода. Эта информация может использоваться для расчета массы каждого элемента в 1 моль сахарозы, что дает молярную массу сахарозы. Эти массы затем можно использовать для расчета процентного состава сахарозы. С точностью до трех десятичных знаков вычисления следующие:
 (Однако округление до правильного числа десятичных знаков может привести к тому, что общая сумма будет немного отличаться от 100%.) Таким образом, 100,00 г сахарозы содержат 42,11 г углерода, 6,48 г водорода и 51,41 г кислорода; с точностью до двух знаков после запятой процентный состав сахарозы действительно составляет 42,11% углерода, 6,48% водорода и 51,41% кислорода.
(Однако округление до правильного числа десятичных знаков может привести к тому, что общая сумма будет немного отличаться от 100%.) Таким образом, 100,00 г сахарозы содержат 42,11 г углерода, 6,48 г водорода и 51,41 г кислорода; с точностью до двух знаков после запятой процентный состав сахарозы действительно составляет 42,11% углерода, 6,48% водорода и 51,41% кислорода.