Геометрические фигуры и их названия
Здесь вы с ребенком можете изучить геометрические фигуры и их названия с помощью веселых заданий в картинках. Но обучение будет проходить наиболее эффективно в том случае, если к распечатанному заданию вы добавите еще и различные образцы геометрических фигур. Для этой цели могут подойти такие предметы, как мячики, пирамидки, кубики, надутые воздушные шары (круглые и овальные), кружки для чая (стандартные, в форме цилиндра), апельсины, книги, клубки ниток, квадратные печенья и многое другое — все, что подскажет вам фантазия.
Все перечисленные предметы помогут ребенку понять, что значит объемная геометрическая фигура. Плоские фигуры можно подготовить, вырезав из бумаги нужные геометрические формы, предварительно раскрасив их в разные цвета.
Чем больше различных материалов вы подготовите для занятия, тем интереснее будет ребенку изучать новые для него понятия.
Также вам может понравиться наш онлайн тренажер по математике для 1 класса «Геометрические фигуры»:
Геометрические фигуры 1 класс — Онлайн-тренажер
Онлайн-тренажер по математике «Геометрические фигуры 1 класс» поможет первоклассникам потренироваться в умении различать основные геометрические фигуры: квадрат, круг, овал, прямоугольник и треугольник.
Геометрические фигуры и их названия — Проводим занятие с ребенком:
Чтобы легко и непринужденно ребенок смог запомнить геометрические фигуры и их названия, скачайте сначала картинку с заданием во вложениях внизу страницы, распечатайте на цветном принтере и положите на стол вместе с цветными карандашами. Также к этому времени у вас уже должны быть заготовлены различные предметы, которые мы перечисляли ранее.
- 1 этап. Сначала пусть ребенок выполнит задания на распечатанном листе — проговорит вслух названия фигур и раскрасит все картинки.
- 2 этап. Необходимо наглядно показать ребенку отличия объемных фигур от плоских. Для этого разложите все предметы-образцы (как объемные, так и вырезанные из бумаги) и отойдите с ребенком от стола на такое расстояние, с которого хорошо видны все объемные фигуры, но потерялись из виду все плоские образцы. Обратите внимание малыша на этот факт. Пусть он поэкспериментирует, подходя к столу то ближе, то дальше, рассказывая вам о своих наблюдениях.

- 3 этап. Дальше занятие нужно превратить в своеобразную игру. Попросите ребенка, чтобы он внимательно посмотрел вокруг себя и нашел предметы, которые имеют форму каких-либо геометрических фигур. Например, телевизор — прямоугольник, часы — круг и т.д. На каждой найденной фигуре — громко хлопайте в ладоши, чтобы добавить энтузиазма в игру.
- 4 этап. Проведите исследовательскую и наблюдательную работу с теми материалами-образцами, которые вы заготовили к занятию. Например, положите на стол книгу и плоский прямоугольник из бумаги. Предложите ребенку пощупать их, посмотреть на них с разных сторон и рассказать вам свои наблюдения. Таким же образом можно исследовать апельсин и бумажный круг, детскую пирамидку и бумажный треугольник, кубик и бумажный квадрат, воздушный шар овальной формы и овал, вырезанный из бумаги. Список предметов вы можете дополнить сами.
- 5 этап. Положите в непрозрачный пакет различные объемные образцы и попросите ребенка достать на ощупь квадратный предмет, затем круглый, затем прямоугольный и так далее.

- 6 этап. Разложите перед ребенком на столе несколько различных предметов из тех, которые участвуют в занятии. Затем пусть ребенок отвернется на несколько секунд, а вы спрячьте один из предметов. Повернувшись к столу ребенок должен назвать спрятанный предмет и его геометрическую форму.
Названия геометрических фигур — Карточки для распечатки
Изучая с малышом геометрические фигуры, вы можете использовать во время занятий карточки для распечатки от Лисёнка Бибуши. Скачайте вложения, распечатайте на цветном принтере бланк с карточками, вырежьте каждую карточку по контуру – и приступайте к обучению. Карточки можно заламинировать, либо наклеить на более плотную бумагу, чтобы сохранить внешний вид картинок, ведь использоваться они будут неоднократно.
Первые шесть карточек дадут вам возможность изучить с ребенком такие фигуры: овал, круг, квадрат, ромб, прямоугольник и треугольник, под каждой фигурой в карточках можно прочесть ее название.
После того, как ребенок запомнил название определенной фигуры, попросите его выполнить следующее: обвести по контуру все имеющиеся на карточке образцы изучаемой фигуры, а затем раскрасить их в цвет основной фигуры, расположенной в верхнем левом углу.
Скачать названия геометрических фигур — Карточки для распечатки — вы можете во вложениях внизу страницы
Карточки для распечатки с изображением плоских геометрических фигур
С помощью следующих шести карточек ребенок сможет познакомиться с такими геометрическими фигурами: параллелограмм, трапеция, пятиугольник, шестиугольник, звезда и сердце. Как и в предыдущем материале под каждой фигурой можно найти ее название.
Чтобы разнообразить занятия с малышом, совмещайте обучение с рисованием – такой метод не даст ребенку переутомиться, и малыш с удовольствием будет продолжать учебу. Следите за тем, чтобы обводя фигуры по черточкам, ребенок не спешил и выполнял задание аккуратно, ведь подобные упражнения не только развивают мелкую моторику, они могут повлиять в дальнейшем на почерк малыша.
Скачать карточки для распечатки с изображением плоских геометрических фигур вы можете во вложениях
Объемные геометрические фигуры и их названия — скачать карточки
В процессе, того, как вы будете изучать с ребенком объемные геометрические фигуры и их названия, используя новые шесть карточек от Бибуши с изображениями куба, цилиндра, конуса, пирамиды, шара и полусферы, приобретите изучаемые фигуры в магазине, либо воспользуйтесь предметами, находящимися в доме, имеющими подобную форму.
Покажите малышу на примерах, как в жизни выглядят объемные фигуры, ребенок должен потрогать и поиграть с ними. Прежде всего, это необходимо для того, чтобы задействовать наглядно – действенное мышление малыша, с помощью которого ребенку проще познавать окружающий мир.
Скачать — Объемные геометрические фигуры и их названия — вы можете во вложениях внизу страницы
Также вам будут полезны и другие материалы по изучению геометрических фигур:
Рисунки из геометрических фигур — Задания в картинках и раскраски
Веселые и красочные задания для детей «Рисунки из геометрических фигур» являются очень удобным обучающим материалом для детей дошкольного и младшего школьного возраста по изучению и запоминанию основных геометрических форм:
Геометрические фигуры — Раскраска для дошкольников
Задания ознакомят ребенка с основными фигурами геометрии — кругом, овалом, квадратом, прямоугольником и треугольником. Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска.
Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска.
Плоские геометрические фигуры — Обведи и дорисуй
Как правило, геометрию начинают изучать, рисуя плоские геометрические фигуры. Восприятие правильной геометрической формы невозможно без выведения ее своими руками на листе бумаги.
Найди формы геометрических фигур в картинках
Это занятие изрядно позабавит ваших юных математиков. Ведь теперь им придется находить знакомые формы геометрических фигур среди множества картинок.
Наложение фигур друг на друга — Задание для детей
Наложение фигур друг на друга — это занятие по геометрии для дошкольников и младших школьников. Смысл упражнения состоит в решении примеров на сложение. Только это необычные примеры. Вместо цифр здесь нужно складывать геометрические фигуры.
Свойства геометрических фигур для дошкольников
Это задание составлено в виде игры, в которой ребенку предстоит менять свойства геометрических фигур: форму, цвет или размер.
Счет геометрических фигур — Картинки с заданиями
Здесь вы можете скачать задания в картинках, в которых представлен счет геометрических фигур для занятий по математике.
Чертежи геометрических тел — Задание для детей
В этом задании ребенок познакомится с таким понятием, как чертежи геометрических тел. По сути, это занятие представляет собой мини-урок по начертательной геометрии
Геометрические фигуры из бумаги — Вырезаем и занимаемся
Здесь мы подготовили для вас объемные геометрические фигуры из бумаги, которые нужно вырезать и склеить. Куб, пирамиды, ромб, конус, цилиндр, шестигранник, распечатать их на картоне (или цветной бумаге, а затем наклеить на картон), а затем дать ребенку для запоминания.
Счет до 5 — Картинки с заданиями для малышей
Здесь мы выложили для вас счет до 5 — картинки с математическими заданиями для малышей, благодаря которым ваши дети потренируют не только свои навыки счета, но и умение читать, писать, различать геометрические фигуры, рисовать и раскрашивать.
И еще можете поиграть в математические игры онлайн от лисенка Бибуши:
Игра «Что лишнее? — Геометрические формы»
В этой развивающей онлайн игре ребенку предстоит определить, что является лишним среди 4 картинок. При этом необходимо руководствоваться признаками геометрических форм.
учим плоские и объемные геометрические фигуры
Масару Ибука в своей книге «После трёх уже поздно» утверждает, что в первые три года жизни у ребенка самый высокий потенциал к обучению и развитию, поэтому бездействие сродни преступлению.
Конечно, нам может казаться, что ребенок слишком мал. Да и чему он может научиться, если не умеет даже говорить? Но мозг ребёнка, как губка, впитывает всю окружающую его информацию. И от родителей зависит, что усвоит ребенок в этом возрасте.
Стоит ли начинать изучать геометрические фигуры в столь раннем возрасте? Безусловно. Ребенок живет в окружении геометрических форм. Знания, которые вы даёте, не должны быть оторваны от вашей повседневной жизни. Мама – проводник малыша в этом мире, и ей совершенно не обязательно иметь ученую степень, чтобы рассказать ребенку, как устроен мир.
Мама – проводник малыша в этом мире, и ей совершенно не обязательно иметь ученую степень, чтобы рассказать ребенку, как устроен мир.
Зачем ребенку учить геометрические фигуры?
Первые три года жизни ребенка – это период развития мозговых клеток, когда образуется прочная база для новых свершений. Уже в 3-4 месяца малыш способен различать формы. Это не означает, что пришла пора заучивать названия геометрических фигур, но мама при разговоре с крохой может стараться употреблять фразы: «А вот и наше любимое круглое блюдце», «Давай посмотрим, что в квадратной коробке» и подобные.
Знание геометрических фигур помогает:
- развивать пространственное мышление, ориентацию в пространстве;
- расширять кругозор;
- развивать способность сравнивать, анализировать, обобщать и выделять главное, классифицировать;
- пополнять словарный запас.
И, конечно же, полученные дошкольником знания послужат ему отличным подспорьем в изучении математики в школе.
Как учить геометрические фигуры с дошкольником?
- Обучение для дошкольников должно строиться в виде увлекательной игры.
- Не нужно ругать ребенка, если он не запомнил названия фигур с 1 раза, даже если с 31 – не стоит.
- Не забывайте органично вплетать геометрические познания в жизнь: «подай квадратную коробочку», «возьми яблоко с круглой тарелки».
- По дороге в сад ищите предметы прямоугольной или круглой формы, соревнуйтесь, кто больше найдет и назовет.
- В игровом арсенале у вас должны быть игрушки правильной геометрической формы — мячи, кубики, детали конструктора.
- Обычно малыши любят помогать маме на кухне. Приобретите круглые, квадратные, прямоугольные формочки и испеките съедобные геометрические фигуры.
- Важно при изучении фигур задействовать и тактильную память. Ребенку гораздо интереснее будет не только увидеть, но и пощупать, погладить, а может еще и лизнуть объект изучения.
- Нагружайте мозг ребёнка дозировано, постепенно дополняя информацией.
 Например, при изучении фигур повторяйте ещё и цвета: «Смотри, какой синий овал получился».
Например, при изучении фигур повторяйте ещё и цвета: «Смотри, какой синий овал получился».
Основные техники и методики запоминания фигур
Есть немало техник и методик, которые сделают запоминание фигур интересным для детей. Подбор методик будет зависеть от возраста и познаний ребёнка.
- До достижения 1,5 лет проговариваем вслух окружающие предметы, снабжая свой рассказ информацией о форме (давай возьмем круглое яблоко).
- В возрасте 1,5 — 2 лет пользуемся картинками, раскрашиваем фигуры, используем сортеры для изучения фигур. Начинаем с самого простого — круга. Остальные фигуры будем подключать только после того, как ребенок усвоил понятие «круг».
- С 2 лет до достижения школьного возраста можем применять все существующие методики, следуя от простого к сложному.
При изучении геометрических фигур, важно действовать поэтапно. Начать следует с легких фигур: круг, квадрат, треугольник, ромб, прямоугольник, овал. Знания этих фигур доступны для детей 2-3 лет.
Детки постарше, 4-5 лет, включают в свой лексикон и берут в оборот представления об трапеции, параллелограмме, пентагоне, гексагоне, октагоне, декагоне и других многоугольниках. Они уже умеют анализировать, поэтому с легкостью сравнивают и находят отличия между фигурами.
Старшие дошколята знакомятся с объемными фигурами: цилиндр, пирамида, куб, шар, конус, призма.
Разберем некоторые варианты техник по изучению геометрических фигур:
1. Сортер – ищем «домик» для каждой фигуры. Ребенок не только запомнит фигуры, но и будет развивать мелкую моторику вкупе с мышлением.
2. Лепка. Лепите вместе с малышом геометрические фигуры – лучшего занятия для развития мелкой моторики рук и усидчивости просто не придумаешь.
3. Объемные наклейки и магниты, изображающие геометрические фигуры, тоже могут помочь ребенку закрепить в памяти названия фигур.
4. Ищем половинки. Разрежьте геометрические фигуры на две части, смешайте и предложите малышу найти вторую половину.
Разрежьте геометрические фигуры на две части, смешайте и предложите малышу найти вторую половину.
5. Аппликации. Также из вырезанных фигур можно составлять геометрическую аппликацию. Например, домик (квадрат + треугольник), ёлочку, машинку.
6. Обводить пунктирные геометрические фигуры.
7. Раскрасить или заштриховать предложенные вами геометрические фигуры.
7. Дорисовать фигуру по образцу.
8. Рисовать фигуры при помощи трафаретов.
9. Послушать сказку, где главные герои — геометрические фигуры, а потом зарисовать услышанное.
10. Положить в непрозрачный мешок фигуры разной формы и предложить на ощупь угадать форму предмета.
11. Отличная игра для развития памяти и внимательности. Взрослый готовит вырезанные фигуры разных цветов и размеров и выкладывает перед малышом. Они обсуждают цвета, называют фигуры, а после взрослый прячет фигуру. Задача ребенка обнаружить и назвать, какой фигуры нет.
12. Выкладывание геометрических фигур при помощи счетных палочек или спичек. Когда ребенок овладеет этим навыком, можно перейти на более сложный уровень — решать задачки. Например, убери одну спичку так, чтобы получился треугольник.
13. Ассоциации. Предложите ребенку назвать предметы, на которые похож круг или прямоугольник.
14. Шнуровки и различные рамки-вкладыши, например, квадраты Никитина, где нужно из нескольких предметов воссоздать квадрат, либо доски Сегена, где необходимо вставить недостающую деталь.
15. Подвижные игры. Например, на асфальте рисуются овал, треугольник, квадрат, прямоугольник. По команде взрослого ребенок должен найти названную фигуру и встать в неё.
16. Видеоматериалы. Существует большое количество мультфильмов и обучающих материалов про геометрические фигуры. Посмотрите видео с малышом и обязательно обсудите увиденное.
17. Найдите в интернете и распечатайте картины, которые художники рисуют геометрическими формами, и предложите ребенку посчитать, сколько здесь кругов, прямоугольников и т. д.
д.
Учим объемные геометрические фигуры
Объемные фигуры можно изучать по аналогии с окружающим предметами (например, мяч = шар). И, конечно же, задействовать изучение предмета через игры:
- Найти объемную фигуру по плоскому образцу — отличное упражнение на развитие пространственного мышления.
- «Сыщик». Детям раздают «ориентировку» – плоский рисунок искомой фигуры со всех сторон. Детям необходимо сопоставить картинки и найти нужную фигуру.
- Создать трехмерную модель самому. Взрослый может распечатать трафареты с интернета. Ребенку остается согнуть по линиям и склеить, чтобы получилась фигура.
- Макеты, оригами – можно попробовать с вместе с ребенком создать свою объемную игрушку из бумаги.
- Конструктор. Постройте при помощи деталей башню или замок для принцессы. Эта игра будет способствовать развитию мелкой моторики, воображению, пониманию свойств объемных фигур.
Изучение геометрических фигур не должно становиться пыткой для ребенка и взрослого. Выбирайте ту методику, которая подходит именно вам. Проявите терпение и изобретательность, и тогда результат не заставит себя долго ждать. Главное, не забывайте поощрять ребенка за его новые открытия и время от времени повторять полученные знания.
Выбирайте ту методику, которая подходит именно вам. Проявите терпение и изобретательность, и тогда результат не заставит себя долго ждать. Главное, не забывайте поощрять ребенка за его новые открытия и время от времени повторять полученные знания.
Математика и логика для детей 7-13 лет
Развиваем логическое мышление через решение сюжетных математических задач в интерактивном игровом формате
узнать подробнеечто носить и как одеваться? Фото примеры 2021
Фигура дается при рождении, а уж потом женщины ее любят, совершенствуют или загоняют в тесные рамки, где неуютно, плохо и абсолютно не радостно. В результате собственное тело перестает нравиться и вызывает массу нареканий. Тип фигуры прямоугольник не отличается женственными изгибами и аппетитными формами, но именно такая внешность считается модельной. Если лишние килограммы или неуверенность мешают это заметить, будем ситуацию исправлять. Только не насилием над природой, а с помощью одежды. Правильно подобранный гардероб научит, как “сделать талию” там где нужно.
Только не насилием над природой, а с помощью одежды. Правильно подобранный гардероб научит, как “сделать талию” там где нужно.
В этой статье:
Фигура прямоугольник: характерные черты и подтипы
Иногда бывает затруднительно определить свой тип фигуры, так как в чистом виде они встречаются редко. Поможет сантиметровая лента или фото со спины в облегающей одежде. Итак, осмотр внешности показал:
- плечи и бедра равные по ширине;
- весьма призрачный намек на талию;
- плоские ягодицы;
- руки скорее тонкие, чем полные;
- стройные ноги, без признаков знаменитых «ушей» и прочих неприятностей.
Примите как должное, у вас прямоугольная фигура. К этому типу относятся и те, у кого талия имеется, но разница с бедрами составляет менее 20-22 сантиметров. Фигура делится на два подтипа – стройная колонна и истинный прямоугольник. Рассмотрим их особенности.
Стройная колонна:
- высокий рост;
- астеническое телосложение;
- угловатые плечи;
- маленькая грудь;
- тонкие руки.

Такие девушки практически не полнеют. Даже с течением возраста их силуэт напоминает мальчишеский.
Истинный прямоугольник:
- средний или небольшой рост;
- крупная грудь;
- слегка выступающий живот;
- при наборе веса увеличивается торс, низ остается относительно стройным;
- фигура в целом несколько мужеподобна.
Рост необязательный показатель. Он может варьировать в той и другой группе весьма значительно. А вот ноги обычно стройные и длинные.
Что скрыть, что продемонстрировать?
Ноги не единственное достоинство прямоугольника. У худой девушки, как правило, изящная форма плеч и ключиц, плоский живот, нет склонности к образованию целлюлита. Не грозит апельсиновая корка и в том случае, если дама достаточно полная. Излишняя массивность компенсируется спортивной статью, красивой грудью, правильными пропорциями.
Как ни крути, внешность довольно выигрышная, и есть что показать миру. А главное – женщины с типом фигуры прямоугольник могут особо не ограничивать себя в выборе фасонов.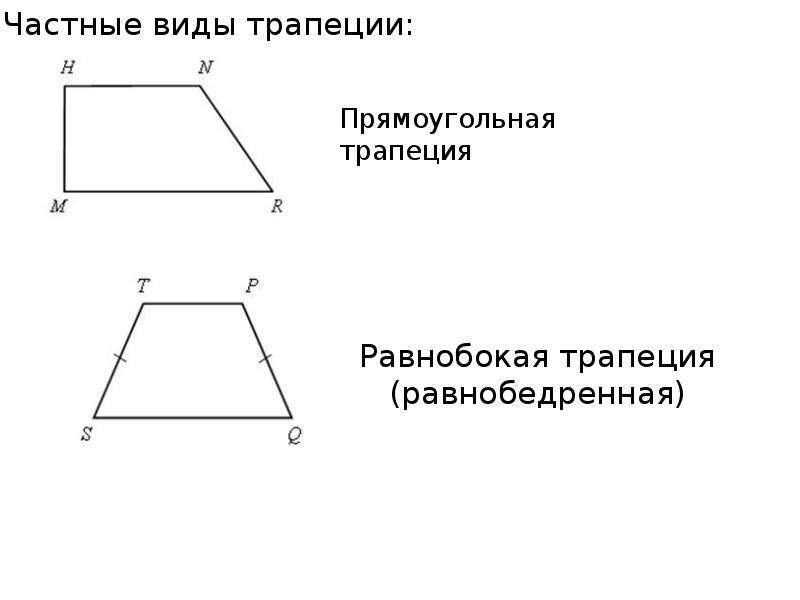 Им действительно идет практически все. Рельефным дамам (например, грушам) гораздо труднее выбрать одежду по фигуре. Здесь же всего одна проблема – отсутствие выраженной талии. Ее и будем решать.
Им действительно идет практически все. Рельефным дамам (например, грушам) гораздо труднее выбрать одежду по фигуре. Здесь же всего одна проблема – отсутствие выраженной талии. Ее и будем решать.
Как одеваться с худощавой и полной фигурой прямоугольник
Запаситесь терпением, вниманием и приступайте к изучению ответов на животрепещущий вопрос, как сделать талию с помощью различных предметов гардероба. Рекомендации в одежде для худых и полных прямоугольников будут отличаться лишь в одном аспекте. В остальном задается общее направление.
Девушки с типом внешности стройная колонна вполне могут носить одежду с акцентом на талии – юбки на широком поясе, мягкие кожаные ремни, а также стиль oversize. Но даже при незначительном лишнем весе от этих деталей лучше отказаться или использовать с осторожностью. Итак, начинаем создавать образы для фигуры прямоугольник.
Платье
Великая Коко Шанель, экстравагантная Жаклин Кеннеди, элегантная принцесса Диана тоже были прямоугольниками. Но они умели одеваться со вкусом и, конечно, выбирать фасоны платьев. Учитесь у них: пусть платье будет коротким, длинным, чуть ниже или выше колена.
Но они умели одеваться со вкусом и, конечно, выбирать фасоны платьев. Учитесь у них: пусть платье будет коротким, длинным, чуть ниже или выше колена.
Для повседневной носки подойдут:
- рубашечный и халатный крой;
- ретро из 20-х и 50-х годов;
- платье-футляр с баской;
- трапеция и А-силуэт;
- двухцветные с контрастными боковыми вставками;
- маленькие черные платья.
Для торжественных выходов выбирайте оригинальные и романтические фасоны. Вечерние платья в стиле ампир и асимметричные с одним плечом привлекут внимание к верхней части тела. Стройные ноги позволяют носить мини и эффектные высокие разрезы на моделях в пол. Идеальным дополнением будет принт или драпировка, сходящиеся к талии в форме Х.
Топы, туники, кардиганы
Для типа фигуры прямоугольник губительны топы на узких бретелях, укороченные, обтягивающие. Осторожно со сборками ампир. Неправильно подобранная длина – и вы ложно беременная. А вот крой в стиле блузона подойдет и для топов, и для трикотажных кофточек. Блузки лучше носить удлиненные, навыпуск, для смелых с оригинальным дополнением – корсетом сверху.
Осторожно со сборками ампир. Неправильно подобранная длина – и вы ложно беременная. А вот крой в стиле блузона подойдет и для топов, и для трикотажных кофточек. Блузки лучше носить удлиненные, навыпуск, для смелых с оригинальным дополнением – корсетом сверху.
Облегающие водолазки – только под жакет. Зато свободные демократичные туники – на все случаи жизни. Свитера оверсайз для стройных, остальным – чуть свободные укороченные модели. Интересно смотрятся теплые кофты на двусторонней молнии. Оставьте около 10 см не застегнутыми сверху и снизу, и вот уже Н-силуэт поменялся на гармоничный тип Х.
Подходят запахи, рюши, воланы в форме V и такие же вырезы. Горловина может быть овальной, лодочкой, полностью открывающей плечи, но не округлой под шею. Хорошим выбором станут полуприталенные жакеты, пиджаки, на одной пуговице. Прямоугольникам не страшна опасная для многих длина до самой широкой части бедер. Она не утяжеляет силуэт, а делает мягким.
Брюки, джинсы, шорты
Мешковатые штаны абсолютно не добавят женственных изгибов и объема. Аккуратные ягодицы лучше подчеркнуть облегающими моделями, классическими со складками, галифе, зрительно увеличить карманами, вышивками. Правило мешковатости не работает в отношении джинсов-бойфрендов. Бесшабашная модель и фигура прямоугольник просто созданы друг для друга.
Аккуратные ягодицы лучше подчеркнуть облегающими моделями, классическими со складками, галифе, зрительно увеличить карманами, вышивками. Правило мешковатости не работает в отношении джинсов-бойфрендов. Бесшабашная модель и фигура прямоугольник просто созданы друг для друга.
Джинсы подходят любые – скинни, классические, расклешенные. Это же относится к брюкам и к шортам. Самая разная длина, ширина, фактура, кроме тонких тканей, на этом типе фигуры сидят безупречно. Насторожить должна только посадка. Классическая и слишком низкая не годятся. Обе демонстрируют отсутствие бедер. Лучше выбрать умеренно низкую или завышенную.
Юбки
Идеальны силуэты трапеция, солнце-клеш, тюльпан – то, что делает форму бедер округлой. Не подойдут юбки с пышной сборкой от талии, а вот с небольшими защипами будет в самый раз. Молодым девушкам вполне уместно носить беззаботное мини, взрослым дамам лучше остановиться на элегантной длине в районе колена.
Стройные прямоугольники могут выбирать модели с широким поясом. Полным лучше предпочесть заниженную посадку или юбку на кокетке. Но все индивидуально, не забывайте о собственном комфорте. Хорошо сядет на узкие бедра юбка-карандаш. Пусть она будет на завышенной талии или без пояса.
Полным лучше предпочесть заниженную посадку или юбку на кокетке. Но все индивидуально, не забывайте о собственном комфорте. Хорошо сядет на узкие бедра юбка-карандаш. Пусть она будет на завышенной талии или без пояса.
Верхняя одежда
Проблем с выбором не возникнет. Главное – не создать лишнюю массивность. Стройным колоннам огромное пространство вариантов предоставляет комфортный оверсайз. Поди угадай, что скрывается под эффектным и загадочным объемом. Полным не рекомендуется. Все прямоугольники могут воспользоваться общими правилами выбора:
- шубы – из короткого меха, прямые, А-силуэта, отрезные под кожаный пояс;
- пальто – трапеция, приталенные, с накладными карманами, с двубортной застежкой;
- плащи и жакеты в форме классического тренча;
- пуховики – баллоны, прямые без пояса;
- куртки – косухи, бомберы, пиджачного кроя.
Длина верхней одежды может быть любой. Зависит от собственного роста и предпочтений. Невысоким представительницам типа лучше не увлекаться фасонами в пол.
Невысоким представительницам типа лучше не увлекаться фасонами в пол.
Купальники
Лучшие купальники для фигуры прямоугольник – бикини.
- При маленькой груди выигрышно смотрится верх, отделанный бахромой, блестками, ярким принтом.
- Зрительно увеличивают бедра плавки-шортики, юбочки.
Крупная грудь требует надежного крепления. Благодаря этому, силуэт выглядит подтянутым.
Не увлекайтесь танкини и сплошными моделями. Если хочется закрытый вариант, подберите фасон с вырезами на талии, продольными или диагональными вставками, полосами, принтами. Нет отложений на боках – можете выбирать модель монокини.
Что необходимо исключить из гардероба
Имея представление о подходящей одежде, можно определить, что носить категорически нельзя или, по крайней мере, нежелательно. Табу распространяется на:
- узкие бретели;
- вырез горловины под шею;
- абсолютно прямые платья и юбки;
- сильно обтягивающую одежду из эластичных тканей;
- узкие ремни и пояса;
- рукава реглан, спущенную пройму;
- одновременно короткие топы и джинсы или шорты с низкой посадкой;
- брюки и юбки на кулисках;
- горизонтальные принты в средней части фигуры.

Старайтесь акцентировать четкую линию плеч, убирать все лишнее с талии и мягко ее обозначать или компенсировать недостаток изящества пышным подолом.
Обувь, аксессуары, украшения
Особых ограничений в выборе обуви нет. Стройные колонны могут носить балетки, сандалии, кеды, классические туфли, брутальные ботинки, элегантные ботильоны и сапоги. Полным прямоугольникам тоже ничего не возбраняется при наличии длинных ног. Невысоким лучше по минимуму использовать плоскую подошву и чаще выбирать средний или высокий каблук.
Сумка должна гармонировать по форме с очертаниями фигуры. Откажитесь от слишком романтических моделей в пользу классических, клатчей геометрической формы, мягких шопперов, рюкзаков. Следите, чтобы сумка находилась не в районе талии, а чуть выше или ниже.
Выбирайте эффектные серьги и броши. Носите длинные, цепи, бусы, свободно свисающие шарфы – все, что зрительно удлиняет силуэт. Мягкие пояса, в том числе из кожи, можно располагать где угодно.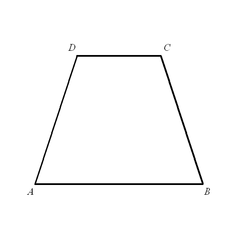 Широкие ремни, особенно с эффектными пряжками, носятся только на бедрах.
Широкие ремни, особенно с эффектными пряжками, носятся только на бедрах.
Фактура тканей и принтов
Прямоугольному типу не подходят тонкие эластичные и слишком грубые ткани. Выбирайте одежду из легких струящихся и достаточно плотных, но пластичных материалов:
- шифон;
- вискоза;
- шелк;
- накрахмаленный хлопок;
- вельвет;
- деним;
- габардин;
- шерсть;
- твид.
Избегайте косого кроя, струящиеся лини предательски выдадут все секреты. Не стоит бояться крупных принтов, наоборот, нежелательны мелкие. Рисунки и яркий декор должны располагаться ближе к лицу или в нижней части одежды.
Играйте на контрастах или создавайте монохромные комплекты. Высший класс – принты, формой создающие иллюзию талии. Эту же миссию выполняют строчки, драпировки, цветные вставки. Используйте эффект многослойности, и вы легко станете песочными часами.
Советы для поддержания формы
Девушки такого типа не могут пожаловаться на отсутствие аппетита и иногда набирают лишний вес, преимущественно в верхней или центральной части тела. В таких случаях силуэт становится похожим на перевернутый треугольник или яблоко. Можно воспользоваться рекомендациями в одежде для этих типов или похудеть.
В таких случаях силуэт становится похожим на перевернутый треугольник или яблоко. Можно воспользоваться рекомендациями в одежде для этих типов или похудеть.
Спортивное тело быстро откликается на физические нагрузки. Подойдут танцы, аэробика, плаванье, стретчинг, йога. Не увлекайтесь силовыми упражнениями. В вашем случае мышцы должны быть длинными и эластичными, а не короткими и накачанными.
От перекусов придется отказаться и держаться первую половину дня в относительно голодном состоянии. Ужин после 18 часов не только не вреден, он и рекомендован. Подходит спорное в плане полезности раздельное питание, но лучше придерживаться сбалансированного рациона.
Стиль от звезд-прямоугольников
Дизайнер, модельер, просто красивая женщина Виктория Бекхэм тоже прямоугольник. Черпайте вдохновение в ее творчестве и берите на заметку идеи у других знаменитостей. Подобным типом фигуры гордятся:
- Николь Кидман;
- Кэмерон Диаз;
- Мила Йовович;
- Кира Найтли;
- Пенелопа Крус;
- Ума Турман;
- Барбара Стрейзанд;
- Лайза Минелли;
- Тина Тернер.

У всех разные объемы, что в очередной раз подтверждает истину – красота не зависит от веса.
Геометрические фигурки и их названия. Удивительные фигуры в геометрии. Линейные геометрические фигуры
Геометрические фигуры представляют собой комплекс точек, линий, тел или поверхностей. Эти элементы могут располагаться как на плоскости, так и в пространстве, формируя конечное количество прямых.
Термин «фигура» подразумевает под собой несколько множеств точек. Они должны располагаться на одной или нескольких плоскостях и одновременно ограничиваться конкретным числом оконченных линий.
Основными геометрическими фигурами считаются точка и прямая. Они располагаются на плоскости. Кроме них, среди простых фигур выделяют луч, ломаную линию и отрезок.
Точка
Это одна из главных фигур геометрии. Она очень маленькая, но ее всегда используют для построения различных форм на плоскости. Точка — это основная фигура для абсолютно всех построений, даже самой высокой сложности. В геометрии ее принято обозначать буквой латинской алфавита, к примеру, A, B, K, L.
В геометрии ее принято обозначать буквой латинской алфавита, к примеру, A, B, K, L.
С точки зрения математики точка — это абстрактный пространственный объект, не обладающий такими характеристиками, как площадь, объем, но при этом остающийся фундаментальным понятием в геометрии. Этот нульмерный объект просто не имеет определения.
Прямая
Это фигура полностью размещается в одной плоскости. У прямой нет конкретного математического определения, так как она состоит из огромного количества точек, располагающихся на одной бесконечной линии, у которой нет предела и границ.
Существует еще и отрезок. Это тоже прямая, но она начинается и заканчивается с точки, а значит, имеет геометрические ограничения.
Также линия может превратиться в направленный луч. Такое происходит, когда прямая начинается с точки, но четкого окончания не имеет. Если же поставить точку посредине линии, то она разобьется на два луча (дополнительных), причем противоположно направленных друг к другу.
Несколько отрезков, которые последовательно соединяются друг с другом концами в общей точке и располагаются не на одной прямой, принято называть ломаной линией.
Угол
Геометрические фигуры, названия которых мы рассмотрели выше, считают ключевыми элементами, использующимися при построении более сложных моделей.
Угол — это конструкция, состоящая из вершины и двух лучей, которые выходят из нее. То есть стороны этой фигуры соединяются в одной точке.
Плоскость
Рассмотрим еще одно первичное понятие. Плоскость — это фигура, у которой нет ни конца, ни начала, равно как и прямой, и точки. Во время рассмотрения этого геометрического элемента во внимание берется лишь его часть, ограниченная контурами ломаной замкнутой линии.
Любую гладкую ограниченную поверхность можно считать плоскостью. Это может быть гладильная доска, лист бумаги или даже дверь.
Четырехугольники
Параллелограмм — это геометрическая фигура, противоположные стороны которой параллельны друг другу попарно. Среди частных видов этой конструкции выделяют ромб, прямоугольник и квадрат.
Среди частных видов этой конструкции выделяют ромб, прямоугольник и квадрат.
Прямоугольник — это параллелограмм, у которого все стороны соприкасаются под прямым углом.
Квадрат — это четырехугольник с равными сторонами и углами.
Ромб — это фигура, у которой все грани равны. При этом углы могут быть совершенно разными, но попарно. Каждый квадрат считается ромбом. Но в противоположном направлении это правило действует не всегда. Далеко не каждый ромб является квадратом.
Трапеция
Геометрические фигуры бывают совершенно разными и причудливыми. Каждая из них имеет своеобразную форму и свойства.
Трапеция — это фигура, которая чем-то схожа с четырехугольником. Она имеет две параллельные противоположные стороны и при этом считается криволинейной.
Круг
Эта геометрическая фигура подразумевает расположение на одной плоскости точек, равноудаленных от ее центра. При этом заданный ненулевой отрезок принято называть радиусом.
Треугольник
Это простая геометрическая фигура, которая очень часто встречается и изучается.
Треугольник считается подвидом многоугольника, расположенным на одной плоскости и ограниченным тремя гранями и тремя точками соприкосновения. Эти элементы попарно соединены между собой.
Многоугольник
Вершинами многоугольников называют точки, соединяющие отрезки. А последние, в свою очередь, принято считать сторонами.
Объемные геометрические фигуры
- призма;
- сфера;
- конус;
- цилиндр;
- пирамида;
Эти тела имеют нечто общее. Все они ограничиваются замкнутой поверхностью, внутри которой находится множество точек.
Объемные тела изучают не только в геометрии, но и в кристаллографии.
Любопытные факты
Наверняка вам будет интересно ознакомиться с информацией, предоставленной ниже.
- Геометрия сформировалась как наука еще в давние века. Это явление принято связывать с развитием искусства и разнообразных ремесел. А названия геометрических фигур свидетельствуют об использовании принципов определения подобия и схожести.

- В переводе с древнегреческого термин «трапеция» обозначает столик для трапезы.
- Если вы возьмете различные фигуры, периметр которых будет одинаковым, то наибольшая площадь гарантированно будет у круга.
- В переводе с греческого языка термин «конус» обозначает сосновую шишку.
- Существует известная картина Каземира Малевича, которая начиная с прошлого века притягивает к себе взгляды многих живописцев. Работа «Черный квадрат» всегда была мистической и загадочной. Геометрическая фигура на белом полотне восхищает и поражает одновременно.
Существует большое количество геометрических фигур. Все они отличаются параметрами, а порой даже удивляют формами.
Цели урока :
- Познавательная : создать условия для ознакомления с понятиями плоские и объёмные геометрические фигуры, расширить представление о видах объёмных фигур, научить определять вид фигуры, сравнивать фигуры.
- Коммуникативная : создать условия для формирования умения работать в парах, группах; воспитание доброжелательного отношения друг к другу; воспитывать у учащихся взаимопомощь, взаимовыручку.

- Регулятивная : создать условия для формирования планировать учебную задачу, выстраивать последовательность необходимых операций, корректировать свою деятельность.
- Личностная : создать условия для развития вычислительных навыков, логического мышления, интереса к математике, формирования познавательных интересов, интеллектуальных способностей учащихся, самостоятельность в приобретении новых знаний и практических умений.
Планируемые результаты:
личностные:
- формирование познавательных интересов, интеллектуальных способностей учащихся; формирование ценностных отношений друг к другу;
самостоятельность в приобретении новых знаний и практических умений; - формирование умений воспринимать, перерабатывать полученную информацию, выделять основное содержание.
метапредметные:
- овладение навыками самостоятельного приобретения новых знаний;
- организация учебной деятельности, планирования;
- развитие теоретического мышления на основе формирования умений устанавливать факты.

предметные:
- усвоить понятия плоские и объёмные фигуры, научиться сравнивать фигуры, находить плоские и объёмные фигуры в окружающей действительности, научиться работать с развёрткой.
УУД общенаучные :
- поиск и выделение необходимой информации;
- применение методов информационного поиска, осознанное и произвольное построение речевого высказывания в устной форме.
УУД личностные :
- оценивать свои и чужие поступки;
- проявление доверия, внимательности, доброжелательности;
- умение работать в паре;
- выражать положительное отношение к процессу познания.
Оборудование : учебник, интерактивная доска, смайлики, модели фигур, развёртки фигур, светофоры индивидуальные, прямоугольники -средства обратной связи, Толковый словарь.
Тип урока : изучение нового материала.
Методы : словесные, исследовательские, наглядные, практические.
Формы работы : фронтальная, групповая, парная, индивидуальная.
1. Организация начала урока.
Утром солнышко взошло.
Новый день нам принесло.
Сильными и добрыми
Новый день встречаем мы.
Вот мои руки, я раскрываю
Их навстречу солнцу.
Вот мои ноги, они твердо
Стоят на земле и ведут
Меня верной дорогой.
Вот моя душа, я раскрываю
Её навстречу людям.
Наступи, новый день!
Здравствуй, новый день!
2. Актуализация знаний.
Создадим хорошее настроение. Улыбнитесь мне и друг другу, садитесь!
Чтобы дойти до цели, надо прежде всего идти.
Перед вами высказывание, прочитайте. Что означает это высказывание?
(Чтобы чего-то добиться, нужно что-то делать)
И действительно, ребята, попадающим в цель может стать только тот, кто настраивает себя на собранность и организованность своих действий. И вот я надеюсь, что мы с вами на уроке достигнем своей цели.
Начнем наш путь к достижению цели сегодняшнего урока.
3. Подготовительная работа.
Посмотрите на экран. Что вы видите? (Геометрические фигуры)
Назовите эти фигуры.
Какое задание, вы можете предложить своим одноклассникам? (разделите фигуры на группы)
У вас на партах лежат карточки с этими фигурами. Выполните это задание в парах.
По какому признаку вы разделили эти фигуры?
- Плоские и объемные фигуры
- По основаниям объемных фигур
С какими фигурами мы уже работали? Что учились находить у них? Какие фигуры встречаются нам на геометрии впервые?
Какая же тема нашего урока? (Учитель добавляет слова на доске: объёмные, на доске появляется тема урока: Объёмные геометрические фигуры.)
Чему мы должны научиться на уроке?
4. «Открытие» нового знания в практической исследовательской работе.
(Учитель показывает куб и квадрат.)
Чем они похожи?
Можно ли сказать, что это одно и тоже?
Чем же отличается куб от квадрата?
Давайте проведём опыт. (Ученики получают индивидуальные фигуры – куб и квадрат.)
(Ученики получают индивидуальные фигуры – куб и квадрат.)
Попробуем приложить квадрат к плоской поверхности порты. Что видим? Он весь (целиком) лёг на поверхность парты? Вплотную?
! Как назовём фигуру, которую можно целиком расположить на одной плоской поверхности? (Плоской фигурой.)
Можно ли куб полностью (весь) прижать к парте? Проверим.
Можно ли назвать куб плоской фигурой? Почему? Есть ли пространство между рукой и партой?
! Значит, что мы можем сказать о кубе? (Занимает определённое пространство, является объёмной фигурой.)
ВЫВОДЫ: Чем же отличаются плоские и объёмные фигуры? (Учитель вывешивает на доске выводы.)
- Можно целиком расположить на одной плоской поверхности.
ОБЪЁМНЫЕ
- занимают определённое пространство,
- возвышаются над плоской поверхностью.
Объёмные фигуры: пирамида, куб, цилиндр, конус, шар, параллелепипед.
4. Открытие новых знаний.
1. Назовите фигуры, изображенные на рисунке.
Какую форму имеют основания этих фигур?
Какие еще формы можно увидеть на поверхности куба и призмы?
2. Фигуры и линии на поверхности объемных фигур имеют свои названия.
Предложите свои названия.
Боковые стороны, образующие плоскую фигуру называются гранями. А боковые линии – рёбра. Углы многоугольников – вершины. Это элементы объемных фигур.
Ребята, а как вы думаете, как называются такие объемные фигуры, у которых много граней? Многогранники.
Работа с тетрадями: чтение нового материала
Соотнесение реальных объектов и объёмных тел.
А теперь подберите для каждого предмета ту объёмную фигуру, на которую он похож.
Коробка – параллелепипед.
- Яблоко – шар.
- Пирамидка – пирамида.
- Банка – цилиндр.
- Горшок из-под цветка — конус.
- Колпачок – конус.
- Ваза – цилиндр.
- Мяч – шар.

5. Физминутка.
1. Представьте себе большой шар, погладьте его со всех сторон. Он большой, гладкий.
(Ученики «обхватывают» руками и гладят воображаемый шар.)
А теперь представьте себе конус, дотроньтесь до его вершины. Конус растёт вверх, вот он уже выше вас. Допрыгните до его вершины.
Представьте, что вы внутри цилиндра, похлопайте по его верхнему основанию, потопайте по нижнему, а теперь руками по боковой поверхности.
Цилиндр стал маленькой подарочной коробочкой. Представьте, что вы сюрприз, который находится в этой коробочке. Я нажимаю кнопку и… сюрприз выскакивает из коробочки!
6. Групповая работа :
(Каждая группа получает одну из фигур: куб, пирамиду, параллелепипед.Полученную фигуру дети изучают, выводы записывают в подготовленную учителем карточку .)
Группа 1. (Для изучения параллелепипеда)
Группа 2. (Для изучения пирамиды)
Группа 3. (Для изучения куба)
7. Решение кроссворда
Решение кроссворда
8. Итог урока. Рефлексия деятельности.
Решение кроссворда в презентации
Что нового вы для себя сегодня открыли?
Все геометрические фигуры можно разделить на объёмные и плоские.
А я узнал названия объёмных фигур
Геометрия — это раздел математики, в котором изучаются формы и их свойства.
Геометрия, которая изучается в школе, называется евклидовой, по имени древнегреческого учёного Евклида (III век до н. э.).
Изучение геометрии начинается с планиметрии. Планиметрия — это раздел геометрии, в котором изучаются фигуры, все части которых находятся в одной плоскости.
Геометрические фигуры
В окружающем нас мире существует множество материальных предметов разных форм и размеров: жилые дома, детали машин, книги, украшения, игрушки и т. д.
В геометрии вместо слова предмет говорят геометрическая фигура. Геометрическая фигура (или кратко: фигура ) — это мысленный образ реального предмета, в котором сохраняются только форма и размеры, и только они принимаются во внимание.
Геометрические фигуры разделяют на плоские и пространственные . В планиметрии рассматриваются только плоские фигуры. Плоской геометрической фигурой называется такая, все точки которой лежат на одной плоскости. Представление о такой фигуре даёт любой рисунок, сделанный на листе бумаги.
Геометрические фигуры бывают весьма разнообразны, например, треугольник, квадрат, окружность и др.:
Часть любой геометрической фигуры (кроме точки), также является геометрической фигурой. Объединение нескольких геометрических фигур, тоже будет являться геометрической фигурой. На рисунке ниже левая фигура состоит из квадрата и четырёх треугольников, а правая фигура состоит из окружности и частей окружности.
Раиса Баландина
«Объемные геометрические фигуры»
Конспект НОД в подготовительной группе на тему :
«Объемные геометрические фигуры » .
Задачи :
Упражнять в счёте в пределах 20 в прямом и обратном порядке
Закрепить знания о последовательности дней недели, времён года
Закрепить представления детей о геометрических фигурах
НОД занятия.
Ребята, посмотрите, сегодня утром я шла в детский сад и встретила почтальона. Он мне дал вот такое интересное письмо. Его прислал Буратино. Он уже ходит в школу. Вот,что он пишет :
«Дорогие ребята! Для того чтобы хорошо учиться в школе, надо много знать, уметь, думать, догадываться. А также решать необычные задачи, выполнять задания на смекалку и сообразительность. Вот мне и задали такие задания, а я затрудняюсь их выполнить. Помогите мне, пожалуйста».
Ребята, давайте поможем Буратино.
1 задание.Ответьте на вопросы :
Какое время года сейчас? (Весна)
Назовите весенние месяцы
Какой месяц сейчас идёт? (март)
Сколько дней в недели? (семь)
Назови их;
Какой сегодня день недели? (вторник)
Какой четверг по счету? (четвертый)
Вчера какой был день недели?
Завтра какой будет день недели?
2 задание.
Ребята, Буратино, не может выполнить следующее задание. Давайте ему поможем :
Давайте ему поможем :
Какой бывает счет? (прямой и обратный)
Считай от 10 до 20;
Считай от 20 обратно;
Назови число меньше пятнадцати;
Назови соседа 11 и 14;
Сравни числа 16 и 18;
Сравни числа 15 и 15;
3 задание.
Воспитатель : А сейчас мы будем работать с карточкой, которую прислал Буратино. Вы должны рассказать, где и как расположены фигуры .
Воспитатель : — Где находиться прямоугольник?
Ребенок : — Прямоугольник находится посередине.
Воспитатель : — Где находится овал?
Ребенок : — Овал находится справа от прямоугольника
Воспитатель : — Где находится круг?
Ребенок : — Круг находится внизу, под прямоугольником
Воспитатель : — Где находится квадрат?
Ребенок : — Квадрат находится слева от прямоугольника
Воспитатель : — Где находится треугольник?
Ребенок : — Треугольник находится сверху, над прямоугольником.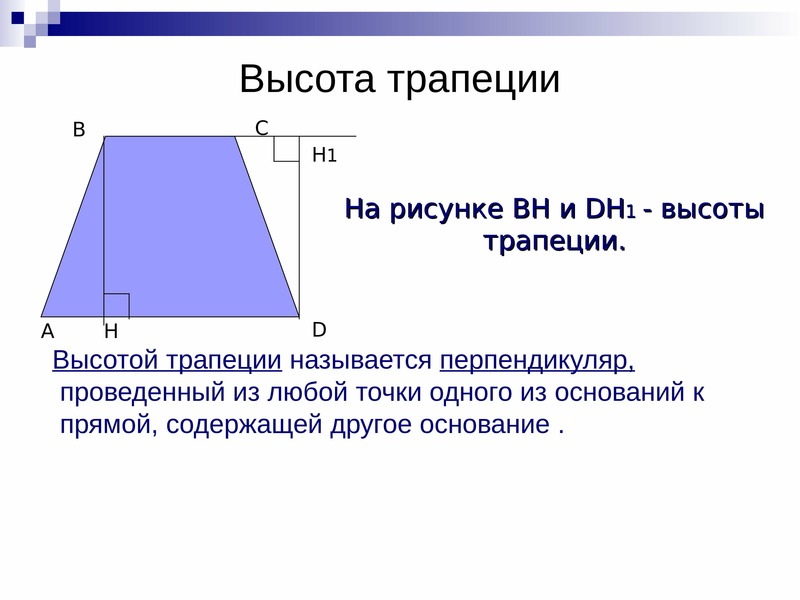
Физминутка.
Поработали, ребятки,
А теперь все на зарядку!
Столько раз ногою топнем (показываю цифру 6)
Столько раз руками хлопнем (показываю цифру 10)
Мы присядем столько раз (показываю цифру 7)
Мы наклонимся сейчас (показываю цифру 4)
Мы подпрыгнем ровно столько (показываю цифру 8)
Ай да счёт! Игра и только.
4 задание.
На столе перед детьми расположены объёмные геометрические фигуры (шар, куб, цилиндр, конус)
— Следующее задание : Дети что это? Какие фигуры ? Сколько их? Какая фигура стоит первой ? Второй? Третьей? Какая стоит последней?
Воспитатель : Ребята, а вы знаете, что геометрические фигуры можно нарисовать , начертить в тетради, вырезать из цветной бумаги. А еще их можно выложить из счетных палочек. И не одну, а сразу несколько. Давайте попробуем.
А)- отсчитайте три палочки и сделайте треугольник
Отсчитайте еще две палочки и сделайте еще один треугольник
Сколько треугольников получилось? (два)
Сколько палочек вы отсчитали?
Б)- отсчитайте четыре палочки и сделайте квадрат.
Отсчитайте еще три палочки и сделайте еще один квадрат
Какая фигура у вас получилась ? (прямоугольник)
Сколько четырехугольников получилось? (три)
А сколько многоугольников получилось? (три)
Назовите их (два квадрата и один многоугольник)
На какие делятся геометрические фигуры ? (объёмные и плоские)
Чем они отличаются друг от друга? (плоские можно расположить на плоскости, а объёмные нет) .
Мы сейчас с вами выкладывали на столе объемные или плоские фигуры ?
А сейчас мы с вами сделаем из палочек и пластилина фигуру , которая состоит из нескольких… а чего? Вы узнаете,отгадав загадку :
Три вершины в нем видны,
Три угла, три стороны,
С ним знаком даже дошкольник
Ведь фигура – (треугольник) .
Ребята, как называется фигура , которая состоит из нескольких треугольников? (пирамида)
Давайте, сделаем из пластилина и счетных палочек пирамиду.
5 задание.
Ребята, Буратино говорит, что вы уже устали — давайте поиграем. Эта игра — испытание «Верно-неверно» — поможем исправить ошибки, которые Буратино специально кое-где оставил.
Если вы услышите то, что считаете правильным, хлопайте в ладоши, если же то, что не правильно – покачайте головой
Утром солнышко встает; (верно)
По утрам нужно делать зарядку; (верно)
Нельзя умываться по утрам; (неверно)
Днем ярко светит луна; (неверно)
Утром дети идут в детский сад; (верно)
Ночью люди обедают; (неверно)
Вечером вся семья собирается дома; (верно)
В неделе 7 дней; (верно)
За понедельником следует среда; (неверно)
После субботы идет воскресение; (верно)
Перед пятницей стоит четверг; (верно)
Всего 5 времен года; (неверно)
Весна наступает после лета; (неверно) .
8 задание. А теперь Буратино приготовил вам графический диктант. Вы должны нарисовать один из признаков (явлений весны) .
Дети, поставьте карандаш на выделенную точку и рисуйте по клеткам.
Посмотрите и сравните получившийся у вас рисунок с образцом.
Молодцы, ребята!
Итог занятия.
Вот и выполнили вы все задания Буратино. Что же мы сегодня нового узнали? Какие задания с вами выполняли? Какие задания были трудными?
Буратино благодарит вас за помощь.
Тема урока
Геометрические фигуры
Что такое геометрическая фигура
Геометрические фигуры – это совокупность множества точек, линий, поверхностей или тел, которые расположены на поверхности, плоскости или пространстве и формирует конечное количество линий.
Термин «фигура» в какой-то степени формально применяется к множеству точек, но как правило фигурой принято называть такие множества, которые расположенные на плоскости и ограничиваются конечным числом линий.
Точка и прямая — это основные геометрические фигуры, расположенные на плоскости.
К самым простым геометрическим фигурам на плоскости принадлежат — отрезок, луч и ломаная линия.
Что такое геометрия
Геометрия – это такая математическая наука, которая занимается изучением свойств геометрических фигур. Если дословно перевести на русский язык термин «геометрия», то он обозначает «землемерие», так как в стародавние времена основной задачей геометрии, как науки, стало измерение расстояний и площадей на поверхности земли.
Практическое применение геометрии бесценно во все времена и независимо от профессии. Без знаний геометрии не может обойтись ни рабочий, ни инженер, ни архитектор и даже художник.
В геометрии есть такой раздел, который занимается изучением различных фигур на плоскости и называется планиметрия.
Вам уже известно, что фигурой называют произвольное множество точек, находящиеся на плоскости.
К геометрическим фигурам принадлежат: точка, прямая, отрезок, луч, треугольник, квадрат, круг и другие фигуры, которые изучает планиметрия.
Точка
Из выше изученного материала вам уже известно, что точка относится к главным геометрическим фигурам. И хотя это самая малая геометрическая фигура, но она необходима для построения других фигур на плоскости, чертеже или изображении и является основой для всех остальных построений. Ведь построение более сложноватых геометрических фигур складывается из множества точек, характерных для данной фигуры.
В геометрии точки обозначают прописными буквами латинского алфавита, например, такими, как: А, В, С, D ….
А теперь подведем итог, и так, с математической точки зрения, точка является таким абстрактным объектом в пространстве, который не имеет объема, площади, длины и других характеристик, но остается одним из фундаментальных понятий в математике. Точка – это такой нульмерный объект, которые не имеет определения. По определению Евклида, точкой называют то, что невозможно определить.
Прямая
Как и точка, прямая относится к фигурам на плоскости, которая не имеет определения, так как состоит из бесконечного множества точек, находящихся на одной линии, которая не имеет ни начала ни конца. Можно утверждать, что прямая линия бесконечна и не имеет предела.
Если же прямая начинается и заканчивается точкой, то она уже не является прямой и называется отрезком.
Но иногда прямая, с одной стороны имеет точку, а с другой нет. В таком случае прямая превращается в луч.
Если же взять прямую и на ее средине поставить точку, то она разобьет прямую на два противоположно направленных луча. Данные лучи являются дополнительными.
Если же перед вами несколько отрезков, соединенных между собой так, что конец первого отрезка становиться началом второго, а конец второго отрезка — началом третьего и т. д., и эти отрезки находятся не на одной прямой и при соединении имеют общую точку, то такая цепочка является ломаной линией.
Задание
Какая ломаная линия называется незамкнутой?
Как обозначается прямая?
Как называется ломаная линия, у которой четыре замкнутых звена?
Какое название имеет ломаная линия с тремя замкнутыми звеньями?
Когда конец последнего отрезка ломаной совпадает с началом 1-го отрезка, то такую ломаную линию называют замкнутой. Примером замкнутой ломаной является любой многоугольник.
Плоскость
Как точка и прямая, так и плоскость является первичным понятием, не имеет определения и у нее нельзя увидеть ни начала, ни конца. Поэтому, при рассмотрении плоскости, мы рассматриваем только ту ее часть, которая ограничивается замкнутой ломаной линией. Таким образом, плоскостью можно считать любую гладкую поверхность. Этой поверхностью может быть лист бумаги или стола.
Угол
Фигура, которая имеет два луча и вершину, называется углом. Место соединения лучей, является вершиной этого угла, а его сторонами считаются лучи, которые этот угол образуют.
Задание:
1. Как в тексте обозначают угол?
2. Какими единицами можно измерить угол?
3. Какие бывают углы?
Параллелограмм
Параллелограмм — это четырехугольник, противолежащие стороны которого попарно параллельны.
Прямоугольник, квадрат и ромб являются частными случаями параллелограмма.
Параллелограмм, имеющий прямые углы равные 90 градусам, является прямоугольником.
Квадрат — это тот же параллелограмм, у него и углы и стороны равны.
Что до определения ромба, то это такая геометрическая фигура, все стороны которого равны.
Кроме того, следует знать, что любой квадрат является ромбом, но не каждый ромб может быть квадратом.
Трапеция
При рассмотрении такой геометрической фигуры, как трапеция, можно сказать, что в частности она, как и четырехугольник имеет одну пару параллельных противолежащих сторон и является криволинейной.
Окружность и круг
Окружность — геометрическое место точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое её радиусом.
Треугольник
Также к простым геометрическим фигурам принадлежит и уже изучаемый вами треугольник. Это один из видов многоугольников, у которого часть плоскости ограничена тремя точками и тремя отрезками, которые соединяют эти точки попарно. Любой треугольник имеет три вершины и три стороны.
Задание: Какой треугольник называют вырожденным?
Многоугольник
К многоугольникам относятся геометрические фигуры разных форм, у которых замкнутая ломаная линия.
В многоугольнике все точки, которые соединяют отрезки, являются его вершинами. А отрезки, из которых состоит многоугольник, являются его сторонами.
А известно ли вам, что возникновение геометрии уходит в глубину веков и связано с развитием различных ремесел, культуры, искусства и наблюдением за окружающим миром. Да и название геометрических фигур является тому подтверждением, так как их термины, возникли не просто так, а благодаря своей схожести и подобию.
Ведь термин «трапеция» в переводе с древнегреческого языка от слова «трапезион» обозначает столик, трапеза и другие производные слова.
«Конус» произошел от греческого слова «конос», что в переводе звучит, как сосновая шишка.
«Линия» имеет латинские корни и происходит от слова «линум», в переводе это звучит, как льняная нить.
А знаете ли вы, что если взять геометрические фигуры с одинаковым периметром, то среди них обладателем самой большой площади оказался круг.
ОСНОВЫ КОМПОЗИЦИИ: Геометрия в фотографии
09 Февраля 2016
Фотография — это то, чем становятся живопись, композиция, пластический ритм, геометрия, размещенные в считанных долях секунды (Анри Картье-Брессон).
Фото: Ronald Koster
Когда мы думаем о композиции в фотографии, первое, что приходит в голову — это золотое сечение, правило третей, формат кадра, контраст, точка съемки…
Но есть еще один важный элемент в композиции – геометрия. Геометрия в фотографии — это простые формы, такие как квадрат, треугольник, круг, прямые и кривые линии.
Геометрические объекты обычно вспомогательные, они усиливают восприятие и могут объединять отдельные элементы фотографии в единое целое. Выбирая ту или иную геометрическую форму в фотографии, автор может заранее акцентировать внимание будущего зрителя на его определенных зонах. Установлено, например, что углы квадрата оказываются очень активными зонами, а для круга или овала – это центр. Не случайно, с давних времен сложилась традиция портретов в овале. Углы не отвлекали внимание от главного — изображения лица. Наиболее распространенный и наиболее разносторонний геометрический инструмент – это линии. Более подробно о них читайте в нашей отдельной статье.
Фактически, любой объект окружающей среды можно сравнить с какой-либо геометрической фигурой, но все они пробуждают у зрителя разные эмоции и чувства. Простые геометрические формы, такие как круг и квадрат, намного быстрее фиксируются нашим глазом и воспринимаются мозгом, а следовательно и лучше запоминаются, нежели сложные и неправильные. Вообще выделяют три базовых фигуры. Это прямоугольник, треугольник и круг. Всё остальное – овал, квадрат, трапеция, эллипс, ромб всего лишь их вариации. Все они отличаются как графически, так и (не удивляйтесь) эмоционально.
КВАДРАТ В КОМПОЗИЦИИ
Квадрат — это самая устойчивая, законченная форма, готовая вызывать утверждающие образы. Он ассоциируется с такими понятиями, как порядок, стабильность, надежность, прочность. В то же время, квадрат воспринимается несколько приземленно и тяжеловесно.
Фото: Robertino Nikolic. “Свет играет с геометрией или геометрия со светом?”. Победитель конкурса Black & White Spider Awards, 2007.
Фото: Alma (источник — 1510.deviantart.com)
Фото: G. Diaz Deleon
ПРЯМОУГОЛЬНИК В КОМПОЗИЦИИ
Прямоугольник, расположенный̆ большей̆ стороной̆ по горизонтали вызывает ощущение стабильности, покоя, основательности.
Фото: Guerel Sahin
Фото: Guerel Sahin
Особенно гармонично смотрится, если он выполнен в пропорциях «золотого сечения». Прямоугольник, расположенный̆ большей̆ стороной̆ вдоль вертикали, создаёт ощущение лёгкости, воздушности.
Фото: Joe McNally
ТРЕУГОЛЬНИК В КОМПОЗИЦИИ
Треугольник — наиболее часто встречающаяся в природе форма. Треугольник — самая динамичная, неустойчивая форма, которая ассоциируется с движением, развитием, скоростью. В положении «вершиной вверх» вызывает образы устойчивости, стабильности (пирамида). Несколько треугольников — позитивное динамическое движение. В положении «вершиной вниз» – шаткое равновесие, балансировка. В отличие от прямоугольника, стороны не противостоят друг другу, а меняют направление развития. Это может быть использовано для создания конкретных образов. Треугольник естественным образом вносит в композицию ощущение глубины пространства.
Фото: Josh Johnson
КРУГ В КОМПОЗИЦИИ
В форме круга более чем, в какой̆ — либо, выражена идея природы, земли, мироздания. Круги изобилуют как в природе, так и в мире рукотворных предметов. Поэтому такие понятия как «добро», «жизнь», «счастье», «процветание» ассоциируются у человека именно с этой̆ формой̆. Данная форма направляет взгляд внутрь кадра. Круг ассоциируется с чем-то легким, воздушным и при этом – уравновешенным. Но, в отличие от квадрата, это равновесие ближе к физическому понятию «неустойчивое равновесие». Круги — самые приятные глазу фигуры, которые можно смело использовать в кадре. Они сразу приковывают внимание зрителя и, благодаря своей идеальной симметричности, привносят в изображение гармонию. Поскольку у круга нет углов, он прекрасно контрастирует с прямоугольным обрезом кадра.
Фото: Steve McCurry
Фото: Georgios Karamanis
Фото: Elia Locardi
Как и треугольник, круг — очень эффектная геометрическая фигура, которую можно с пользой применить в композиции кадра, хотя и с другим смыслом. В отличие от диагоналей, заряжающих кадр динамикой и напряжением, кривые линии создают гармонию. Таким образом, можно создавать выразительные и информативные композиции, основанные на простых геометрических фигурах.
Фото: William Morris Kahn
Фото: Joe McNally
Фото: Joe McNally
Геометрические объекты можно условно разделить на три группы по их функциям: направляющие линии, разделители пространства и обрамление. Разделители пространства делят снимок на отдельные зоны, несущие свою смысловую нагрузку, но работающие вместе для создания единой композиции. Примером, простейшего разделителя пространства может послужить линия горизонта, отделяющая небо от поверхности моря. Очень хорошо смотрятся в качестве разделителя пространства треугольники, но и такие элементы, как диагонали и незамкнутые линии, тоже уверенно можно использовать.
Фото: Вадим Докторов
Обрамления носят функцию притяжения взгляда зрителя и его фокусировку на основном объекте. В качестве обрамляющих элементов отлично работают дверные проемы, арки, окна. Кроме того, великолепно с этой функцией справляются и естественные элементы, например, ветви деревьев. Важно чтобы обрамление присутствовало, как минимум, с двух сторон снимка и было выполнено в спокойной тональности, желательно более темной, чем главный объект, чтобы не отвлекать зрителя. Обрамляющий элемент должен иметь интересный цвет, форму, текстуру или иные примечательные характеристики, но стоит помнить, что обрамляющие элементы должны направлять, а не отвлекать. Особенно хорошо в этом плане работают треугольники или арки. Арка способна создать интересную динамичную композицию.
Фото: Guerel Sahin
Фото: Ian Plant
Фото: Tom La
Пробуйте, экспериментируйте и не забывайте, что в одном снимке вы можете использовать сразу несколько геометричских фигур для построения композиции.
Другие статьи о композиции в фотографии:
Золотое сечение в фотографии
Сила линий в фотографии
Формат кадра в фотографии
Контраст в фотографии (Часть 1)
Контраст в фотографии (Часть 2)
Точка съемки и выбор плана
Ракурс
Равновесие в композиции
Геометрические фигуры: картинки для детей
В этом разделе моего блога Вы можете скачать картинки и раскраски геометрических фигур для детей. Ваш ребенок познакомится с такими геометрическими фигурами, как: квадрат, круг, прямоугольник, равнобедренный треугольник, пятиугольник, шестиугольник, восьмиугольник, сердце, овал, звезда, прямоугольный треугольник, ромб, воздушный змей или кайт, крест и полукруг, а также объемные фигуры, например, цилиндр.
Пособия и материалы по теме
Все геометрические фигуры для детей, их картинки, рисунки или раскраски Вы можете разрезать на отдельные карточки и изучать вместе с Вашим ребенком. Из них может получиться отличная аппликация.
Все представленные плоские и объемные фигуры для дошкольников разноцветные и яркие, с ними будет приятно играть и познавать любому малышу.
Картинки, рисунки и раскраски геометрических фигур для малышей предназначены как для индивидуального использования, так и для групповых занятий в школах раннего развития и детских садах.
Занятия с карточками геометрических фигур развивают кругозор Вашего малыша, позволяют узнать название и виды различных фигур.
Разнообразьте свои занятия для детей различными играми с карточками геометрических фигур, например,
- можно искать похожие на эти геометрические фигуры предметы в доме,
- распечатать два варианта с геометрическими фигурами, один вариант разрезать на карточки и прикладывать к другому,
- можно также просто распечатать геометрические фигуры для дошкольников, разрезать на карточки и развесить по комнатам на уровне глаз ребенка. Иногда подходить к карточкам и ненавязчиво называть геометрические фигуры, а потом, когда почувствуете, что малыш усвоил информацию, спрашивать его.
Придумайте и Вы свои варианты игры.
Скачать и распечатать геометрические фигуры в картинках Вы можете здесь совершенно бесплатно — нажмите на картинку ниже.
Геометрически фигуры с названиями на русском языке.Названия на английском языке. Задание: соедини линией одинаковые по форме геометрические фигуры. Назови и напиши названия всех геометрических фигур.Соедини линией одинаковые по форме геометрические фигуры.Обведи пунктирные линии.Посчитай, сколько геометрических фигурПострой логическую цепочку.Найди все квадраты и раскрась.
Разрежь на части фигуры и назови их.Раскрась в соответсвующие цвета.Обведи и назови. Посчитай, сколько на рыбке фигур?
Аппликация
Интересным видом работы для детей может стать аппликация. Вы можете вырезать круг или квадрат, а затем попросить малыша наклеить его на основу. Такие фигуры, как квадрат, овал, круг могут стать основой для небольшой картинки.
Интересно будет склеить из бумаги объемные фигуры, например, параллелепипед или цилиндр. Правда, для этого понадобится плотный картон, зато дети узнают, что в основе параллелограмма лежит квадрат, а в цилиндр берет за основу круг. Аппликация поможет развивать творческие способности детей. Цилиндр или параллелограмм можно впоследствии использовать как коробочку для небольших игрушек.
Материалы для скачивания
Шаблоны животных из геометрических фигур Вы можете скачать здесь.
Вырежи и склей домик.Эти геометрические фигуры Вы можете вырезать и придумать свои аппликации. Сделай веселый квадрат из бумаги. Вырежи и приклей окна к домику.Аппликация для дошкольников, как и раскраски, развивает мелкую моторику пальцев, стимулирует центры речи. Занимайтесь со своим малышом: изучайте геометрические фигуры!
Видео
Гардероб по типу фигуры: фото и рекомендации
Одежда для типа фигуры:
Мало кого из женщин нашей планеты природа наградила сразу и ногами «от ушей», и осиной талией, и грудью 5-того размера. Как же быть тем, кто мечтает выглядеть по-королевски, а внешние данные до идеальных явно не дотягивают?
Шикарная фигура на самом деле — не такой уж и неотъемлемый признак «женщины-королевы», гораздо важнее уметь скрыть свои недостатки и подчеркнуть имеющиеся достоинства. Сделать это можно с помощью правильно подобранной одежды. Прежде чем отправляться за обновками в магазин, определите, к какому типу телосложения относится ваша фигура. Итак, выбираем гардероб по типу фигуры.
Все фигуры условно разделяют на 4 типа: трапеция (груша), треугольник, прямоугольник и песочные часы. Иногда добавляют яблоко (округлый вариант прямоугольника).
Одежда для женщин с типом фигуры трапеция (груша)
У женщины с фигурой-трапецией обычно четкая талия и бедра шире плеч. С такой фигурой ни в коем случае нельзя носить облегающие вещи, лучше всего в этом случае будет смотреться полуприлегающая одежда.
Если у вас красивые ноги, очень хорошо подойдут вам слегка расширяющиеся к подолу юбки или брюки, скроенные прямо и зауженные внизу. Такие вещи отвлекут внимание от излишне широких бедер и, наоборот, притянут взгляды к стройным ножкам.
Зрительно уменьшить бедра поможет и выбор цвета одежды.
Если мы выбираем гардероб по типу фигуры «трапеция», стоит отдавать предпочтение темным черным или коричневым оттенкам брюк, джинсов и юбок и однотонным пастельным – блузок, свитеров и кофточек. Выбирая платье, стоит остановиться на том варианте, который выгодно подчеркнет грудь.
Слегка приталенное платье светло-зеленого, белого, голубого или сиреневого цветов придаст вашей фигуре практически идеальные пропорции.
Хороши для «груш» такие фасоны:
- — платье с полуприлегающим верхом и юбкой-солнце или полусолнце длиной до середины колена;
- — двухцветное платье с небольшой баской: верх светлый, низ темный;
- — юбка-«рыбка» (приталенная, плотно обхватывающая бедра и мягко спускающаяся, расширяясь, до середины икры).
Женственным «грушам» стоит также обратить внимание на юбку-шорты. Эта модель настолько универсальна, что не только скроет лишние объемы «внизу», но и сделает ваш образ еще более притягательным за счет некоторой загадочности, неопределенности (не то юбка, не то шорты…).
Красиво смотрятся на «грушах» платья-футляры, платья с глубоким и широким вырезом, с пышным коротким рукавчиком. Вообще, «груши», помните: разнообразные платья – это ваш правильный выбор! А брюк и джинсов пусть будет немного поменьше в гардеробе.
Одежда для женщин с типом фигуры «перевернутый треугольник»
У фигуры-треугольника плечи, наоборот, шире бедер. Ее обладательницам стоит подчеркивать линию талии и делать акцент на красивых бедрах.
Придется отказаться от крупных орнаментов и рисунков, а также от горизонтальных полос на кофтах, джемперах и блузках.
- Жакеты лучше выбирать приталенные, с большими карманами и V-вырезом.
- Брюки и джинсы, в общем, подойдут любые. На такой фигуре будут выигрышно смотреться как раз светлые джинсы, особенно в сочетании с рубашками того же оттенка.
- Также светлыми должны быть и юбки, хорошо, если ткань будет в клетку или косую полоску. Длина юбок для «женщин-треугольников» может быть любая – чем краше ножки, тем короче юбка (естественно, в разумных пределах).
- «Треугольники» словно созданы для однотонных прямых платьев простого покроя. Лучше всего выбирать укороченные модели.
- Юбка-карандаш, которая хороша для любого возраста, способна придать шарм и элегантность даме с фигурой «перевернутый треугольник». Только нужно сбалансировать пропорции: например, выбрать юбку с накладными карманами или каким-нибудь ярким узором.
Как ни странно, модные сегодня платья с обтягивающим верхом и пышной-юбкой-«солнце» пойдут «треугольнику» не меньше, чем «груше». Но в данном случае верх должен быть именно четко облегающим фигуру. Кроме того, идеальный ворот для такого платья – закрытый. Хороши разнообразные воротнички-стойки, маленькие светлые воротнички «а ля гимназистка».
Прекрасно смотрятся на «треугольниках» платья-рубашки с тонким пояском.
Одежда для женщин с типом фигуры «Прямоугольник»
Женщины с фигурой-прямоугольником, как правило, имеют пропорциональные бедра и плечи при нечетко выраженной талии. Очень важно в таком случае для придания стройности очертить линию талии. Для этого стоит отдать предпочтение юбкам без пояса, брюкам-капри, жакетам прямого покроя и блузкам с небольшим рукавом.
Очень красиво на такой фигуре смотрятся платья на бретельках с прямым вырезом.
Когда выбираем гардероб по типу фигуры «прямоугольник», цвета в одежде можно в принципе использовать любые с условием, что и верх, и низ будут одного тона.
Аксессуары в виде разнообразных ремней лучше вообще исключить, они только подчеркнут недостатки, никак их не скрыв. Исключением может послужить широкий ремень контрастного цвета, не слишком плотно обхватывающий талию. Его роль в данном случае – «разделить» зрительно фигуру, «создать» линию талии, даже если фактически ее почти нет.
На ножках будет красиво смотреться обувь на невысоком каблуке или на платформе.
Хорошо сидят на «прямоугольниках» укороченные пиджаки, «косухи», джинсовые курточки.
Узкие джинсы и брюки смотрятся на такой фигурке гораздо лучше, чем на любой другой. Если вы обладаете такой фигурой, то можете смело позволить себе:
- — брюки скинни и топ с круглым вырезом;
- — леггинсы и свободный свитер;
- — ультракороткие шортики со свободной клетчатой блузкой.
«Мальчишеская» фигура дает возможность спокойно носить балетки (благодаря тому, что ноги у таких девушек обычно длинные и стройные, балетки не придадут образу тяжеловесность) или сапоги без каблука.
На холодное время года женщины с такой фигурой могут приобрести пальто в стиле «оверсайз» (то есть объемное) или полупальто длиной до бедер. Пиджачный крой будет просто великолепен в данном случае.
Одежда для типа фигуры «Яблоко»
«Яблоко» — в принципе, это одна из вариаций «прямоугольника». Женщины-«яблочки» тоже отличаются стройными ногами, прямыми плечами. Талия не выражена, присутствует лишь намек на нее. При этом они часто имеют полноватую грудь, слегка выдающийся животик, круглое лицо. Как одеться «яблоку»?
Сразу – о важном: детали, привлекающие внимание, сконцентрируйте наверху. Пусть это будут:
- — яркий шарфик;
- — крупная брошь;
- — красивые бусы.
Талию не акцентируем. Но можно использовать в некоторых моделях широкий жесткий пояс. Платья нужно подбирать полуприлегающие, желательно с рукавом. Хороши платья с запахом, с мягкими складочками в районе живота. Если вы решили надеть топ – пусть он будет снабжен квадратным декольте или каким-либо другим вырезом необычной, притягивающей взгляд формы.
«Яблоку» со стройными ногами не возбраняется мини. Интересно, что короткие юбки и шорты «сидят» на такой фигуре отлично почти в любом возрасте.
Хороши свободные брюки из мягких тканей. Выбираете купальник? Обратите внимание на танкини или цельный с вертикальными узорами.
Одежда для женщин с типом фигуры «Песочные часы»
Женщинам с фигурой «песочные часы» повезло больше всех – им пойдет любая одежда, лишь бы она не была бесформенной и безразмерной.
Брюки или джинсы лучше выбирать с заниженной талией, такие будут смотреться более выигрышно чем, к примеру, широкие брюки с высокой посадкой. Хотя и широкие брюки могут выглядеть на женщине-«песочных часах» очень эффектно, если надеть их, например, с белой блузкой и черным корсетом.
Дополнить образ можно любыми аксессуарами, бижутерией, высокими каблуками – позволяется практически все. Однако увлекаться тоже не стоит, красивая фигура – еще не повод навешивать на себя все доступные украшения.
Фигура «песочные часы» дает возможность экспериментировать. Кому-то больше пойдет маленькое черное платье «в облипку»; кто-то будет увереннее себя чувствовать в классическом офисном костюме; кто-то выберет ретро-стиль, а кого-то прельщает эпатажный стиль трэш.
Для «песочных часов» строгих запретов нет. Нужно ориентироваться главным образом на возраст, образ жизни и собственные предпочтения.
Природа наделила нас разными фигурами. Но каждая – прекрасна. Надо лишь научиться подчеркивать достоинства.
]]>Что такое трапеция? [Определение, факты и пример]
Что такое трапеция?
Трапеция, также известная как трапеция, представляет собой плоскую замкнутую форму, имеющую 4 прямые стороны с одной парой параллельных сторон.
Параллельные стороны трапеции называются основаниями, а непараллельные стороны — ножками. У трапеции тоже могут быть параллельные ножки. Параллельные стороны могут быть горизонтальными, вертикальными или наклонными.
Расстояние по перпендикуляру между параллельными сторонами называется высотой.
Примеры :
Без примеров :
Типы трапеций
Трапеция бывает трех типов, а именно
1. Правая трапеция : имеет пару прямых углов.
2. Равнобедренная трапеция : имеет одинаковую длину непараллельных сторон. На изображении стороны AD и BC равны.
3. Чешуйчатая трапеция : у нее нет равных углов и равных сторон.
Свойства трапеции
Трапеция называется параллелограммом, если обе пары ее противоположных сторон параллельны.
Трапеция — это квадрат, если обе пары его противоположных сторон параллельны; все его стороны равной длины и расположены под прямым углом друг к другу.
Трапеция может быть прямоугольником, если обе пары ее противоположных сторон параллельны; его противоположные стороны равны по длине и расположены под прямым углом друг к другу.
Примеры из реальной жизни
Некоторые из многих примеров трапеции — это лицевая сторона коробки для попкорна, сумочки и мостов.
Интересные факты
|
Трапеция
(Перейти к области трапеции или периметру трапеции)
Трапеция — это четырехсторонняя плоская форма с прямыми сторонами, имеющая пару противоположных сторон, параллельных (отмечены стрелками ниже):
| Трапеция | Равнобедренная трапеция |
Трапеция:
| имеет пару параллельных сторон | |
— это равнобедренная трапеция , когда она имеет равных углов с параллельной стороны | |
| в Великобритании называется «трапеция » (см. Ниже) |
Люфт трапецией:
Параллельные стороны — это «основания»
Две другие стороны — «ножки»
Расстояние (под прямым углом) от одной базы до другой называется «высотой»
Площадь трапеции
Площадь — это среднее значение двух базовых длин, в раз превышающее высоту : Площадь = a + b 2 × h |
Пример: два основания трапеции составляют 6 м и 4 м, а высота — 3 м.Какова его площадь?
Площадь = 6 м + 4 м 2 × 3 м = 5 м × 3 м = 15 м 2
Инструмент «Площадь многоугольника путем рисования» полезен, когда вы можете нарисовать трапецию.
Периметр трапеции
Периметр — это расстояние по краям.
Периметр равен сумме длин всех сторон : Периметр = a + b + c + d |
Пример: Трапеция имеет длину стороны 5 см, 12 см, 4 см и 15 см. Каков ее периметр?
Периметр = 5 см + 12 см + 4 см + 15 см = 36 см
Медиана трапеции
Медиана (также называемая средней линией или срединным сегментом) — это линейный сегмент на полпути между двумя основаниями. Средняя длина — это среднее значение двух базовых длин: м = а + б 2 |
Вы можете рассчитать площадь, зная медианное значение, это просто медиана, умноженная на высоту:
Площадь = mh
Трапеция
A trapezium (UK: trapezoid) — четырехугольник без параллельных сторон.
Определения США и Великобритании поменялись местами, например:
| Трапеция | Трапеция | |
| США: | Пара параллельных сторон | НЕТ параллельных сторон |
| Великобритания: | НЕТ параллельных сторон | Пара параллельных сторон |
Как рассчитать площадь неправильной трапеции
Обновлено 22 декабря 2020 г.
Эллиот Уолш
Хотя может показаться, что определение площади различных форм и многоугольников ограничено школьным математическим классом, факт остается фактом: определение площади полигонов — это то, что применимо практически ко всем сферам жизни.От сельскохозяйственных расчетов до понимания области определенной экосистемы, от биологии до информатики, расчет областей сложной формы — важный навык, который необходимо освоить.
Обычно проще измерить площадь фигур со всеми равными сторонами и простыми формулами. Однако «неправильные» формы, такие как неправильная трапеция, также известная как неправильная трапеция, обычны и также должны быть рассчитаны. К счастью, существуют калькуляторы площади неправильной трапеции и формула площади трапеции, которая упрощает процесс.
Что такое трапеция?
Трапеция — это четырехсторонний многоугольник, также известный как четырехугольник, который имеет как минимум один набор параллельных сторон . Это отличает трапецию от параллелограмма, поскольку параллелограммы всегда имеют двух наборов параллельных сторон. Вот почему вы можете считать все параллелограммы трапециями, но не все трапеции параллелограммами.
Параллельные стороны трапеции называются основаниями , а непараллельные стороны трапеции называются опорами .Правильная трапеция, также называемая равнобедренной трапецией, представляет собой трапецию, у которой непараллельные стороны (ноги) равны по длине.
Что такое неправильная трапеция?
Неправильная трапеция, также называемая неправильной трапецией, — это трапеция, у которой непараллельные стороны не равны по длине. То есть у них ноги двух разной длины.
Формула площади трапеции
Чтобы найти площадь трапеции, вы можете использовать следующее уравнение:
\ text {Area} = \ bigg (\ frac {b_1 + b_2} {2} \ bigg) × h
b 1 и b 2 — длины двух оснований трапеции; h равно высоте трапеции, которая является длиной от нижнего основания до верхней базовой линии.
Вы не всегда учитываете высоту трапеции. В таком случае высоту часто можно вычислить с помощью теоремы Пифагора.
Как рассчитать площадь неправильной трапеции: заданные значения
Этот первый пример представляет проблему, когда вы знаете все значения трапеции.
b_1 = 4 \ text {cm} \\ b_2 = 12 \ text {cm} \\ h = 8 \ text {cm}
Просто вставьте числа в формулу площади трапеции и решите.2 \ end {align}
Как рассчитать площадь неправильной трапеции: определение высоты неправильной трапеции
В других проблемах или ситуациях с неправильными трапециями вам часто дают только размеры оснований и опоры трапеции вместе с некоторыми углами трапеции, что позволяет вам рассчитать высоту самостоятельно, прежде чем вы сможете рассчитать площадь.
Затем вы можете использовать длину и углы, чтобы вычислить высоту трапеции, используя общие правила треугольного угла.
Подумайте об этом. . . когда вы рисуете линию высоты на трапеции в конечной точке от меньшей базовой длины до более длинной базовой длины, вы создаете треугольник с этой линией в качестве одной стороны, катетом трапеции как второй стороной и расстоянием от точка, в которой линия высот касается большего основания, до точки, где это основание встречается с ногой в качестве третьей стороны (см. подробное изображение здесь).
Допустим, у вас есть следующие значения (см. Изображение на этой странице):
b_1 = 16 \ text {cm} \\ b_2 = 25 \ text {cm} \\ \ text {leg} 2 = 12 \ text { cm} \\ \ text {Угол между} b_2 \ text {и ногой} 2 = 30 \ text {градусов}
Знание углов и одного из значений длины стороны означает, что вы можете затем использовать правила sin и cos, чтобы найти рост.Гипотенуза будет равна катету 2 (12 см), и у нас есть углы для вычисления высоты.
Давайте используем sin, чтобы найти высоту, используя заданный угол 30 градусов, что сделает высоту равной «противоположной» в уравнении sin:
\ sin (\ text {angle}) = \ frac {\ text {height }} {\ text {hypotenuse}} \\ \, \\ \ sin (30) = \ frac {\ text {height}} {12 \ text {cm}} \\ \, \\ \ sin (30) × 12 \ text {cm} = \ text {height} = 6 \ text {cm}
Теперь, когда у вас есть значение высоты, вы можете вычислить площадь, используя формулу площади:
\ begin {align} A & = \ bigg (\ frac {b_1 + b_2} {2} \ bigg) × h \\ & = \ bigg (\ frac {b_1 + b_2} {2} \ bigg) × h \\ & = \ bigg (\ frac {16 \ text {cm} + 25 \ text {cm}} {2} \ bigg) × 6 \ text {cm} \\ & = \ bigg (\ frac {41 \ text {cm}} {2} \ bigg) × 6 \ текст {см} \\ & = 20.2 \ end {align}
Основания трапеции, ножки, углы и площадь, правила и формулы
Трапеция — это четырехугольник с одной парой параллельных линий
Основания — две параллельные линии называются основаниями.
Ноги — две непараллельные линии — это ноги.
Недвижимость- Свойство №1) Углы на одной стороне ножки называются смежными углами и являются дополнительными (еще )
- Свойство № 2) Площадь трапеции = $$ Площадь = высота \ cdot \ left (\ frac {\ text {sum base}} {2} \ right) $$ (еще )
- Объект № 3) Трапеции имеют средний сегмент, соединяющий вершины ног (еще )
Смежные углы трапеции
Углы на одной стороне ножки называются смежными углами, например $$ \ angle A $$ и $$ \ angle D $$ являются дополнительными.По той же причине $$ \ angle B $$ и $$ \ angle C $$ являются дополнительными.
Задача 1
$$ \ angle ZWX = 180 — 44 = 136 ° $$
Проблема 2
Используйте теорему о смежных углах для вычисления m $$ \ angle MLO $$.
Показать ответ$$ \ angle MLO = 180-124 = 56 ° $$
Проблема 3
Найдите значение x на трапеции ниже, затем определите меру углов $$ \ angle WXY $$ и $$ \ angle XYZ $$.
Показать ответПроблема 4
Что не так с трапецией LMNO, изображенной ниже? (Объясните, почему LMNO не может быть трапецией, основываясь на предоставленной информации) .
Показать ответЕсли LMNO представляет собой трапецию и ее основания LO и MN параллельны, тогда $$ \ angle MNO $$ и $$ \ angle NOL $$, которые должны быть дополнительными, сумма этих углов не равна 180 111 + 68 ≠ 180. 2 $
Средняя часть трапеции:
Задача 6
Используйте теорему о среднем сегменте, чтобы определить длину включения среднего сегмента.
Длина среднего сегментаЧтобы вычислить длину среднего сегмента, найдите среднее значение длины оснований среднего сегмента = (6 + 4) / 2 = 5.
Быстрый обзор Midpoint
Самая важная вещь, о которой следует помнить, — это то, что средняя точка делит линию пополам (разрезает линию на две равные половины).
Показать среднюю точкуСредняя точка красного сегмента, изображенного ниже, — это точка $$ (A, 2b) $$ (нажмите кнопку ниже, чтобы увидеть).
Средний сегмент трапеции — это сегмент, соединяющий середины непараллельных сторон трапеции.
На трапеции ниже середины непараллельных сторон — это точки S и V. Средний сегмент — это красный отрезок линии от S до V.
Пример среднего сегмента
Трапеция # 10 Шаг 1 Расчет длины оснований. Верхняя база:$$ 35–16 = 9 $$
Шаг 2Расчет низкой базы:
$$ 45 — 0 = 45 $$
Шаг 3Расчет суммы оснований
$$ 9 + 45 = 54 $$
Шаг 4Разделите сумму на 2
$$ \ frac {54} {2} = \ boxed {27} $$
Проблема 8
Какова длина среднего сегмента SV трапеции ниже?
Показать ответ Шаг 1 Расчет длины оснований.Верхняя база:$$ 17–8 = 9 $$
Шаг 2Расчет низкой базы:
$$ 20 — 0 = 20 $$
Шаг 3Расчет суммы оснований
$$ 9 + 20 = 29 $$
Шаг 4Разделите сумму на 2
$$ \ frac {29} {2} = \ boxed {14.5} $$
Проблема 9
Красный сегмент ниже среднего сегмента?
Показать ответЭто не настоящий средний сегмент, потому что его длина не равна половине суммы длин оснований.
Иллюстративная математика
Задача
Ниже представлены изображения четырех четырехугольников: квадрата, прямоугольника, трапеции и параллелограмма.
Для каждого четырехугольника найдите и проведите все линии симметрии.
Комментарий IM
Это задание дает студентам возможность поэкспериментировать с отражениями плоскости и их воздействием на определенные типы четырехугольников.Это оба Интересно и важно, что эти типы четырехугольников можно отличить по линиям симметрии. С этой точки зрения здесь отсутствуют только изображения ромба и общего четырехугольника, которые не попадают ни в одну из рассматриваемых здесь специальных категорий.
Это задание лучше всего подходит для обучения, хотя его можно адаптировать для оценивания. Если учащиеся еще не выучили терминологию для трапеций и параллелограммов, учитель может начать с объяснения значения этих терминов.В пункте 4.G.2 говорится, что учащиеся должны классифицировать фигуры на основе наличия или отсутствия параллельных и перпендикулярных линий, поэтому эта задача будет хорошо работать в подразделении, отвечающем всем стандартам кластера 4.G.A.
Студенты должны сначала попытаться визуализировать линии симметрии, а затем они могут сделать или получить вырезы четырех четырехугольников или обвести их на кальке. Студентам полезно поэкспериментировать и увидеть, что идет не так, например, при отражении прямоугольника (который не является квадратом) по диагонали.Это упражнение помогает развить навыки визуализации, а также получить опыт работы с различными формами и их поведением при отражении.
Учащимся следует вернуться к этой задаче как в средней, так и в старшей школе, чтобы проанализировать ее с более сложной точки зрения по мере того, как они разрабатывают инструменты для этого. В восьмом классе четырехугольникам можно дать координаты, и ученики могут изучить свойства отражений в системе координат. В старших классах учащиеся могут использовать абстрактные определения отражений и различных четырехугольников, чтобы доказать, что эти четырехугольники на самом деле характеризуются количеством линий симметрии, которые у них есть.
Решение
Линии симметрии для каждого из четырех четырехугольников показаны ниже:
Когда геометрическая фигура складывается по линии симметрии, две половинки совпадают, поэтому, если у учащихся есть копии четырехугольников, они могут проверить линии симметрии, сложив их. Что касается квадрата, его можно сложить пополам по диагонали, горизонтальному сегменту, разрезающему квадрат пополам, или вертикальному сегменту, разрезающему квадрат пополам.Итак, у квадрата четыре линии симметрии. Прямоугольник их всего два, так как его можно сложить пополам по горизонтали или вертикали: учеников следует поощрять попытаться сложить прямоугольник пополам по диагонали, чтобы понять, почему это не работает. Трапеция имеет только вертикальную линию симметрии. У параллелограмма нет линий симметрии, и, как и в случае с прямоугольником, ученики должны поэкспериментировать со складыванием копии, чтобы увидеть, что происходит с линиями через диагонали, а также с горизонтальными и вертикальными линиями.
Указанные линии симметрии — единственные для фигур. Один из способов показать это — заметить, что для четырехугольника линия симметрии должна либо соответствовать двум вершинам на одной стороне линии с двумя вершинами на другой, либо проходить через две из вершин, а затем через две другие пары вершин. в сложенном виде по строчке. Это ограничивает количество возможных линий симметрии, и тогда эксперименты покажут, что единственно возможными являются те, которые показаны на рисунках.
бесплатных клипартов с трапециями, бесплатные клипарты с трапециями в формате PNG, бесплатные клипарты в библиотеке клипартов
трапеция черно-белый клипарт
штриховая графика
милые трапеции клипарт
как выглядит трапеция
трапеция четырехугольник
четырехугольная трапеция
трапеция
резиновое лобовое стекло cherokee xj
клипарт трапеция
симметрия
штриховая графика
картинки
трапеция малая
канцелярские товары
штриховая графика
шаблон колеса фортуны клин
трапеция картинки
иллюстрация
шестиугольник радуга
Диаграмматреугольник
трапеция вектор
абажур
розовый трапеция клипарт
белая трапеция png
форма клип арт
трапеция клипарт
геометрия клипарт
четырехугольная мозаика
десятисторонняя форма png
фигур картинки черно-белые
журнальный столик
размеров трапеции
трапеция черно-белая
картинки
Диаграммаобучение лидерству
бесплатных выкройки для квилтинга
журнальный столик
трапециевидный стол клипарт
лейтенант горн svg
прямоугольная форма клипарт
женский рождественский эльф картинки
штриховая графика
техасский логотип A&M Star
сохранять спокойствие
милые фигуры клипарт
милый рождественский баннер клипарт
трапеция клипарт
трапеция клипарт
трапеции картинки
контур трапеции
трапеция правая клипарт
Калькулятор трапеций: найдите A и P
Добро пожаловать в калькулятор трапеций Omni , где мы узнаем все об этих четырехсторонних формах.Мы покажем вам , как вычислить площадь трапеции, , как найти высоту трапеции, или как выглядит формула периметра трапеции . Также мы уделим время описанию некоторых особых типов четырехугольника: равнобедренной трапеции и правой трапеции. И не волнуйтесь; мы не оставляем камня на камне — мы даже упоминаем в калькуляторе срединный и трапециевидный углы.
Похоже, есть несколько вещей, которые нужно обсудить, так что приступим, ладно?
Что такое трапеция?
Трапеция — это четырехугольник (форма с четырьмя сторонами), у которого есть по крайней мере одна пара противоположных сторон, параллельных друг другу.Обратите внимание, что мы сказали «, по крайней мере, одна пара сторон» — если фигура имеет две такие пары, это просто прямоугольник. И не заблуждайтесь — каждый прямоугольник — это трапеция . Обратное, конечно, неверно.
Две параллельные стороны обычно называются основаниями . Обычно мы рисуем трапеции так, как мы делали выше, что может подсказывать, почему мы часто проводим различие между ними, говоря: нижнее и верхнее основание . Две другие непараллельные стороны называются ножками (аналогично двум сторонам прямоугольного треугольника).
Есть несколько особых случаев трапеций, которые мы хотели бы здесь упомянуть.
Прямоугольник
Мы уже упоминали об этом в начале этого раздела — это трапеция, которая имеет две пары противоположных сторон, параллельных друг другу .Равнобедренная трапеция
Трапеция, ног которой имеют одинаковую длину (аналогично тому, как мы определяем равнобедренные треугольники).Правая трапеция
Трапеция, у которой одна нога перпендикулярна основанию .Во-первых, обратите внимание, что здесь нам требуется только одна из ног, чтобы удовлетворить этому условию — другая может или не может. Во-вторых, обратите внимание на то, что если нога перпендикулярна одному из оснований, то она автоматически перпендикулярна и другой, так как обе ноги параллельны.
Имея в виду эти особые случаи, внимательный взгляд может заметить, что прямоугольников удовлетворяют условиям 2 и 3 . Действительно, если бы кто-то не знал, что такое прямоугольник, мы могли бы просто сказать, что это равнобедренная трапеция, которая также является правой трапецией.Довольно причудливое определение по сравнению с обычным, но оно определенно заставляет нас звучать утонченно, не так ли?
Прежде чем мы перейдем к следующему разделу, позвольте нам упомянуть еще два линейных сегмента, которые есть у всех трапеций.
Высота трапеции — это расстояние между основаниями, то есть длина линии, соединяющей два , которая перпендикулярна обоим. Фактически, это значение имеет решающее значение, когда мы обсуждаем, как вычислить площадь трапеции, и поэтому получает отдельный отдельный раздел.
Медиана трапеции — это линия, соединяющая середины ног. Другими словами, учитывая приведенную выше картинку, это линия, разрезающая трапецию по горизонтали пополам . Он всегда параллелен основаниям и с обозначениями, как на рисунке, у нас есть медиана = (a + b) / 2 . Если вам интересно название, обязательно ознакомьтесь с калькулятором медианы Omni (примечание: он не касается трапеций).
Хорошо, мы достаточно хорошо узнали нашу форму ; мы даже видели одну формулу трапеции! Давайте сделаем еще один шаг и попробуем еще лучше разобраться в теме.Мы начинаем этот углубленный анализ с формулы периметра трапеции и ее внутренних углов .
Формула периметра трапеции и углы трапеции
Периметр многоугольника равен сумме длин его сторон . Для героя сегодняшней статьи история ничем не отличается. Используя обозначения, как на рисунке в первом разделе (и в калькуляторе трапеций), мы выводим формулу периметра трапеции как:
P = a + b + c + d .Довольно просто, не правда ли?
Далее, поговорим об углах .Как и в любом другом четырехугольнике, сумма углов трапеции составляет 360 градусов (или 2π радиан). Однако условие трапеции (т. Е. Наличие пары параллельных сторон) накладывает дополнительных свойств на отдельные из них. Если быть точным, пара углов вдоль одной из ножек — это дополнительные углы. Это означает, что их сумма должна равняться 180 градусов (или π радиан), что в обозначениях из рисунка в первом разделе означает:
α + 𝛾 = β + δ = 180 ° .Обратите внимание, что наш инструмент также упоминает углы в нижнем наборе переменных полей. Таким образом, он также может служить калькулятором угла трапеции, когда это числа, которые мы ищем. И действительно, они часто пригодятся — они играют важную роль , когда мы учимся определять высоту трапеции, а это, в свою очередь, появляется при изучении того, как вычислить площадь трапеции. Однако начнем с последнего вопроса.
Как рассчитать площадь трапеции
Давайте снова возьмем картинку из первого раздела, чтобы вам не приходилось пролистывать всю статью всякий раз, когда вы хотите вспомнить обозначения.
Площадь формулы трапеции имеет следующий вид:
A = (a + b) * h / 2 .Обратите внимание, что действительно, как мы уже упоминали несколько раз, очень важно знать, как найти высоту трапеции для вычисления ее площади. Кроме того, ноги никогда не фигурируют в уравнении. Конечно, они определяют форму нашего четырехугольника, но их длина используется только в формуле периметра трапеции, которую мы обсуждали в предыдущем разделе.
Наконец, давайте проясним, что по порядку операций не имеет значения, в какой момент мы делим на 2 в указанной выше области формулы трапеции.Мы можем либо сначала вычислить (a + b) * h , а затем разделить все это на 2 , либо сначала найти h / 2 , и только затем умножить его на (a + b) . Фактически, зоркий глаз заметит, что (a + b) / 2 — это медианы , упомянутой в первом разделе. Другими словами, в качестве альтернативы мы можем использовать формулу A = median * h , чтобы найти A .
Хорошо, мы научились вычислять площадь трапеции, и все это кажется простым, если мы предоставим нам все данные на пластине. Но что, если они этого не сделают? Базы достаточно простые, а как насчет х ? Что ж, пора посмотреть , как найти высоту трапеции.
Как найти высоту трапеции
Решающий факт, который мы используем для определения высоты трапеции, заключается в том, что — это отрезок прямой, перпендикулярный основанию . Это дает нам прямой угол в обеих конечных точках, что позволяет нам использовать прямоугольные треугольники. И первое, что приходит в голову, когда мы слышим фразу прямоугольный треугольник , это, конечно же, теорема Пифагора.
Давайте проведем линию от одной из верхних вершин , которая падает на нижнее основание a под углом 90 градусов. (Обратите внимание, как для тупых трапеций, подобных изображенной на правом рисунке выше, высота х выпадает за пределы формы, то есть на линии, содержащей a , а не саму a . Тем не менее, то, что мы описываем ниже, все еще остается в силе. для таких четырехугольников.) Длина этой линии равна высоте нашей трапеции, поэтому именно то, что мы ищем. Обратите внимание на то, как мы нарисовали линию , она образует прямоугольный треугольник с одной из сторон c или d (в зависимости от того, какую верхнюю вершину мы выбрали).
Если у нас есть длина ноги трапеции и мы можем вычислить другую сторону прямоугольного треугольника (например, e или f на картинке выше), то мы знаем, как найти высоту трапеции — воспользуемся теоремой Пифагора .Однако есть еще один способ его вычисления.
Если вы немного разбираетесь в тригонометрии, вы сможете найти высоту , используя внутренний угол трапеции . Чтобы быть точным, глядя на углы трапеции в нашем калькуляторе (то есть на обозначения на рисунке), мы можем использовать определение тригонометрических функций, чтобы написать:
h = c * sin (α) = d * sin (δ) ,, где sin — синусоидальная функция. На самом деле может случиться так, что угол равен 30 , 45 или 60 градусов, и в этом случае мы можем просто использовать свойства специальных прямоугольных треугольников с такими внутренними углами.
Наконец, отметим, что весь этот поиск h очень прост в особом случае — когда у нас есть , это правая трапеция . Тогда высота нашей трапеции — это просто нога, лежащая рядом с прямым углом. Обратите внимание, что в этом случае приведенная выше тригонометрическая формула все еще работает, поскольку sin (90 °) = 1 .
Уф, это было много теории . Пришло время использовать эти формулы трапеций и посмотреть , как на практике вычислить площадь и периметр трапеции .
Пример: использование калькулятора трапеций
Давайте посмотрим на , как найти площадь и периметр трапеции со сторонами и углами, обозначенными как в калькуляторе трапеций, и следующими данными:
a = 8 дюймов , b = 5 дюймов , d = 3 дюйма , α = 90 ° , δ = 45 ° .
Вроде не много, но давайте посмотрим, что мы можем здесь сделать . Однако во-первых, давайте заметим, что наш калькулятор трапеций может легко справиться с нашей проблемой даже с таким небольшим количеством информации.Действительно, если мы введем вышеуказанные числа в наш инструмент (обратите внимание, как мы можем переключиться на другие единицы, щелкнув по ним и выбрав подходящий из списка), заполнит все остальные поля . Например, в качестве калькулятора угла трапеции он будет использовать идентификаторы, упомянутые во втором разделе, для вычисления β и 𝛾 . Также обратите внимание, что мы можем дополнительно перейти в расширенный режим и увидеть длину медианы.
Если инструмент может это сделать, то сможем и мы! Давайте посмотрим, как вычислить площадь и периметр трапеции вручную.
Прежде всего, обратите внимание, что мы имеем дело с правой трапецией , так как α = 90 ° (фактически, у нас также есть β = 90 ° ). Это означает, что сторона c перпендикулярна основаниям и, следовательно, равна высоте c = h . Однако мы не знаем c , поэтому нам нужно будет найти еще .
Для этого нарисуйте высоту нашей трапеции , которая идет от вершины между b и d .Вместе с d и частью a , он образует прямоугольный треугольник . Более того, нам известен один из его углов — δ = 45 ° . Значит, это один из частных случаев — это половина квадрата. Следовательно, h равно нижней стороне треугольника, а d фактически является диагональю квадрата, что означает, что:
h = d / √2 = 3 дюйма / √2 = 1,5√2 дюйма ≈ 2,1213 дюйма
(последнее равенство получаем, рационализируя знаменатель).
Теперь у нас есть все необходимое , чтобы найти A . Вспомните из специального раздела, как рассчитать площадь трапеции, и используйте эту информацию для получения
A = (a + b) * h / 2 = (8 дюймов + 5 дюймов) * 1,5√2 дюйма / 2 = 9,75√2 дюйма² ≈ 13,789 дюйма² .
Мы также собрали все данные, чтобы найти P , поскольку c = h = 1,5√2 в . По формуле периметра трапеции из второго сечения получаем
P = a + b + c + d = 8 дюймов + 5 дюймов + 1.5√2 дюйма + 3 дюйма = 16 + 1,5√2 дюйма ≈ 18,12 дюйма .

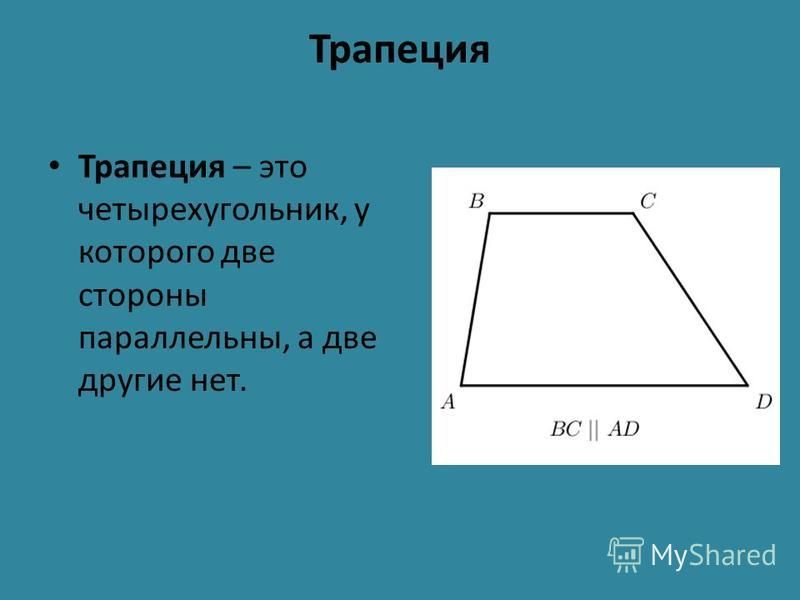

 Например, при изучении фигур повторяйте ещё и цвета: «Смотри, какой синий овал получился».
Например, при изучении фигур повторяйте ещё и цвета: «Смотри, какой синий овал получился».





